 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
|
De afgeleide van de cyclometrische
functies. |
| |
|
|
|
|
Om de afgeleide van de functies arcsinx en arccosx en
arctanx te vinden gaan we gebruik maken van het feit dat we hun
inversen goed kennen. Je weet natuurlijk al dat een functie en
zijn inverse elkaars gespiegelde zijn in de lijn y = x.
Laten we daarom eerst gaan kijken wat er met de afgeleide van een functie gebeurt
bij dat spiegelen. |
| |
|
|
|
|
|
| |
|
|
|
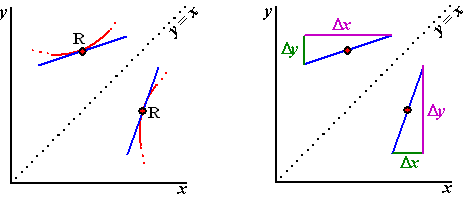
De rode grafiek in de linkerfiguur
wordt gespiegeld in de lijn y = x. De twee blauwe lijnen
zijn de raaklijnen in de punten R (die elkaars spiegelbeeld in y
= x zijn). In de rechterfiguur zie je die twee raaklijnen
nogmaals.
De bovenste raaklijn heeft helling
Δy/Δx
= groen/paars
en de onderste heeft helling
Δy/Δx
= paars/groen
Aan de lengte en kleur van die lijnstukjes zie je dat die twee
precies elkaars omgekeerde zijn; |
| |
|
|
|
| Bij
spiegelen in y = x wordt de helling het omgekeerde |
|
| |
|
|
|
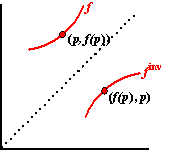
Zie de figuur
hiernaast.
Op de grafiek van f ligt een punt (p, f(p)),
en de helling is daar gelijk aan f '(p)
Dan ligt op de grafiek van finv een punt (f(p),
p) en de helling is daar gelijk aan 1/f
'(p)
We willen graag de helling is dat punt als functie van de x
daar, dus als functie van f(p)
Dus als het ons lukt om die helling 1/f '(p)te
schrijven als functie van f(p) dan zijn we klaar. |
 |
| |
|
probeer 1/f
'(x) te gaan schrijven als functie
van f(x) |
|
| |
|
|
|
Vertrouwd
voorbeeldje.
We weten dat de afgeleide van x2 gelijk is aan 2x,
en dat de inverse van x2 gelijk is aan
√x
Stel dat we de afgeleide van √x
niet zouden weten.....
• Op de grafiek van x2 ligt een punt (p,
p2) met helling 2p
• Dan ligt op de grafiek van √x
een punt (p2, p) met
helling 1/2p
• Probeer die 1/2p ook in termen van
p2 te schrijven, want dat is de x in dat
punt.
• Dat kan makkelijk: 2p = 2√(p2)
dus de helling in het punt waar x = p2 is
gelijk aan 1/2√(p2)
dus dat is 1/2√x
• Dus de afgeleide van √x
is 1/2√x
. |
| |
|
|
|
De afgeleide van arcsinx
Dat gaat op precies dezelfde manier als in het voorbeeldje hierboven. Ik
zal het regel voor regel kopiëren.
• We weten dat de afgeleide van sinx gelijk is aan cosx,
en dat de inverse van sinx gelijk is aan
arcsinx
• Op de grafiek van sinx ligt een punt (p,
sinp) met helling cosp
• Dan ligt op de grafiek van
arcsinx een punt (sinp, p)
met helling 1/cosp
• Probeer die 1/cosp ook in
termen van sinp te schrijven, want dat is de x in
dat punt.
• Dat kan: cosp =
√(1 - sin2p),
dus de helling in het punt waar x = sinp is gelijk aan
1/√(1 -
sin2p) dus dat is 1/√(1
- x2)
• Dus de afgeleide van arcsinx
is 1/√(1
- x2) . |
| |
|
|
|
|
De afgeleide van arccosx
|
| |
|
|
|
Nóg maar een keer
dan:
• We weten dat de afgeleide van cosx gelijk is aan -sinx,
en dat de inverse van cosx gelijk is aan
arccosx
• Op de grafiek van cosx ligt een punt (p,
cosp) met helling -sinp
• Dan ligt op de grafiek van
arccosx een punt (cosp, p)
met helling 1/-sinp
• Probeer die 1/-sinp ook in
termen van cosp te schrijven, want dat is de x in
dat punt.
• Dat kan: sinp =
√(1 - cos2p),
dus de helling in het punt waar x = cosp is gelijk aan
-1/√(1 -
cos2p) dus dat is -1/√(1
- x2)
• Dus de afgeleide van arccosx
is -1/√(1
- x2) . |
| |
|
|
|
|
De afgeleide van arctanx
|
| |
|
|
|
Wegens succes
geprolongeerd:
• We weten dat de afgeleide van tanx gelijk is aan
tan2x + 1, en dat de inverse van tanx
gelijk is aan arctanx
• Op de grafiek van tanx ligt een punt (p,
tanp) met helling tan2p + 1
• Dan ligt op de grafiek van
arctanx een punt (tanp, p)
met helling 1/tan2p
+ 1
• Die 1/tan2p
+ 1 staat al netjes in termen van tanp. en dat is de x
in dat punt.
• Dus de afgeleide van arctanx
is 1/(x2
+ 1) . |
| |
|
|
|
|
|
| |
|
|
|
N.B.
Het kan ook met impliciet differentiëren; dat gaat misschien nog wel
sneller. Bijvoorbeeld voor afgeleide van arcsinx kun je dit
verzinnen:
y = arcsinx ⇒ siny
= x
Ga dat impliciet differentiëren: cosy dy =
dx ⇒ dy/dx
= 1/cosy
Maar cosy = √(1 -
sin2y) = √(1 -
x2) dus y' = 1/√(1
- x²)
(die laatste regel geldt
alleen omdat -π/2
< y < π/2
zodat cosy positief is) |
| |
|
|
|
| |
|
|
|
|
|
| 1. |
a. |
Geef de vergelijking van de raaklijn in het punt
(1/2,
1/6π)
aan de grafiek van arcsinx. |
| |
|
|
|
|
|
| |
b. |
Geef de vergelijking van de raaklijn in het punt
(1/2√2,
1/4π)
aan de grafiek van arccosx. |
| |
|
|
|
|
|
| |
c. |
Geef een vergelijking van de raaklijn in het
punt (√3,
1/3π)
aan de grafiek van arctanx. |
| |
|
|
|
|
|
| |
|
| 2. |
Hoe kun je aan de afgeleide van arctanx
zien dat de grafiek een horizontale asymptoot heeft? |
| |
|
|
|
|
|
| 3. |
Onderzoek algebraïsch of de grafieken van arcsinx
en arccosx en arctanx een buigpunt hebben. |
| |
|
|
|
|
|
| 4. |
Gegeven is de functie f(x) =
4x + cosx
De inverse daarvan is nogal lastig te bepalen....
Maar omdat je weet dat het punt (0, 1) op de grafiek van f ligt kun je van die onbekende inverse functie wél de helling bij
x = 1 berekenen.
Maak die berekening. |
| |
|
|
|
|
|
| |
|
|
|
|
|
| |
|
|
|
|
 |
|
©
h.hofstede (h.hofstede@hogeland.nl) |
| |
|
|
|
|
|
|