|
Webquest: Wet van Benford |
||||||
| Dit is een statistisch onderzoek waarin je grote series getallen gaat bewerken met Excel en een onderzoek gaat doen naar de begincijfers daarvan. | ||||||
| 1. Gegevenstabel. | ||||||
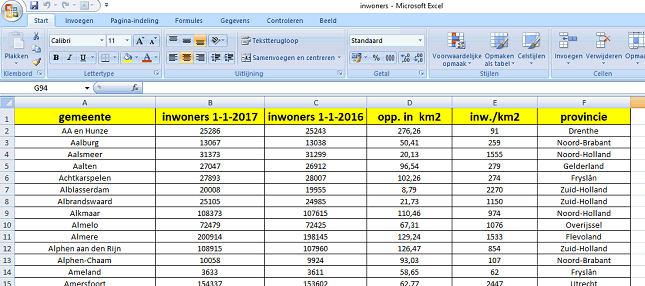
| Begin met het downloaden
van de inwoneraantallen in 2016 en 2017 en de oppervlakten van alle
388 Nederlandse gemeenten. Dat bestand kun je vinden op bevolkingbasisgemprov. Maak er een Excelbestand van dat er zó uitziet: |
||||||
|
|
||||||
| Zorg ervoor dat de kopteksten zichtbaar
blijven als je naar beneden scrollt. Het is handig om nu eerst alle hyperlinks te verwijderen. Dat doe je door alle cellen te selecteren (Ctrl A) en dan via de rechtermuisknop alle hyperlinks te verwijderen. |
||||||
| 2. Inwoners per provincie in 2017. | ||||||
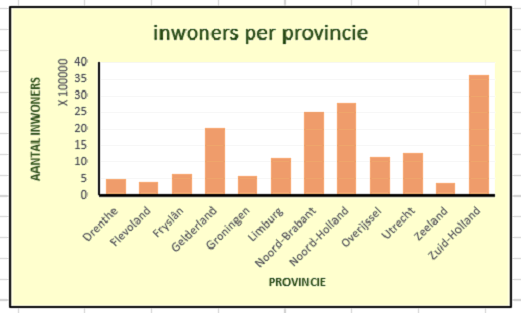
| We willen nu graag de
aantallen inwoners per provincie in een staafdiagram weergeven • Kopieer deze Exceltabel nu naar een blad 2 • Sorteer de gegevens naar provincie. • Tel vervolgens alle inwoners per provincie in 2017. Maak daarmee op blad 2 het volgende staafdiagram: |
||||||
|
|
||||||
| 3. De oppervlakte van de gemeenten. | ||||||
| Kopieer blad1 nogmaals, nu naar blad3 en bereken daarin de volgende gegevens: | ||||||
| • | Bereken voor alle gemeenten hoeveel de
procentuele toename of afname in het aantal inwoners tussen 1-1-2016 en 1-1-2017 is, en zet die op volgorde van groot naar klein. Bereken nu of het gemiddelde van al deze toename/afnamen gelijk is aan de gemiddelde toename /afname van de hele bevolking van Nederland. Geef een verklaring. |
|||||
| • | Zoek op internet of in de Bosatlas de totale oppervlakte van Nederland op en controleer of die gelijk is aan de oppervlakten van alle gemeenten samen. | |||||
| • | Bereken van het aantal inwoners per km2 van de gemeenten het gemiddelde en de standaarddeviatie. Leg uit wat deze getallen over de verdeling van het gemiddelde aantal inwoners per km2 zeggen. | |||||
| 4. De begincijfers. | ||||||
| Omdat die aantallen
inwoners vrij willekeurig zijn ontstaan zou je verwachten dat de
begincijfers ervan (1 tm 9) allemaal wel ongeveer even vaak zouden
voorkomen. Maar dat is niet zo! We gaan dat testen voor de begincijfers van de inwoneraantallen van 2016. Kopieer blad 1 naar een nieuw blad 4. En verberg alle kolommen behalve kolom C (aantallen 2016) Om het begincijfer van een getal in cel X te berekenen kun je de volgende formule gebruiken:
Zet deze formule maar eens in cel G2 en vervang X nu door C2 en je ziet dat er inderdaad een 2 verschijnt (het eerste cijfer van 25243 is immers een 2). |
||||||
| Zet op deze manier alle
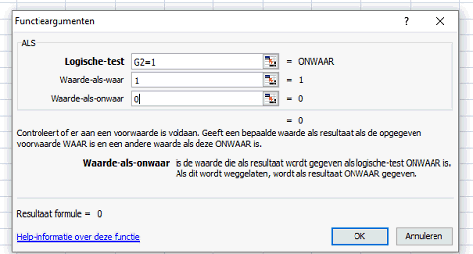
begincijfers van kolom C in kolom G. Nu willen we graag tellen hoeveel enen daar in kolom G staan. Natuurlijk ga je dat niet met de hand tellen, maar laat je Excel dat doen. Ga in cel H2 staan en toets in: • tabblad formules - logisch - ALS dan zie je dit: |
||||||
|
|
||||||
| • Bij logische test
vul je in G2 = 1 want je wilt immers testen of er een 1 staat
in cel G2 • Waarde-als-waar wordt een 1 • Waarde-als-onwaar wordt een 0 Nu komt er in H2 een 1 te staan als cel G2 een 1 bevat en in de andere gevallen een 0. Sleep H2 naar beneden en overal verschijnt een 1 als de G-kolom een 1 is. De enen kun je vervolgens makkelijk onderaan kolom H bij elkaar optellen (het worden er 124) In de kolommen I, J, K, L, M, N, O, P
kun je vervolgens op dezelfde manier gaan testen hoeveel keer het
getal 2, 3, 4, 5, 6, 7, 8, 9 in kolom G staat. |
||||||
|
|
||||||
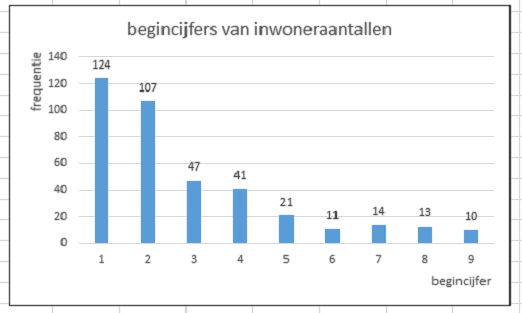
| Je ziet dat de begincijfers
helemaal niet even vaak voorkomen! Hûh?.......Wonderbaarlijk!! |
||||||
| 5. De wet van Benford |
 |
|||||
| Dit aparte verschijnsel,
dat het begincijfer 1 het vaakst voorkomt, daarna 2, daarna 3, enz. heet de
"Wet van Benford". Zoek op internet informatie over deze wet. Hieronder vind je een paar nuttige sites daarvoor: |
||||||
| https://wetenschap.infonu.nl/wiskunde/158698-de-wet-van-benford-een-inleiding.html | ||||||
| https://www.inzichten.nl/wetenschap/weten_50.htm | ||||||
| https://www.nemokennislink.nl/publicaties/1-aan-de-top/ | ||||||
| http://users.skynet.be/denkendehanden/benford.html | ||||||
| Schrijf een kort stukje over deze wet in een WORD bestand. Controleer of de theoretische frequenties van de begincijfers 1 tm 9 overeenkomen met de door jou gevonden frequenties bij onderdeel 4. | ||||||
| 6.
Eigen onderzoek. Sla dit onderdeel eerst over als je denkt in tijdnood te komen! |
||||||
| Als je werkblad 4 nu kopieert naar een werkblad 5, dan kun je kolom C vervangen door een andere serie meetgegevens, en daarmee direct weer de wet van Benford controleren. Doe dat op één van deze manieren: | ||||||
| 1. | Kies de rij getallen 2-4-8-16-32-64-..... in kolom C. Neem minstens 100 getallen. | |||||
| 2. | Zoek op internet een serie getallen en kopieer die naar kolom C. | |||||
| Je mag natuurlijk ook beiden doen......J | ||||||
| 7. Een toepassing. | ||||||
| Lees eerst het volgende artikel: https://www.inzichten.nl/wetenschap/weten_52.htm | ||||||
| In
dit bestand
vind je twee begrotingen van twee schoolbesturen (A en B). Als één van beiden fraude pleegt met de begroting, welk schoolbestuur zou dat dan volgens de wet van Benford het meest waarschijnlijk zijn? Gebruik weer je excel-blad4, en kopieer dat naar blad6 en blad7. |
||||||
| 8. Afsluitend. | ||||||
| Lever je Excel-bestand en je Word-bestand in bij je leraar. | ||||||