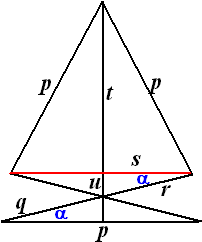
|
cosa = (0,5p)/q
Þ q = p/(2cosa)
Þ r
= p - q = p • (1 - 1/(2cosa))
cosa = s/r
Þ s =
r • cosa = cosa • p • (1 - 1/(2cosa))
Pythagoras: t2 = p2 - s2
Þ t = Ö(p2 - cos2a • p2
• (1 - 1/(2cosa))2)Pythagoras: u2 = r2 - s2
Þ u = Ö(p2 • (1 - 1/(2cosa))2 - cos2a
• p2 • (1 - 1/(2cosa))2)
Þ u= Ö( (1 - cos2a)
• p2 • (1 - 1/(2cosa))2)
Þ u = sina • p
• (1 - 1/(2cosa)) u
+ t = p Þ sina
• (1 - 1/(2cosa))
+ Ö(1 - cos2a
• (1 - 1/(2cosa))2)
= 1 |
 |
|
|
Nu wordt het mij te machtig...
Dus grijp ik mijn TI-83, en vind: a
= 14,023521º of a
= 60º
Gelukkig maar, a = 60º
geeft de "ontaarde" oplossing dat de bovenste drie lucifers
rechtop staan en over elkaar liggen.
De gezochte a is dus de
eerste, en invullen geeft r =
0,48464... |
|
|
|
|