|
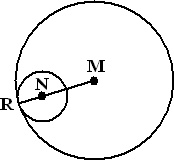
Eerst gebruiken we de
eigenschap dat, als een cirkel raakt aan een andere, dat
dan de lijn door het raakpunt en het middelpunt van de ene
cirkel ook door het middelpunt van de andere cirkel gaat.
Dat moet wel, want deze lijn staat loodrecht op de
raaklijn in R, en dat staan de lijnen vanuit de
middelpunten ook. |
 |
|
|
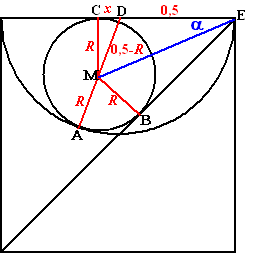
Dat betekent in de figuur
hiernaast dat als we AM verlengen, dat die lijn dan door D
(het middelpunt van de halve cirkel) gaat.
DA = straal halve cirkel = 0,5 (stel de zijde van het
vierkant 1)
Stel de straal van de cirkel R
Dan is MD = 0,5 - R
Pythagoras in CDM: R2 + x2 =
(0,5-R)2
Dat geeft na uitwerken x
= Ö(0,25 - R)
.......(1)
Nu het raakpunt B nog gebruiken (de diagonaal dus)
Ða = 22,5º
Omdat tan 45º = 1, kunnen we deze verdubbelingsformule
handig gebruiken:
|
 |
Met b
= 22,5º geeft dat 1- tan2b
= 2tanb
Daaruit volgt tanb = -1 +
Ö2 (met de
ABC-formule)
driehoek MCE geeft dan -1 + Ö2
= R/(x+ 0,5)
Dat geeft met de eerder gevonden formule (1)
voor x: (-1 + Ö2)•(Ö(0,25
- R) + 0,5) = R
Þ (-1 + Ö2)•(Ö(0,25
- R) = R - (-1 + Ö2)•0,5
Nu kwadrateren: (3-2Ö2)•(0,25
- R) = R2 + R - RÖ2
+ 0,75 - 0,5Ö2
Herrangschikken en alles naar één kant: R
• (R + 4 - 3Ö2) = 0
Conclusie: R = 3Ö2
- 4 |
|
|
| En nu de tweede
nog...... |
|
|
|
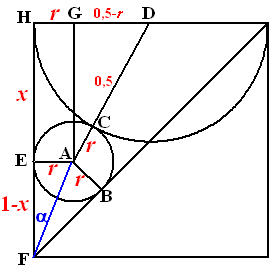
Die is gelukkig makkelijker.
In driehoek AGD: (0,5 - r)2 + x2 =
(0,5 + r)2
Daaruit volgt x = Ö(2r)
Dus EF = 1 - Ö(2r)
In driehoek FAE: tan a
= -1 + Ö2 = r/(1
- x)
Dus (-1 + Ö2)•(1
- Ö(2r)) = r
-1 + Ö2 +
Ö(2r)
- 2Ör = r
Þ
r +
Ör • (2 - Ö2)
+ (1 - Ö2) = 0
kwadraat afsplitsen:
(Ör + 1 - 0,5Ö2)2
- (1 - 0,5Ö2)2 +
(1 - Ö2) = 0
Þ (Ör
+ 1 - 0,5Ö2)2 =
0,5
Þ Ör
+ 1 - 0,5Ö2 = Ö0,5
Þ Ör
= 0,5Ö2 - 1 + 0,5Ö2
= Ö2 - 1
Þ r = (Ö2
- 1)2 = 3 - 2Ö2
r = 3 - 2Ö2 |
 |
|
|
|
|