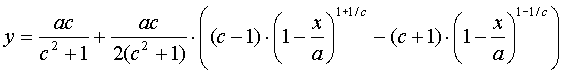Dit is ons probleem als we m = a substitueren:
![]()
Deze vergelijking is gelukkig separabel:
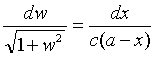
Het eerste probleem is de primitieve van het linkerlid te vinden.
Oké; ik geef het toe: hier kwam ik niet uit.
Ik heb het (tot mijn schande) in een tabel moeten opzoeken.
De primitieve van het linkerlid is ln(w + Ö(1 + w2))
Primitiveren geeft dan:
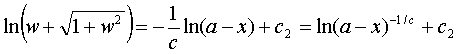
Ik
ben overal nogal slordig met absolute waardes; alles is gewoon groter dan nul,
controleer dat zelf maar.
c2 is een integratieconstante.
Beide kanten de exponent nemen:
![]()
De voorwaarde w = 0, x = 0 levert de waarde van
c3
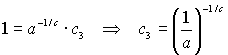
Substitueren in de vergelijking:
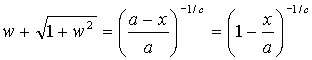
Breng nu w naar de andere kant, en kwadrateer beide zijden; dat
geeft:
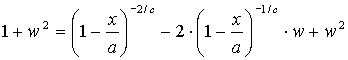
De termen w2 vallen tegen elkaar weg. Laten we vervolgens w
gaan isoleren:
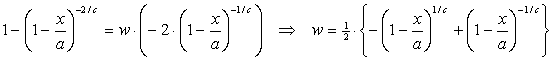
Maar bedenk dat w = dy/dx.
Dus laten we wéér primitiveren:
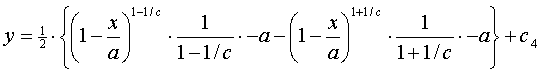
De factor -a komt van de kettingregel, c4 is weer
een integratieconstante.
Bedenk dat 1 - 1/c = (c -
1)/c en dat
1 + 1/c = (c + 1)/c. Herrangschikken geeft dan:
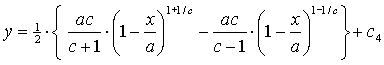
Tussen accolades vermenigvuldigen we nu de eerste term met (c-1)/(c-1) en de
tweede met (c+1)/(c+1)
Dat geeft:
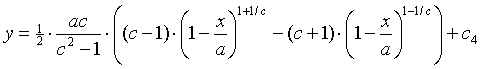
Nu c4 nog: we weten dat als x = 0 dat y =
0. Invullen geeft:
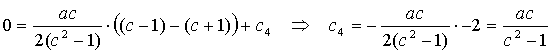
En
ja hoor, daar is 't ie dan: