OK, voor de echte die-hards dan. Stroop de mouwen maar op, daar gaan we:

Definieer u = ^y/_x  dus  y =  u • x
Dan is dy = du • x + u • dx   (productregel)
Substitueren in de differentiaalvergelijking geeft:

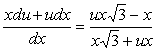Kruislings vermenigvuldigen en hergroeperen:

(xdu + udx)•(xÖ3 + ux) = dx • (uxÖ3 - x)
Þ  x²Ö3du + x²udu + uxÖ3dx + u²xdx =  uxÖ3dx - xdx
Þ   x²Ö3du + x²udu  + u²xdx =  - xdx
Þ   xÖ3du + xudu  + u²dx =  - dx
Þ   xdu•(Ö3 + u) = dx•(-1 - u²)

Nu zijn de u's en de x-en van elkaar te scheiden, en dan kunnen we beide kanten primitiveren:

-Ö3•arctan(u) - ¹/₂ln(1 + u²) = ln x + c
Þ  -Ö3•arctan(u)  = ¹/₂ln(1 + u²) + ln x + c
Þ  -Ö3•arctan(u) = ln(1 + u²)^½ + ln x + c
Þ  -Ö3•arctan(u) = ln {x•Ö(1 + u²)} + c

(waarbij gebruik gemaakt is van lna + lnb = lnab  en  k • lna = ln a^k)
c is een integratieconstante.

Terug naar x en y:  bedenk dat  u = ^y/_x . Dat geeft:


Nu gaan we over op poolcoördinaten:  r = Ö(x² + y²)  en  a = arctan(^y/_x)
Het eindresultaat is verrassend eenvoudig: