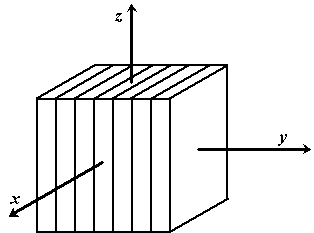
| We verdelen de kubus in 7 plakken van
breedte 1, en leggen meteen maar even een assenstelsel aan (met de
oorsprong precies midden in de grote kubus): |
Als we de hele kubus in 343
eenheidskubusjes verdelen, dan zijn de co÷rdinaten van de middelpunten
van die kubusjes precies de gehele getallen van -3 t.m. 3.
De som van alle y-co÷rdinaten van de middens van die kubusjes is
dan NUL (uit symmetrieoverwegingen)
|
 |
| Moeten we nu binnen deze grote kubus een
blokje van 3 eenheidskubusjes plaatsen dan zijn er twee mogelijkheden: |
|
| 1. |
Het 3-blokje ligt geheel binnen ÚÚn van de zeven
plakken van de kubus. |
| 2. |
Het 3-blokje gaat door drie plakken heen. |
|
|
|
| |
| Voor de y-co÷rdinaten van de
kubusjes van zo'n 3-blokje zijn er dan ook twee mogelijkheden: |
| 1. |
de y -co÷rdinaten zijn alle drie gelijk. |
| 2. |
De y-co÷rdinaten zijn drie opeenvolgende gehele
getallen. |
|
|
|
| |
In beide gevallen is de som van de drie y-co÷rdinaten
gelijk aan 0 (mod 3)
JAWEL! Daar is weer zo'n Beschrijvende
functie!
..... Dus de som van ALLE y-co÷rdinaten van alle 3-blokjes is
ˇˇk 0 (mod 3)
..... Maar de som van alle y- co÷rdinaten van alle blokjes
(inclusief het GAT) was ˇˇk 0
Dus moet de y-co÷rdinaat van het GAT ook wel gelijk zijn
aan 0 (mod 3), dus -3 of 0 of 3.
-3 en 3 vallen af, want die zitten aan het oppervlak.
CONCLUSIE: de y-co÷rdinaat van het GAT is 0.
Op precies dezelfde manier kunnen we concluderen dat ook de x-
en de z - co÷rdinaat van het GAT gelijk moeten zijn aan 0.
Dus GAT = (0,0,0) |
|
|
|