|
Gietproblemen |
|
| Op een verrassende manier lijkt
dit probleem op een stuiterbal die in een isometrisch rooster heen en
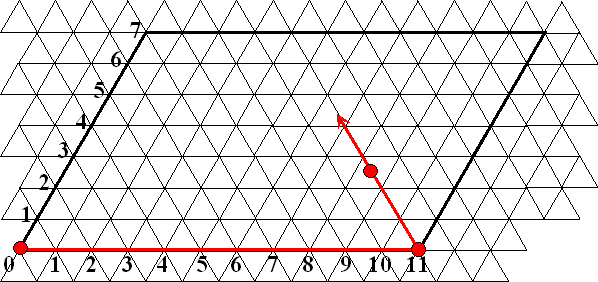
weer gaat. Omdat onze flessen 11 en 7 liter zijn tekenen we een parallellogram van
11 bij 7: |
|
 |
|
Een bal begint in de oorsprong
((0,0): alles leeg) naar rechts te rollen. Hij stuitert in (11,0) tegen
de zijwand. Dat correspondeert met vaas 11 vol en 7 leeg. Daarna reist
de bal van (11,0) schuin naar de bovenkant. Deze reis symboliseert het
leeggieten van de vaas van 11 in de vaas van 7.
De bal zal de bovenkant raken in (4,7) hetgeen overeenkomt met de
vaas van 7 vol, en 4 liter in die van 11.
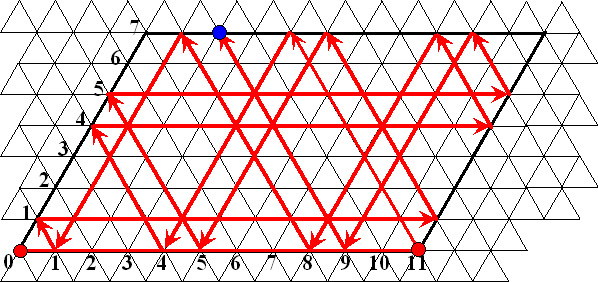
En zo blijft de bal heen en weer stuiteren tot hij ergens aan een kant
het getal 2 raakt: |
|
 |
|
|
| De oplossing staat hierboven getekend in het
rooster en komt overeen met de volgende 18-staps oplossing:
|
|
|

|
| |
|
Natuurlijk kun je ook beginnen met het balletje
omhoog te laten rollen. Dat geeft de volgende 15-staps
oplossing:
(0,0)(0,7)(7,0)(7,7)(11,3)(0,3)(3,0)(3,7)(10,0)(10,7)(11,6)(0,6)(6,0)(6,7)(11,2) |
| |
In de eerste oplossing vul je
steeds het 11 liter vat, en leegt dat in het 7 liter vat. Elke keer als
het 7-litervat vol is leeg je het weer. Dat komt eigenlijk neer op het
zoeken naar oplossingen van de vergelijking 7x + 11y =
2
Een oplossing is bijvoorbeeld x= -6 en y = 4
en dat vertalen we naar "Vul het 11-liter vat 4 keer en leeg het
steeds in het 7-litervat. Gooi het 7-litervat 6 keer leeg (steeds als
het helemaal vol is)"
Algemene andere oplossingen zijn: x = -6 + 11k
en y = 4 - 7k
Voor k = 1 vinden we x = 5 en y = -3
en dat betekent "Vul het 7-litervat 5 keer en leeg het steeds in
het 11-litervat. Gooi het 11-litervat 3 keer leeg (steeds als het
helemaal vol is)"
Dit zijn precies de twee hierboven gevonden oplossingen. |
| |
Uitbreiding
Wat verandert er als we niet twee
vazen en een groot reservoir hebben, maar drie vazen waarvan de grootste
gevuld is? Dat kunnen we ook grafisch weergeven door voor de kleinste
twee vazen een parallellogram te tekenen en daarbij een extra lijn
evenwijdig aan een hoofddiagonaal die de derde vaas voorstelt.
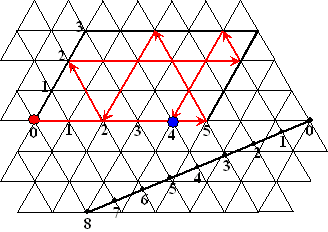
Hieronder staat de 7-staps oplossing voor drie vazen van 3, 5 en 8
liter, waarmee tweemaal 4 liter gemaakt moet worden:
Op de diagonaal kun je aflezen
hoeveel er steeds in de 8-liter vaas zit.
De oplossing is dus
(0,0,8)(5,0,3)(2,3,3)(2,0,6)(0,2,6)(5,2,1)(4,3,1)(4,0,4) |
 |
|
| |
| Er zijn twee dingen die fout
kunnen lopen. |
- Ten eerste kan de bal op een gegeven moment gaan rondstuiteren
over steeds dezelfde route terwijl nog niet alle punten zijn
bereikt. Dat is zo als de kleinste twee vazen een gemeenschappelijke
deler hebben. (dat staat hieronder voor vazen van 3, 6 en 9 liter.
- Ten tweede gaat het mis als de grootste vaas kleiner is dan de
andere twee samen. Stel dat de 8-liter vaas slechts 6 liter was. Dan
moeten we een stuk van het parallellogram afsnijden:
|
| |
In beide gevallen gaat de bal
'rondjes draaien' en zijn niet alle hoeveelheden af te meten.
Maar in alle andere gevallen is elke hoeveelheid, die kleiner dan of
gelijk aan de middelste vaas is, af te meten.
Met vazen van bijv. 21, 22, en 43 liter zijn alle
hoeveelheden 0,1,2,3,...,21 af te meten. |
|