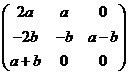1.	In R3 zijn ten opzichte van een orthonormale basis gegeven het vlak V met vergelijking 2x1 + x2 - 2x3 = 0
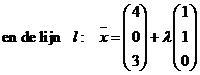	a.	Bereken de afstand van l en de x3-as.
	b.	A is een punt van l  en B is een punt van de x3-as. De lijn AB is evenwijdig aan vlak V. M is het midden van het lijnstuk AB. Stel een vectorvoorstelling op van de punten M.
	c.	Een vlak W door l maakt met V een hoek van 45º . Stel een vergelijking van W op.
2.	In R3 is ten opzichte van een orthonormale basis gegeven het vlak V met vergelijking 2x1 + x2 + x3 = 0, en voor elke (a, b) ∈ R × R de afbeelding Aa,b  met matrix:
	a.	Voor welke p ∈ R  behoort (p - 1, 0, p) tot het A1,2-beeld van V?
	b.	Voor welke a is Aa,1 een singuliere afbeelding?
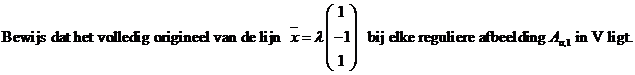	c.	Het vlak met vergelijking x3 = 0  wordt door Aa,b afgebeeld op een lijn l in dat vlak waarbij de punten van l invariant zijn. Bereken a en b.
3.	In R3 zijn ten opzichte van ene orthonormale basis gegeven de punten O(0,0,0), P(4,4,0), Q(0,4,0) en R(2,2,4). A is een spiegeling in het vlak OPR en B is een spiegeling in het vlak OQR.
	a.
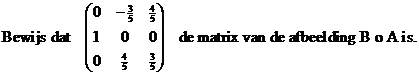	b.	Gegeven is dat de afbeelding B o A een draaiing is om een lijn over een hoek φ. Stel een vectorvoorstelling van deze lijn op en bereken cos φ.
	c.
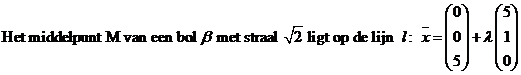		β β

UITWERKING
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.