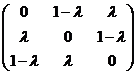1.	In R3 is ten opzichte van een orthonormale basis voor elke λ ∈ R de lineaire afbeelding Al gegeven met matrix:
	a.	Toon aan dat de afbeelding Al regulier is voor elke  λ ∈ R.
	b.	Toon aan dat precies twee van de afbeeldingen Al orthogonale afbeeldingen zijn.
	c.	Bewijs dat voor elke x ∈ R3 en voor elke λ ∈ R de punten A0(x), A1(x) en Al(x)  op één rechte lijn liggen
	d.	Voor welke λ geldt dat voor alle x ∈ R3    | Aλ(x) | = | A3(x) |   ?
2.	In R3 zijn t.o.v. een orthonormale basis gegeven de lijnen:
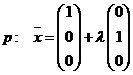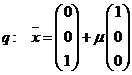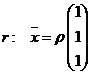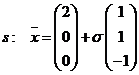	Verder is V de verzameling punten die gelijke afstand hebben tot de lijnen p en q.
	a.	Toon aan dat een vergelijking van de verzameling V is:  x12 - x22 = 2(x1 - x2)
	b.	Toon aan dat de doorsnede van V met het vlak met vergelijking x1 + x2 = 2 een rechte lijn is.
	c.	Toon aan dat de lijnen r en s deelverzamelingen van V zijn.
	d.	Bewijs dat iedere rechte lijn die r en s snijdt en evenwijdig is aan het vlak met vergelijking x1 + x2 = 0 een deelverzameling van V is.
3.
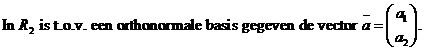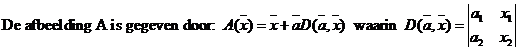	a.	Bewijs dat A een lineaire afbeelding is.
	b.	Bewijs dat A een reguliere afbeelding is.
	c.
	d.

UITWERKING
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.