| 1. | Gegeven zijn de
punten O(0,0,0), A(1,0,0), C(0,1,0) en D(0,0,1). Deze punten zijn de hoekpunten van de kubus OABC.DEFG. Het midden van de ribbe BF is M. |
||
| a. | Een lijn l
door O die in het vlak x3 = 0 ligt, maakt
gelijke hoeken met de lijnen CM en EM. Stel een vectorvoorstelling op van l |
||
| b. | Kies een punt van lijn AF. Bereken de co÷rdinaten van K, als de oppervlakte van driehoek BGK minimaal is. | ||
| c. | Vlak V gaat door
O en snijdt de lijnen DG, DM en DA achtereenvolgens in de punten P.
Q en R. Vierhoek PQRO is een parallellogram. Stel een vergelijking van het vlak V op. |
||
| 2. | Gegeven zijn de
punten O(0,0,0), A(4,0,0), B(0,1,0), C(0,0,4), D(0,4,8) en
E(8,0,4) De afbeelding P is de loodrechte projectie op het vlak BEO. De afbeelding Rφ is de rotatie om de lijn OB over een hoek φ zodat A het beeld is van C als φ = 1/2π. |
||
| a. | Stel de matrix op van de afbeelding P. | ||
| b. | Onder de afbeelding Rπ/2 o P heeft de lijn DE een beeld. Stel een vectorvoorstelling op van dit beeld van DE. | ||
| c. | Bewijs dat de kern van de afbeelding Rj o P onafhankelijk is van φ. | ||
| d. | Een bol
β gaat door C, raakt de lijn DE in D en raakt
het vlak BEO. Stel een vergelijking op van β. |
||
| 3. |
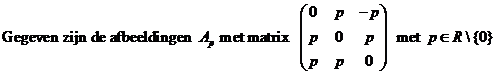 |
||
| a. | Bewijs dat voor elke p de afbeelding Ap singulier is. | ||
| b. | Wat is bij variabele p de verzameling van de beelden van het punt (1, 2, 1) onder de afbeelding Ap? | ||
| c. | Voor welke p en voor welke x ≠ 0 geldt Ap(x) = x | ||
| d. | Welke vlakken
hebben bij elke Ap hetzelfde volledige origineel als
het vlak x1+ x2 + x3
= 0 ? N.B. Bij een afbeelding is het volledige origineel van een verzameling V de verzameling van alle originelen van de elementen van V. |
||