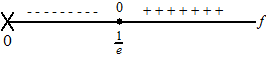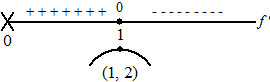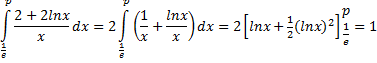1.
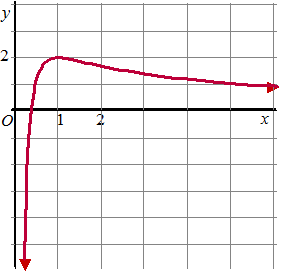
	a.	Onderzoek f en teken de grafiek van f Bereken de coördinaten van het buigpunt van de grafiek van f.
	b.	De raaklijn in een punt P aan de grafiek van f gaat door de oorsprong (0,0) Bereken de coördinaten van P.
	c.	De oppervlakte van het gesloten vlakdeel, begrensd door de grafiek van f, de x-as en de lijn x = p is gelijk aan 1 Bereken p.
2.	Gegeven is de differentiaalvergelijking  xdy - 3ydx = u(x)dx, waarbij u een op R gedefinieerde, differentieerbare functie is.
	a.	Voor welke functies u geldt dat y = u(x) een oplossing van de differentiaalvergelijking is?
	b.	Als de functie f een oplossing van de differentiaalvergelijking is, dan is voor elke c ∈ R de functie  g:  x →  f(x) + cx3 ook een oplossing van de differentiaalvergelijking. Bewijs dit.
	c.	Neem u(x) = 6x. De verzameling van de punten waarvan het door de differentiaalvergelijking gedefinieerde lijnelement een richtingscoëfficiënt p heeft, is een integraalkromme van de differentiaalvergelijking. Bereken p.
3.	De kromme K is gegeven door:  x = t2  en  y = t2 • e1 - t
	a.	De lijn x = 1 snijdt K in de punten A en B Bereken de richtingscoëfficiënt van de raaklijn in A en die van de raaklijn in B aan de kromme.
	b.	Voor welke a heeft de lijn y = ax slechts één punt met K gemeen?
	c.	In welk punt van K is de raaklijn evenwijdig aan de x-as? Stel een vergelijking op van de asymptoot van K. Teken K.
4.	De functie f van [1/2π, 11/2π] naar R is gegeven door f :  x → √(1 - sinx)
	a.	Los op:  f(x) = sinx + cosx
	b.	Bereken de richtingscoëfficiënt van de raaklijn in het punt (1/2π, 0) aan de grafiek van f.
	c.	Op de grafiek van f  ligt een punt P met x-coördinaat p. De lijn door P, loodrecht op de raaklijn aan de grafiek van f in P, snijdt de x-as in punt A. De projectie van P op de x-as is punt B. Bewijs dat de x-coördinaat van A is  p - 1/2cosp Bereken de maximale oppervlakte van driehoek ABP.
5.	Zes vrienden gaan naar een zeer druk bezochte hondententoonstelling. Ieder komt op eigen gelegenheid. Elke bezoeker ontvangt bij zijn binnenkomst een enveloppe. Eén op de drie enveloppen bevat een cadeaubon.
	a.	Bereken de kans dat precies twee van de zes vrienden een cadeaubon krijgen.
	De vrienden spreken af dat zij bij aankomst in de koffiekamer van het tentoonstellingsgebouw op elkaar zullen wachten. Twee van de zes vrienden zullen elk hun hond meenemen naar de tentoonstelling. X is het aantal honden van de vrienden dat gearriveerd is op het moment dat er nog maar vier vrienden aanwezig zijn.
	b.	Geef de kansverdeling van X, aangenomen dat de volgorde waarin de vrienden aankomen willekeurig is.
	Tijdens een koffiepauze vragen de vrienden zich af hoe groot de fractie f  is van het aantal bezoekers dat een hond naar de tentoonstelling heeft meegenomen. Zij beschouwen zichzelf voorlopig als representatief en veronderstellen f gelijk aan 1/3. Zij nemen een aselecte steekproef van 20 bezoekers, en besluiten hun veronderstelling te verwerpen als er onder deze 20 bezoekers hoogstens 3 of minstens 11 een hond hebben meegenomen.
	c.	Bereken de kans dat zijn hun veronderstelling ten onrechte zullen verwerpen.

UITWERKING
1a.	Domein:   á0, ®ñ  Nulpunten:  f(x) = 0   Þ  2 + 2lnx = 0   Ù   x ¹ 0 2lnx = -2  Ù   x ¹ 0 lnx = -1  Ù   x ¹ 0 x = e-1 = 1/e  Ù   x ¹ 0 Tekenbeeld van f:
	Afgeleide (met de quotiëntregel)
	f '(x) = 0    -2lnx = 0   Ù   x ¹ 0  Þ    x = 1, dus dit is het tekenbeeld van f ' :
	f(x) bereikt voor x = 1 een lokaal maximum van  y = 2
	Dus x = 0 is verticale asymptoot  en  y = 0 is horizontale asymptoot.  Dat geeft samen zo'n grafiek:
	Het bereik is   á-¥, 2]
1b.	y = ax  raakt de grafiek, dus dan is  f(x) = ax  en  f '(x) = a. -lnx/x² = a   geeft ax2 = -2lnx  ........(1) (2 + 2lnx)/x = ax  geeft  ax2 = 2 + 2lnx  .....(2) (1) en (2) samen geven:   -2lnx = 2 + 2lnx 2 = 4lnx lnx = 1/2 x = e0,5 = √e Dan is  y = (2 + 2 • 0,5)/√e  = 3/√e P = (√e , 3/√e)
1c.
	(lnp + 1/2ln2p) - (-1 + 1/2) = 1/2 lnp + 1/2ln2p  = 0 1/2lnp •  (2 + lnp) = 0 lnp = 0 Ú  lnp = -2 p = 1  Ú   p = e-2
2a.	xdy - 3ydx = u • dx y = u(x) is een oplossing:    xu' dx - 3udx = udx u ' = 4u u(x) = c • e4x
2b.	y = f(x) + cx3  invullen in  xdy - 3ydx x • (f ' dx + 3cx2dx) - 3(f + cx3)dx = xf ' dx + 3cx3dx - 3f dx - 3cx3dx   = xf ' dx  - 3f dx  = udx de laatste stap omdat f een oplossing is.
2c.	xdy - 3ydx = 6xdx  dy/dx = p geeft  dy = pdx  dus de vergelijking wordt dan  pxdx - 3ydx = 6xdx px - 3y = 6x y = (2 - 1/3p)x  Dat moet een integraalkromme zijn dus dat kun je invullen in de differentiaalvergelijking: x • (2 - 1/3p)dx - 3(2 - 1/3p)xdx = 6xdx (2 - 1/3p) - 3(2 - 1/3p) = 6 2 - 1/3p - 6 + p = 6 2/3p = 10 p = 15
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.