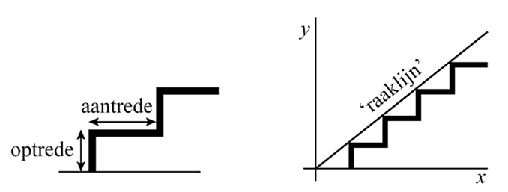| Eten buiten de deur. | |||
| Prijzen van
producten, waaronder die van voedsel, stijgen elk jaar met een bepaald
percentage. We noemen dat percentage inflatie. In 2020 werd een onderzoek naar de kosten van voedsel in de Verenigde Staten gepubliceerd. Volgens het onderzoek gaf in 1988 een gemiddelde Amerikaan $ 1143 per jaar uit aan eten thuis en steeg dit bedrag door inflatie tot $ 2079 in 2008. Neem aan dat tussen 1988 en 2008 de inflatie ieder jaar hetzelfde was. |
|||
| 3p. | 1. | Bereken deze inflatie. Geef je antwoord in procenten in twee decimalen. | |
| In het onderzoek
werd onderscheid gemaakt tussen eten thuis: voedsel dat thuis gegeten
wordt, en eten buiten de deur: voedsel dat elders wordt gegeten
(bijvoorbeeld in restaurants, onderweg of op het werk). We gaan er verder van uit dat vanaf 2010 de inflatie jaarlijks 2% was. Uit het onderzoek bleek dat vanaf 2010 de kosten voor eten buiten de deur inclusief de jaarlijkse inflatie ook nog stegen met een extra percentage van 0,84% per jaar. Op 1 januari 2010 betaalde je voor een Bacon Cheeseburger bij een bepaalde Amerikaanse fastfoodketen $ 4,25. |
|||
| 4p. | 2. | Bereken in welk jaar de prijs van dezelfde Bacon Cheeseburger volgens deze aannamen $ 7,00 zal zijn. | |
| In het onderzoek
werd ook gekeken naar de totale uitgaven voor voedsel (eten thuis plus
eten buiten de deur). Om deze uitgaven uit verschillende jaren met
elkaar te kunnen vergelijken, werden alle bedragen omgerekend naar
bedragen in 1988. Hierdoor hoeft er geen rekening gehouden te worden met
inflatie. De (naar 1988 omgerekende) uitgaven voor eten thuis blijken ieder jaar hetzelfde te zijn, namelijk $ 1143. We nemen aan dat dit de komende jaren zo zal blijven. De totale uitgaven voor voedsel per persoon, omgerekend naar de bedragen in 1988, namen lineair toe van $ 1600 in 1953 tot $ 2250 in 2014. |
|||
| 4p. | 3. | Bereken in welk jaar een gemiddelde Amerikaan voor het eerst meer uitgaf voor eten buiten de deur dan voor eten thuis. | |
| Goals in de Eredivisie | |||||||||||||||||
| De Eredivisie is de hoogste
voetbalafdeling in Nederland in de betaalde mannencompetitie. Aan
het einde van seizoen 2021/22 stond op een voetbalwebsite de
volgende uitspraak: “Zorgelijke trend: steeds minder goals in de Eredivisie.” Het gemiddelde aantal goals per wedstrijd lag in het seizoen 2021/22 op 2,8595. De competitie telde toen 306 wedstrijden. In het seizoen 1965/66 werden er 779 goals gescoord. Er werden toen 240 wedstrijden gespeeld. Op basis van deze gegevens is er een argument te geven waarbij je het eens bent met de uitspraak op de website en is er ook een argument te geven waarbij je het oneens bent met de uitspraak. |
|||||||||||||||||
| 2p. | 4. | Geef bij beide argumenten een berekening die het argument ondersteunt. | |||||||||||||||
| In de
Eredivisie wordt een volledige competitie gespeeld. Dit betekent dat
elk team twee keer tegen elk ander team speelt – één keer thuis en
één keer uit. Het totaal aantal wedstrijden in de volledige
competitie noemen we W en het aantal teams in de competitie
T. Uit deze gegevens is af te leiden dat: W =
T2 - T In de seizoenen 1962/63 tot en met 1965/66 waren er minder teams en minder gespeelde wedstrijden dan tegenwoordig. Ook in het seizoen 2019/20 werden er minder wedstrijden gespeeld, namelijk 232. Dit kwam omdat de competitie eerder stilgelegd werd vanwege COVID-19. |
|||||||||||||||||
| 3p. | 5. | Toon met behulp van de formule van W aan dat er met 232 wedstrijden geen volledige competitie gespeeld kan zijn. | |||||||||||||||
| In de tabel staan van de seizoenen 2011/12 tot en met 2021/22 de toenames (positieve getallen) of afnames (negatieve getallen) van het aantal goals per seizoen ten opzichte van het seizoen ervoor. | |||||||||||||||||
|
|||||||||||||||||
|
|||||||||||||||||
| In het seizoen
2018/19 werden er 1061 goals gescoord. Bij het seizoen 2019/20 staat: –346. Dit betekent dat er in dit seizoen 346 goals minder gescoord werden dan in 2018/19. Dit lijkt een enorme daling. In werkelijkheid valt dit wel mee, omdat er in het seizoen 2019/20 maar 232 wedstrijden gespeeld werden, ten opzichte van 306 in de andere jaren. De uitspraak “Zorgelijke trend: steeds minder goals in de Eredivisie” zegt dat er een afname is in het aantal goals, maar niet of deze afname toenemend, constant of afnemend is. Om het aantal goals in de verschillende seizoenen eerlijk met elkaar te kunnen vergelijken, berekenen we hoeveel goals er in het seizoen 2019/20 gescoord zouden zijn als er in dat seizoen niet 232 maar 306 wedstrijden gespeeld zouden zijn. We nemen daarbij aan dat in dat seizoen het aantal goals recht evenredig is met het aantal gespeelde wedstrijden. Hierdoor zullen de waardes in de tabel bij de seizoenen 2019/20 en 2020/21 veranderen. |
|||||||||||||||||
| 4p. | 6. | Onderzoek of er op basis van deze veranderde waarden sprake was van een toenemende, constante of afnemende daling van het aantal goals in de seizoenen 2020/21 tot en met 2021/22. | |||||||||||||||
| In het seizoen 2018/19 was de wedstrijd Heracles Almelo - Excelsior de wedstrijd met de meeste goals: de einduitslag was 4-5 na een ruststand van 1-2. | |||||||||||||||||
| 4p. | 7. | Bereken hoeveel verschillende scoreverlopen er mogelijk zijn voor een wedstrijd met als einduitslag 4-5 en een ruststand van 1-2. | |||||||||||||||
| Trappen. | |||||||||
|
|
|||||||||
| In
Landgraaf (Zuid-Limburg) bevindt zich de langste openluchttrap
van Nederland: de Wilhelminatrap. Zie de foto hiernaast . De 508
treden tellende trap is 248 meter lang. De treden beneden zijn
breder dan boven: beneden zijn ze 12 meter breed en boven 2
meter. Op deze manier wordt de illusie gewekt dat de trap
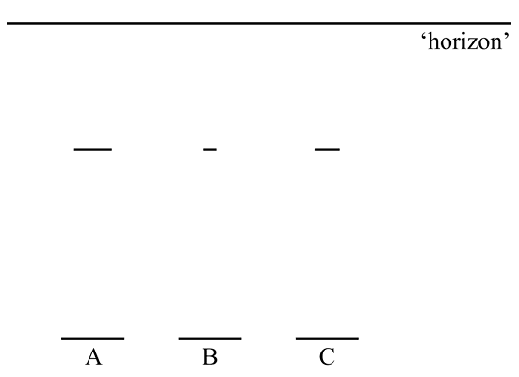
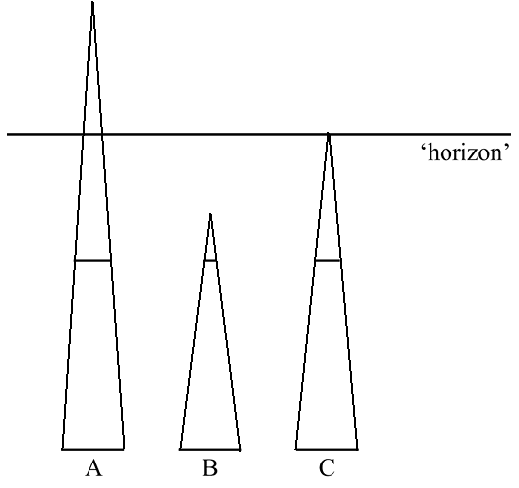
oneindig lang is. Hieronder staan drie vereenvoudigde perspectieftekeningen van de bovenste en onderste trede van een trap. Ook is de ‘horizon’ aangegeven. |
|||||||||
|
|
|||||||||
| 3p. | 8. | Beredeneer met behulp van deze figuur welke perspectieftekening (A, B of C) het beste bij de Wilhelminatrap past. | |||||||
| Er bestaan verschillende trappen en niet alle trappen lopen even gemakkelijk. Dit heeft onder andere te maken met: | |||||||||
| - | de optrede o: dit is de verticale lengte van een traptrede in cm; | ||||||||
| - | de aantrede a: dit is de horizontale lengte van een traptrede in cm; | ||||||||
| - | de helling h: de richtingscoëfficiënt van de ‘raaklijn’ aan de trap. | ||||||||
| Zie de onderstaande figuur. Er geldt: h = o/a en dan volgt: h · a = o (formule 1) | |||||||||
|
|
|||||||||
| Er zijn drie typen trappen, afhankelijk van de helling. Zie de tabel. | |||||||||
|
|||||||||
| 3p. | 9. | Bereken de mogelijke aantreden van een normale trap met een optrede van 20 cm. Geef je antwoord in gehelen. | |||||||
| De Wilhelminatrap bestaat uit 22 trapdelen, verbonden door 21 horizontale plateaus. Zie onderstaande foto en (schematisch) figuur. De trap is 248 meter lang. In de figuur rechtsonder is dit weergegeven met een stippellijn. De trap overbrugt een hoogte van 95 meter. | |||||||||
|
|
|||||||||
| Een architect wil een trap maken die net als de Wilhelminatrap 248 meter lang is en 95 meter hoog. De architect wil alle 22 trapdelen even lang en even steil maken. Ook alle plateaus worden onderling even lang. | |||||||||
| 5p. | 10. | Bereken wat de maximale lengte van één horizontaal plateau zou moeten zijn, zodat alle trapdelen nog net in de categorie luie trap vallen. Geef je antwoord in gehele cm. | |||||||
| Voor
trappen binnenshuis geldt dat deze vaak steiler zijn dan trappen
buiten (zoals bijvoorbeeld de Wilhelminatrap). Voor een trap
binnenshuis geldt meestal een helling van 0,76. Om een trap met
zo weinig mogelijk energie te betreden bedacht de Franse
architect François Blondel (al in de 17e eeuw) de volgende
formule: 2o + a = 63 (formule 2) Hierin is o de optrede in cm en a de aantrede in cm. Met behulp van formule 1 en formule 2 én een helling van 0,76 kunnen de optrede en aantrede van een zo efficiënt mogelijk te betreden trap berekend worden. |
|||||||||
| 4p. | 11. | Bereken de optrede en de aantrede van deze trap. |
|
||||||
| Niet alle
trappen lopen recht omhoog. Binnenshuis loopt een trap soms met
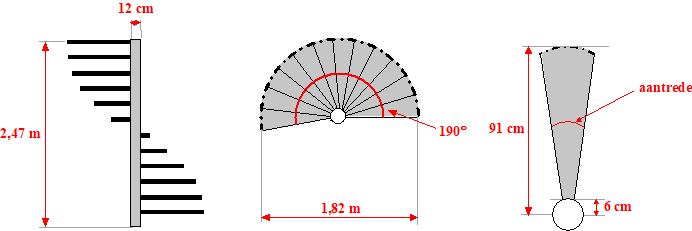
een draai, zoals de trap op onderstaande foto. In de figuur linksonder staat een vooraanzicht van deze trap, getekend vanuit de positie recht voor de paal waar de trap omheen draait. In de figuur middenonder is een bovenaanzicht van deze trap te zien, waarin de treden elkaar niet overlappen. In de figuur rechtsonder is een losse trede van de trap te zien. |
|||||||||
|
|
|||||||||
| Verder geldt: | |||||||||
| - | De trap is 2,47 meter hoog. | ||||||||
| - | De trap maakt een draai van 190 graden. | ||||||||
| - | De buitendiameter van de trap is 1,82 meter en de binnendiameter is 12 cm. | ||||||||
| - | De 12 treden van de trap hebben allemaal precies dezelfde vorm en afmetingen. | ||||||||
| - | De 12 optreden van deze trap zijn allemaal even groot. | ||||||||
| We nemen voor de aantrede de lengte van de cirkelboog die precies door het midden van een trede loopt. Zie de figuur rechts. Met behulp van de formule van de omtrek van een cirkel (omtrek cirkel 2π · straal) is deze aantrede te berekenen. | |||||||||
| 5p. | 12. | Bereken of hier sprake is van een steile, normale of luie trap. | |||||||
| Dr. Nim | ||||
| The
Amazing Dr. Nim is een bordspel uit de jaren 60 van de
vorige eeuw. Het is een spel voor één speler, waarbij het
spel zelf (Dr. Nim) de tegenstander is. Het spel werkt met een ingenieus systeem van schakelaartjes die ervoor zorgen dat Dr. Nim een bepaalde strategie kan uitvoeren. De spelregels zijn eenvoudig: het spel begint met 12 knikkers. De speler is altijd eerst aan de beurt en mag in zijn beurt 1, 2 of 3 knikkers pakken. Daarna mag Dr. Nim op zijn beurt 1, 2 of 3 knikkers pakken. Dit gaat zo door tot er geen knikkers meer over zijn. Degene die de laatste knikker pakt wint. Als je het spel met slechts 4 knikkers zou spelen in plaats van 12, kan Dr. Nim altijd winnen. |
 |
|||
| 2p. | 13. | Licht dat toe. | ||
| Voor het vervolg van de opgave voeren we de volgende notaties in: | ||||
| - | Sn betekent: "de speler pakt n knikkers" | |||
| - | Dn betekent ‘Dr. Nim pakt n knikkers’ | |||
| - | W betekent ‘de speler kan winnen’ | |||
| Bij dit spel met 12 knikkers is de strategie van Dr. Nim als volgt: | ||||
|
||||
| 4p. | 14. | Vertaal elk van de drie stappen van deze strategie, gebruikmakend van de bovenstaande notaties, in logische symbolen en leg uit waarom deze strategie altijd tot winst voor Dr. Nim zal leiden. | ||
| Het
spel is niet zo leuk als je altijd verliest, dus daarom is
het ook mogelijk om Dr. Nim een foutje te laten maken. Een
speler kan het spel zó instellen dat Dr. Nim niet volgens de
eerder genoemde strategie speelt, waardoor de speler een
kans heeft om te winnen. Bij deze nieuwe spel-instelling zal Dr. Nim alleen in zijn eerste beurt een foutje maken. Dat geeft de speler één kans om het spel te winnen door in zijn tweede beurt precies het juiste aantal knikkers te pakken. Als de speler het verkeerde aantal knikkers pakt, zal Dr. Nim een slimme tegenzet doen en daardoor het spel winnen. We voeren de volgende extra notaties in: |
||||
| - | En betekent ‘de speler pakt in de eerste beurt n knikkers’ | |||
| - | Tn betekent ‘de speler pakt in de tweede beurt n knikkers’ | |||
| Hieronder staan twee logische beweringen die gaan over de variant waarin Dr. Nim in zijn eerste beurt een foutje maakt. | ||||
| 1. | (E2 ∧ D3 ∧ ¬ T3) ⇒ ¬ W | |||
| 2. | (E2 ∧ (D2 ∨ D3) ⇒ W | |||
| 4p. | 15. | Vertaal deze beweringen in een gewone Nederlandse zin en leg van elke bewering uit of deze juist is. | ||
| Procenten en zwemtijden. | |||
| Bij
wedstrijdzwemmen kunnen verschillende afstanden en
slagen gezwommen worden. Er kan bijvoorbeeld de 25 meter
vlinderslag, de 50 meter rugslag of de 100 meter
schoolslag gezwommen worden. Op de website
www.swimrankings.net wordt van veel zwemwedstrijden de
uitslag gepubliceerd. Op deze website worden ook ranglijsten en persoonlijke records van zwemmers bijgehouden. Een persoonlijk record is de snelste tijd die een persoon ooit gezwommen heeft op een bepaalde afstand en met een bepaalde slag. In de uitslagen van wedstrijden worden onder andere de gezwommen tijd, het oude persoonlijke record en een percentage genoemd. Dit percentage geeft aan hoe goed de gezwommen tijd is ten opzichte van het oude persoonlijke record. Het percentage wordt op een heel andere manier berekend dan de standaardberekening met procentuele toenames. Daarom noemen we dat percentage in deze opgave de Swimrankingsscore en niet een percentage. De Swimrankingsscore wordt berekend met de formule: |
|||
|
|
|||
| Hierin is Ssw de Swimrankingsscore, o het oude persoonlijke record in seconden en n de gezwommen tijd in seconden. Als een zwemmer een persoonlijk record verbetert, dan is meestal de Swimrankingsscore tussen de 100 en 120. Er zijn echter uitzonderingen, zo zwom Myrthe in november 2022 op de 25 meter vlinderslag een Swimrankingsscore van 287,7. Haar oude persoonlijke record was 29,77 seconden. | |||
| 3p. | 16. | Bereken de tijd die Myrthe in november 2022 zwom. Geef je antwoord in seconden in twee decimalen. | |
| In
formule 1 worden o en n als losse
variabelen gebruikt, maar vooral de verhouding r
= n/o is van belang. Er geldt: |
|||
| - | Als 0 < r < 1, dan is er sprake van een verbetering van het persoonlijk record. | ||
| - | Als r ³ 1, dan is er geen verbetering van het persoonlijk record. | ||
| Formule 1 kan worden herschreven tot: | |||
|
|
|||
| Er
kan ook een alternatieve Swimrankingsscore worden
bepaald. Daarbij hoort de volgende formule: Salt = 200 - 100r (formule 3) |
|||
| Hierin is Salt de alternatieve Swimrankingsscore en r = n/o (met o het oude persoonlijke record in seconden en n de gezwommen tijd in seconden). | |||
| 3p. | 17. | Onderzoek of het mogelijk is dat formule 2 en formule 3 dezelfde uitkomst geven, als een zwemmer zijn persoonlijk record niet verbeterd heeft. | |
| Gegeven zijn de volgende twee beweringen: | |||
| 1. | De uitkomsten van Ssw en Salt zijn altijd positief. | ||
| 2. | Als er gerekend wordt met Salt in plaats van Ssw dan kun je nooit een Swimrankingsscore van 287,7 halen. | ||
| 4p. | 18. | Geef van beide beweringen aan of ze wel of niet waar zijn. Licht je antwoord toe. | |
| CO2 in de atmosfeer | |||
| In deze opgave kijken we naar het verloop van de concentratie CO2 in de atmosfeer. Onderzoekers hebben geconstateerd dat de natuurlijke concentratie CO2 eeuwenlang stabiel is gebleven rond de 280 ppm (parts per million). De toename van de concentratie CO2 sinds de industriële revolutie wordt met name veroorzaakt door massaproductie van goederen en voedsel. In de figuur zie je het verloop van de concentratie CO2 in de periode 1800–2009. | |||
|
|
|||
| De toename verloopt
exponentieel. Het verloop van de concentratie CO2 kan worden
benaderd met het model: C = 280 + gt Hierbij is C de concentratie CO2 in ppm en t de tijd in jaren met t = 0 op 1 januari 1800. De waarde 280 staat in dit model voor de constante natuurlijke concentratie CO2. Op 1 januari 2002 was de concentratie CO2 370 ppm. Met dit gegeven en met behulp van bovenstaande gegevens is te berekenen dat de waarde van g, afgerond op vier decimalen, gelijk is aan 1,0225. |
|||
| 3p. | 19. | Bereken de waarde van g in vijf decimalen. | |
| 3p. | 20. | Bereken in welk jaar de concentratie CO2 verdubbeld zal zijn ten opzichte van de natuurlijke concentratie. | |
| Zoals je in de
figuur kunt zien is de grafiek toenemend stijgend. De formule C =
280 · 1,0225t
benadert deze stijging. Vanaf 1800 duurde het 150 jaar totdat de concentratie CO2 met (ongeveer) 10% was toegenomen. Vanaf 1950 duurde het veel korter totdat de volgende 10% stijging van de concentratie CO2 werd gemeten. |
|||
| 4p. | 21. | Bereken hoeveel gehele jaren hiervoor nodig waren. | |