| Groeipercentages wereldbevolking. | |||
| De wereldbevolking
is gedefinieerd als het totaal aantal levende mensen op aarde op een
bepaald moment. Het blijkt moeilijk te zijn om op een bepaald moment de
wereldbevolking exact te bepalen, daarom wordt de wereldbevolking in
werkelijkheid altijd geschat. Hierbij worden verschillende modellen
gebruikt. Begin 2019 werd op basis van een van die modellen de
wereldbevolking op 7,67 miljard mensen geschat. Volgens hetzelfde model zou dat 7,1% zijn van het totaal aantal mensen dat tot dan toe ooit op aarde had geleefd. |
|||
| 2p. | 1. | Bereken hoeveel mensen er volgens dit model tot 2019 ooit op aarde hebben geleefd. Geef je antwoord in gehele miljarden. | |
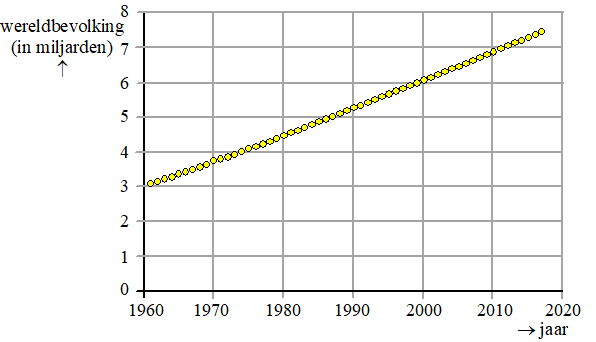
| De wetenschapper Doug Boucher beweerde in 2018 dat de wereldbevolking al ruim een halve eeuw bij benadering lineair groeide. Hij baseerde dit lineaire model op historische gegevens. Zie onderstaande figuur. | |||
|
|
|||
| Voor zijn lineaire
benadering gebruikte Boucher dat de wereldbevolking groeide van 3,084
miljard halverwege 1961 tot 7,330 miljard halverwege 2016. Veronderstel dat Bouchers lineaire benadering ook na 2016 bleef gelden, dan volgt hieruit een lagere schatting voor de wereldbevolking begin 2019 dan de eerder genoemde schatting van 7,67 miljard. |
|||
| 3p. | 2. | Bereken hoeveel lager de schatting volgens Bouchers lineaire benadering uitvalt. Geef je antwoord in gehele miljoenen. | |
| Als de wereldbevolking bij benadering lineair groeit, dan zal het jaarlijkse groeipercentage afnemen. | |||
| 2p. | 3. | Beredeneer dit zonder gebruik te maken van een getallenvoorbeeld. | |
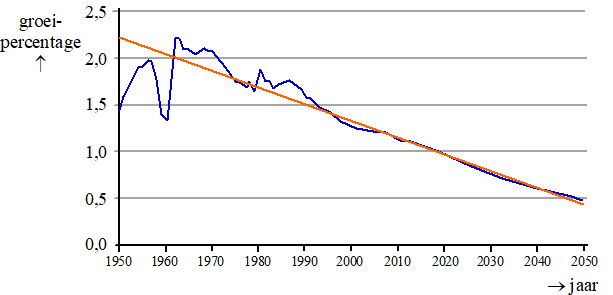
| In de volgende figuur zijn de jaarlijkse groeipercentages voor de periode 1950-2050 weergegeven. Hierbij zijn de percentages na 2013 voorspelde percentages. Bovendien is een trendlijn getekend. | |||
|
|
|||
| In tegenstelling
tot het model van Boucher waarin de wereldbevolking lineair zou
toenemen, geeft de trend in figuur 2 aanleiding voor een ander model
waarin de groeipercentages lineair afnemen. Een formule voor de trendlijn in deze figuur is: P = -0,0177t + 2,2153 |
|||
| Hierin is P
het jaarlijkse groeipercentage en t de tijd in jaren met t
= 0 het jaar 1950. In de formule van de trendlijn kun je zien dat in 1950 de wereldbevolking toenam met afgerond 2,2%. Er zijn wetenschappers die vermoeden dat aan het eind van deze eeuw de wereldbevolking nauwelijks nog zal groeien of op termijn misschien zelfs gaat afnemen. Stel dat de groeipercentages zich ook na 2050 volgens de formule van P zullen blijven ontwikkelen. |
|||
| 3p. | 4. | Bereken in welk jaar de wereldbevolking dan voor het eerst zal afnemen. | |
| Turm. | |||
| De Duitse tekenaar en beeldhouwer Erwin Heerich (1922–2004) maakte in zijn werk vaak gebruik van eenvoudige ruimtelijke figuren. Later in zijn carrière ontwierp hij ook gebouwen. | |||
 |
|||
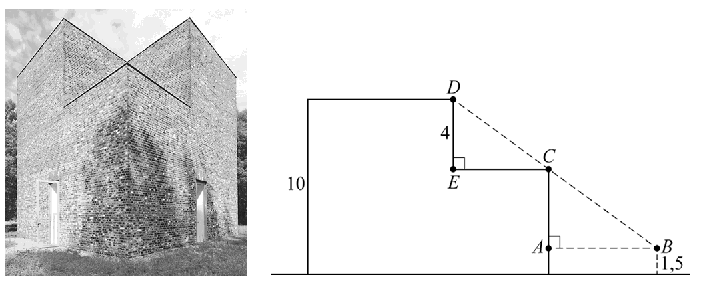
| Op de foto
hiernaast zie je zijn Turm (Duits voor 'toren'), die
hij bedacht voor het openluchtmuseum Museum Insel Hombroich bij
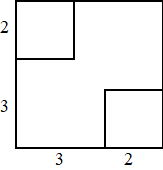
Neuss in Duitsland. Turm heeft de vorm van een kubus met een ribbe van 10 meter. Op een hoogte van 6 meter zijn diagonaal tegenover elkaar twee kubussen met een ribbe van 4 meter weggelaten. |
|||
| 2p. | 5. | Teken op schaal 1 : 200 het bovenaanzicht van Turm. | |
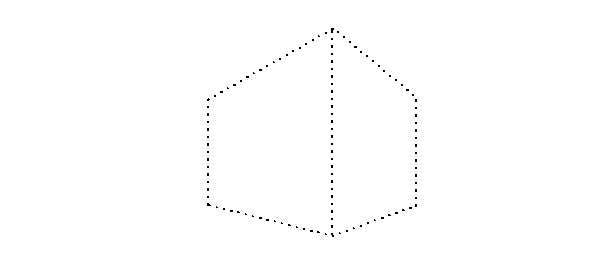
| Hieronder staat een gestippelde perspectieftekening van een kubus. | |||
|
|
|||
| 6p. | 6. | Teken in de figuur op de uitwerkbijlage de perspectieftekening van Turm, zonder deuren, vanuit het aanzicht van de foto. | |
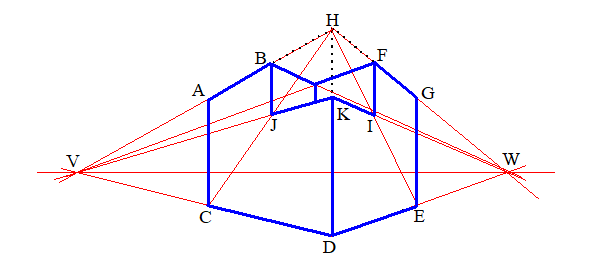
| Op de volgende foto is Turm vanuit een bijzonder perspectief gefotografeerd waarbij twee hoekpunten van een van de weggelaten kubussen samenvallen. | |||
|
|
|||
| Deze foto is op anderhalve meter hoogte genomen, waarbij de camera van de fotograaf precies op het (denkbeeldige) verlengde van een diagonaal van het grondvlak van Turm stond. In de figuur is schematisch de positie van de fotocamera, in punt B, ten opzichte van Turm weergegeven. Uit de gegevens volgt dat EC een diagonaal van een vierkant met zijden van 4 meter is. | |||
| 3p. | 7. | Bereken, zonder te meten, op welke afstand vanaf Turm deze foto gemaakt is. Geef je antwoord in meters in één decimaal. | |
| Maakt geld gelukkig? | ||||
| Een veelgehoorde
bewering is dat geld niet gelukkig maakt. Een groep onderzoekers
heeft deze bewering in het begin van deze eeuw onderzocht.
Hiervoor hebben respondenten uit 132 landen een identieke
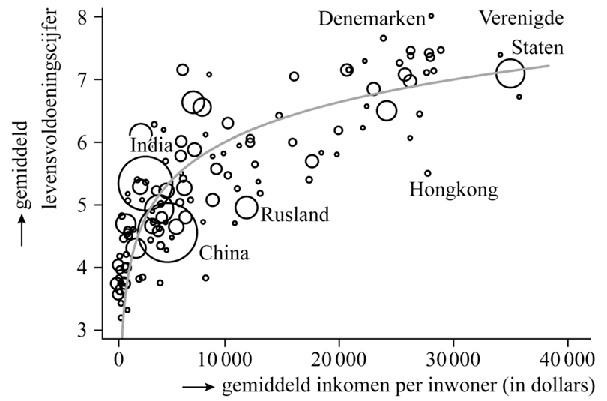
vragenlijst ingevuld. Bij een van de vragen uit deze vragenlijst moesten de respondenten hun leven een cijfer geven op een schaal van 0 tot 10. Dit werd het levensvoldoeningscijfer genoemd. In de figuur is van de 132 landen uit het onderzoek, die zijn weergegeven als cirkels, het gemiddelde levensvoldoeningscijfer uitgezet tegen het gemiddelde inkomen per inwoner in dollars van dat land. |
||||
|
|
||||
| In de figuur is ook een
trendlijn getekend. Deze trendlijn volgt zo goed mogelijk de
landencirkels. Een formule van deze trendlijn is: 2 L = 0,6 · 2log(I) - 1,973 Hierin is L het gemiddelde levensvoldoeningscijfer (met voor L een waarde vanaf 0 tot en met 10) en I het gemiddelde inkomen per inwoner in dollars. Omdat de levensvoldoening alleen maar met een cijfer vanaf 0 tot en met 10 beoordeeld kan worden, is de formule van de trendlijn enkel tussen bepaalde inkomensgrenzen geldig. |
||||
| 3p. | 8. | Bereken deze grenzen. Geef je antwoord in gehele dollars. | ||
| In de figuur is te zien dat over het algemeen geldt dat hoe hoger het gemiddelde inkomen is, hoe hoger de levensvoldoening is. Dit is niet overal het geval. Zo geldt voor Denemarken en Hongkong dat het gemiddelde inkomen per inwoner bijna even hoog is, namelijk 28000 dollar. De levensvoldoening is in Denemarken echter aanzienlijk hoger dan in Hongkong. Bij beide landen wijkt het levensvoldoeningscijfer behoorlijk af van wat je op basis van de formule van de trendlijn zou verwachten. | ||||
| 3p. | 9. | Onderzoek met behulp van de figuur en de formule van de trendlijn bij welk van deze twee landen de afwijking het grootst is. | ||
| Op basis van de onderzoeksresultaten deden de onderzoekers de volgende uitspraak: | ||||
|
||||
| 3p. | 10. | Bereken met behulp van de formule L = 0,6 · 2log(I) - 1,973 hoe groot de toename is bij een verdubbeling van I. Geef je antwoord in één decimaal. | ||
| Lootjes trekken. | |||||||||||||||||
| Veel groepen en families trekken voor Sinterklaas of Kerstmis lootjes om te bepalen wie aan wie een cadeautje geeft. Het trekken van lootjes kan met behulp van papiertjes worden gedaan. Daarover gaat deze opgave. Dit lootjes trekken gaat als volgt: | |||||||||||||||||
| - | Elke deelnemer schrijft de eigen naam op een papiertje. | ||||||||||||||||
| - | Vervolgens worden deze zogenaamde lootjes in een zak gestopt. | ||||||||||||||||
| - | Daarna trekt iedereen willekeurig blind één lootje uit de zak. | ||||||||||||||||
| Als
iemand het eigen lootje trekt, moeten alle lootjes weer
worden ingeleverd en worden de lootjes opnieuw getrokken.
We noemen het trekken van lootjes anoniem als iedereen alleen de naam weet op het lootje dat hij/zij getrokken heeft en van geen enkel ander lootje kan beredeneren door wie het getrokken is. De verdeling van de lootjes over de verschillende personen noemen we goed als niemand het eigen lootje heeft en als het lootjes trekken anoniem is. We voeren de volgende notaties in: |
|||||||||||||||||
| Z | Minstens één persoon heeft het eigen lootje getrokken. | ||||||||||||||||
| A | Het lootjes trekken is anoniem. | ||||||||||||||||
| G | De verdeling van de lootjes is een goede verdeling. | ||||||||||||||||
| Gegeven
is de zin: Als niemand het eigen lootje getrokken heeft en het lootjes trekken is anoniem, dan is de verdeling van de lootjes een goede verdeling. |
|||||||||||||||||
| 2p. | 11. | Vertaal de gegeven zin in logische symbolen, gebruikmakend van bovenstaande notatie. | |||||||||||||||
| Als de
verdeling van de lootjes niet goed is, dan heeft minstens
één persoon het eigen lootje getrokken en/of is het lootjes
trekken niet anoniem. Met twee personen is er geen goede verdeling van lootjes mogelijk. Immers: |
|||||||||||||||||
| - | Als je je eigen lootje trekt, dan is de verdeling niet goed. Bovendien weet je dan ook dat de ander zichzelf heeft en is het daarmee ook niet anoniem. | ||||||||||||||||
| - | Als je het lootje van de ander trekt, dan weet je dat de ander jouw lootje heeft getrokken en is het lootjes trekken niet anoniem. | ||||||||||||||||
| Ook
voor drie personen is het niet mogelijk om een goede
verdeling te krijgen. Sem, Finn en Rik gaan lootjes trekken. |
|||||||||||||||||
| 4p. | 12. | Beredeneer dat er bij deze drie personen geen goede verdeling van de lootjes mogelijk is. | |||||||||||||||
| Een groep van zes personen gaat lootjes trekken. Bij zes personen is lootjes trekken altijd anoniem, zolang mensen niet vertellen welk lootje zij getrokken hebben. In het vervolg van deze opgave hoef je dus geen rekening meer te houden met de anonimiteit. Een mogelijke verdeling van de lootjes is in de tabel weergegeven. | |||||||||||||||||
|
|||||||||||||||||
| Zonder het van elkaar te weten, vormen P, Q en R een subgroep binnen de groep van zes personen. De drie personen trekken in een soort kringetje elkaars lootje. Dit noemen we een kringetje van lengte 3. Ook S, T en U vormen een kringetje van lengte 3. Omdat niemand het eigen lootje heeft, is er sprake van een goede verdeling. Met de notatie Kn wordt bedoeld dat er ten minste één kringetje van lengte n aanwezig is in de verdeling van de lootjes. De volgende twee beweringen worden gedaan over het lootjes trekken met zes personen: | |||||||||||||||||
| - | K5 ⇒ G | ||||||||||||||||
| - | (K4 ∧ G) ⇒ K2 | ||||||||||||||||
| 4p. | 13. | Vertaal elk van de twee beweringen naar een zin en geef van elke zin aan of de bewering waar is of niet. Licht je antwoord toe. | |||||||||||||||
| Pokémon GO | |||
|
Pokémon GO is een spel dat je via een app op een
smartphone kunt spelen. Het spel werd op 6 juli 2016
uitgebracht door Nintendo en werd al snel een van de
populairste spellen op een smartphone. In de eerste twee weken na de lancering van Pokémon GO nam het aantal gebruikers spectaculair toe tot 45 miljoen wereldwijd. |
|||
| 2p. | 14. | Bereken hoeveel gebruikers er gemiddeld per minuut bij kwamen in deze periode. Geef je antwoord in tientallen nauwkeurig. | |
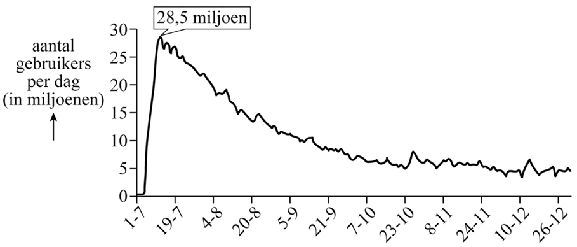
| Pokémon GO was na de lancering veruit het populairst in de Verenigde Staten (VS). De volgende vragen gaan over het aantal gebruikers per dag van Pokémon GO in de Verenigde Staten. In de volgende figuur is dit aantal voor de periode juli 2016 tot en met december 2016 weergegeven. | |||
|
|
|||
| In de eerste week na de lancering van het spel op 6 juli 2016 nam het aantal gebruikers per dag toe tot maximaal 28,5 miljoen op 13 juli 2016. Na 13 juli 2016 nam het aantal gebruikers per dag alweer af. De afname verliep in het begin bij benadering lineair tot 15,1 miljoen gebruikers op 12 augustus 2016. | |||
| 3p. | 15. | Bereken met behulp van deze gegevens het aantal gebruikers per dag in de VS op 1 augustus 2016. Geef je antwoord in gehele miljoenen. | |
| Een
formule waarmee het aantal gebruikers per dag vanaf 12
augustus 2016 benaderd kan worden, is: N = 10,5 · 0,972t + 4,6 Hierin is N het aantal gebruikers per dag in de VS in miljoenen en t de tijd in dagen met t = 0 op 12 augustus 2016. |
|||
| 4p. | 16. | Bereken hoeveel gehele dagen na de lancering van Pokémon GO op 6 juli het aantal gebruikers per dag in de VS voor het eerst minder dan een kwart was van het maximale aantal gebruikers per dag in de VS. | |
|
Pokémon GO bestaat uit 40 levels. Een van de redenen dat
flink wat gebruikers van Pokémon GO weer afhaken, is dat
het steeds moeilijker wordt om een volgend level in het
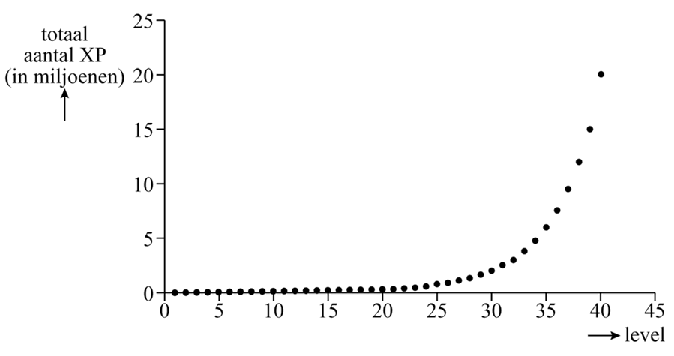
spel te bereiken. Om een volgend level te bereiken, moet je een bepaald totaal aantal punten behaald hebben. Dit worden XP (Experience Points) genoemd. Zie onderstaande figuur. |
|||
|
|
|||
|
Vanaf level 22 blijkt er bij benadering een exponentieel
verband te bestaan tussen het level en het totaal aantal
behaalde XP. Bij level 22 horen 335000 XP en bij level
40 wel 20000000 XP. Uit de gegevens volgt dat afgerond op drie decimalen de groeifactor van het totaal aantal behaalde XP per level gelijk is aan 1,255. |
|||
| 3p. | 17. | Bereken met behulp van de gegevens deze groeifactor in vier decimalen. | |
| Youtuber Brandon Tan bereikte op een gegeven moment level 40. Naar eigen zeggen behaalde hij tussen level 39 en level 40 gemiddeld 300 000 XP per dag. | |||
| 3p. | 18. | Bereken hoeveel dagen hij volgens de gegevens bezig is geweest om van level 39 naar level 40 te komen. Maak gebruik van de groeifactor en geef je antwoord in gehele dagen. | |
| De slimste mens. | |||
| ‘De slimste
mens’ is een televisiequiz. In elke aflevering van deze quiz
strijden drie kandidaten tegen elkaar. In verschillende rondes
moet geprobeerd worden zoveel mogelijk seconden te verdienen
door juiste antwoorden te geven. De kandidaat die aan het einde
de meeste seconden heeft, is 'De slimste van de dag'. Van deze quiz worden per jaar twee seizoenen uitgezonden, één in de zomer en één in de winter. Elk seizoen bevat 30 of 35 afleveringen. Alleen het 11e seizoen bevatte slechts 5 afleveringen. In de zomer van 2020 werd het 17e seizoen uitgezonden. De 30e aflevering van dit seizoen was de 500e aflevering van deze quiz. |
|||
| 3p. | 19. | Bereken hoeveel van de seizoenen vóór dit 17e seizoen uit 35 afleveringen bestonden. | |
| Bij de eerste ronde van de quiz start iedere kandidaat met 60 seconden. In deze ronde kunnen vijf keer 10 seconden worden verdiend. Een mogelijke stand na de eerste ronde is: kandidaat A heeft 70 seconden, kandidaat B heeft 80 seconden en kandidaat C heeft 70 seconden. In totaal zijn er dan 40 seconden verdiend in deze ronde. | |||
| 4p. | 20. | Bereken hoeveel verschillende standen er na de eerste ronde mogelijk zijn als er in deze ronde in totaal 40 seconden worden verdiend. | |
| Bij de laatste ronde worden drie filmfragmenten getoond. Bij ieder fragment moeten vijf trefwoorden worden genoemd. Hierbij gelden de volgende regels: | |||
| - | Per fragment levert het trefwoord dat als eerste juist genoemd wordt 10 seconden op, het tweede 20 seconden en zo verder tot 50 seconden voor het vijfde juist genoemde trefwoord. Dit is onafhankelijk van welke kandidaat het juiste antwoord geeft. | ||
| - | Als bij een fragment de eerste kandidaat niet alle juiste trefwoorden heeft gegeven, mogen de andere twee kandidaten proberen de overige juiste trefwoorden te noemen. De kandidaat die op dat moment de minste seconden heeft, mag dit als eerste proberen. | ||
| - | Het aantal seconden dat een kandidaat nodig heeft om na te denken en trefwoorden te noemen wordt in mindering gebracht. | ||
| De kandidaat die aan het einde van deze ronde de meeste seconden heeft, is 'De slimste van de dag'. Bij een aflevering was de stand voor aanvang van de laatste ronde: | |||
| - | kandidaat A: 254 seconden | ||
| - | kandidaat B: 273 seconden | ||
| - | kandidaat C: 222 seconden | ||
| Kandidaat C
mocht bij de laatste ronde beginnen en wist vier juiste
trefwoorden te geven in 13 seconden. Vervolgens gaf kandidaat A
geen juist trefwoord, maar gebruikte wel 6 seconden om na te
denken. Kandidaat B paste direct en verspeelde daardoor geen
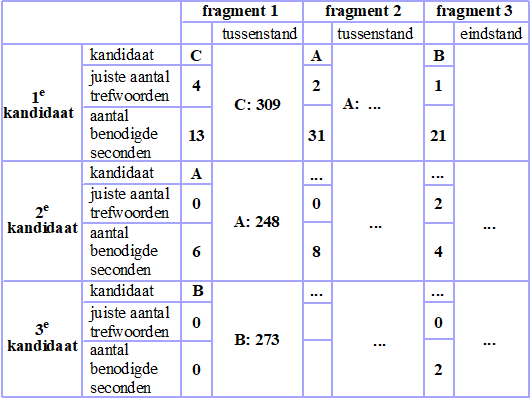
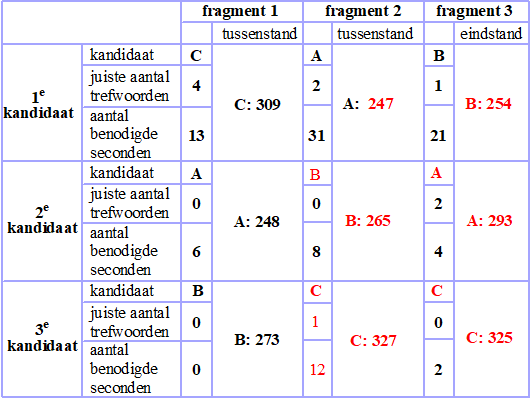
seconden. In de tabel op de uitwerkbijlage is de tussenstand van de kandidaten na fragment 1 al ingevuld. Verder is voor de overige fragmenten weergegeven hoeveel trefwoorden een kandidaat goed had en hoeveel seconden de kandidaat daarvoor nodig had. Ook is te zien dat kandidaat A bij fragment 2 mocht beginnen en kandidaat B bij fragment 3. |
|||
|
|
|||
| 5p. | 21. | Bereken welke kandidaat deze aflevering 'De slimste van de dag' was. Je kunt hierbij gebruikmaken van de tabel. | |
| Zonnebloemen. | |||
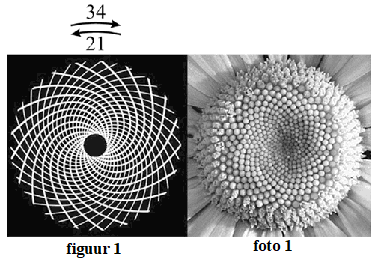
| Als je goed
naar een zonnebloem kijkt, dan kun je zien dat de
pitten geordend zijn in spiralen. Er zijn spiralen
die linksom draaien en spiralen die rechtsom
draaien. In figuur 1 en foto 1 zie je bijvoorbeeld een zonnebloem met 21 linksom draaiende en 34 rechtsom draaiende spiralen. De getallen 21 en 34 zijn opvallend, omdat het twee opeenvolgende getallen uit de rij van Fibonacci zijn. |
|||
|
|
|||
| In deze
opgave bedoelen we met een spiralenpaar het aantal
linksom draaiende en het aantal rechtsom draaiende
spiralen in een specifieke zonnebloem. We noteren
deze spiralenparen steeds tussen haakjes met het
kleinste aantal eerst. Het spiralenpaar uit foto 1
wordt dus genoteerd als (21 , 34). Met een
fibonacci-spiralenpaar bedoelen we dat het
spiralenpaar uit twee opeenvolgende getallen uit de
rij van Fibonacci bestaat. Het spiralenpaar uit foto
1 is dus een fibonacci-spiralenpaar. Een recursieve formule van de rij van Fibonacci is: Fn = Fn - 1 + Fn - 2 met F0 = F1 = 1 Hieronder staan nog vijf andere foto's van zonnebloemen uit het onderzoek, met de bijbehorende spiralenparen. |
|||
|
|
|||
| 2p. | 22. | Onderzoek op welke van deze foto's zonnebloemen staan afgebeeld met een fibonacci-spiralenpaar. | |
|
In 2012 werd er door het Manchester Museum of
Science and Industry een onderzoek gestart naar de
aanwezigheid van fibonacci-spiralenparen in
zonnebloemen. Voor het onderzoek waren veel
zonnebloemen nodig en daarom konden geïnteresseerde
mensen zelf zonnebloemen kweken, het aantal spiralen
tellen en de gegevens insturen. De onderzoekers leverden gegevens van 768 zonnebloemen aan en het publiek van 1281 zonnebloemen. Hiervan bleek afgerond respectievelijk 74% en 64% van de zonnebloemen een fibonacci-spiralenpaar te hebben. |
|||
| 3p. | 23. | Bereken hoeveel procent van het totaal aantal onderzochte zonnebloemen een fibonacci-spiralenpaar had. Geef je antwoord in gehelen. | |
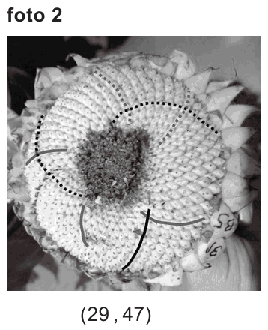
|
Niet alle zonnebloemen blijken dus
fibonacci-spiralenparen te hebben. Toch is er bij de
andere spiralenparen vaak wel iets bijzonders aan de
hand, waardoor de andere zonnebloemen ook kunnen
worden ingedeeld in zogeheten families. De zonnebloem van foto 2 heeft het spiralenpaar (29 , 47) en behoort tot een andere familie dan de zonnebloemen met fibonacci-spiralenparen. Bij de familie van deze bloem zijn de spiralenparen twee opeenvolgende getallen uit een andere rij. Deze rij is wel vergelijkbaar met de rij van Fibonacci, want ook voor deze rij geldt dat elke term de som is van de twee voorafgaande termen. |
|||
|
|
|||
| Van de familie van zonnebloemen uit foto 2 is het kleinste aantal spiralen 11 en het grootste aantal spiralen 123. | |||
| 3p. | 24. | Geef alle mogelijke spiralenparen uit deze familie. Licht je antwoord toe. | |