| Balonnen. | |||
| Bij feestwinkel De
Zevenklapper zijn heliumballonnen te koop. De ballonnen worden in de
winkel door een speciale machine gevuld met een mengsel van helium en
lucht, beter bekend als ballongas. Ballongas wordt verkocht in cilinders die op een vulmachine kunnen worden aangesloten. Het voordeel van een vulmachine is dat het opblazen van de ballonnen heel snel gaat, maar het nadeel is dat er bij het vullen nog weleens wat ballongas verloren gaat. Een medewerker van De Zevenklapper weet uit ervaring dat de vulmachine met een cilinder, gevuld met 0,5 m3 ballongas, precies 52 ballonnen kan vullen met 9 dm3 ballongas. |
|||
| 3p. | 1. | Bereken hoeveel procent van het ballongas verloren gaat tijdens het vullen van deze 52 ballonnen met de vulmachine. Geef je antwoord in één decimaal. | |
| Als er te veel ballongas in een ballon geblazen wordt, zal deze op een bepaald moment knappen. Dat komt doordat de latex waarvan de ballon is gemaakt dan zo veel uitgerekt is, dat deze kapotgaat. | |||
| Het is lastig om
precies op het foto goede moment een foto te maken waarop een ballon
knapt, zoals de foto hiernaast. Hiervoor maakt men een filmpje van het
opblazen en knappen van de ballon. Dan wordt het filmbeeld gezocht
waarop het knappen te zien is. Met een goede camera kunnen 250, 420 of
1000 beelden per seconde worden gemaakt. Stel dat het knappen van een ballon 3 milliseconden duurt. |
|
||
| 4p. | 2. | Onderzoek bij de drie bovengenoemde filmbeeldsnelheden of het knappen van de ballon altijd op een filmbeeld te zien is. | |
| Latex is niet
helemaal luchtdicht, waardoor ballonnen langzaam leeglopen. Hoe snel dat
gaat, hangt af van veel factoren. In het vervolg van deze opgave gaan we
ervan uit dat voor de hoeveelheid ballongas H in dm3
van een ballon die werd gevuld met 9 dm3 ballongas geldt: H(t) = 9 0,98t , met t de tijd in uren nadat de ballon is opgeblazen. |
|||
| 2p. | 3. | Bereken met hoeveel procent de hoeveelheid ballongas per dag afneemt. Geef je antwoord in hele procenten. | |
| Een ballon zal niet meer zweven als 30% van het ballongas uit de ballon verdwenen is. De Zevenklapper biedt de mogelijkheid om de ballonnen te bewerken met een zogenoemde hi-floatcoating, waardoor de ballonnen langer blijven zweven. De ballonnen worden dan voorzien van een speciale laag gel, waardoor er per uur nog maar 1% lucht uit wegloopt. | |||
| 4p. | 4. | Onderzoek hoeveel uur een ballon met de hi-floatcoating langer zweeft dan een ballon die niet met de hi-floatcoating bewerkt is. Geef je antwoord in hele uren. | |
| Supermaan. | ||||||||||||||||||||||||||||||||||||||||||
| De maan beweegt in
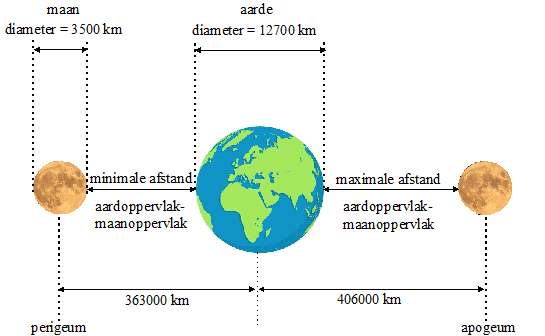
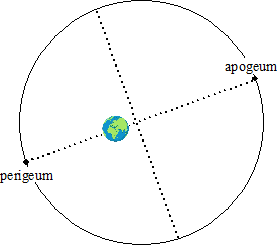
een baan om de aarde. Deze baan is niet volmaakt cirkelvormig. Hierdoor staat de maan niet altijd even dicht bij de aarde. Het punt waar de maan het dichtst bij de aarde staat heet perigeum en het punt waar deze afstand het grootst is heet apogeum. Zie de figuur hiernaast. |
 |
|||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
| 2p. | 5. | Bereken met behulp van de afmetingen in bovenstaande figuur de minimale afstand en de maximale afstand in km van het aardoppervlak tot het maanoppervlak. | ||||||||||||||||||||||||||||||||||||||||
| Afhankelijk van de
positie van de maan ten opzichte van de aarde en de zon zien we een
groter of kleiner deel van de verlichte kant van de maan. Gemiddeld één
keer per 29,53 dagen is de verlichte maan helemaal zichtbaar. We noemen
dat volle maan. Er is een supermaan als het volle maan is op dezelfde dag dat de maan in het perigeum staat. Doordat de maan in gemiddeld 27,55 dagen om de aarde draait, komt dit niet vaak voor. Je kunt berekenen hoeveel dagen er steeds tussen twee supermanen zitten door de periode van zowel de volle maan als van het perigeum te bekijken. In de tabel is daar een begin mee gemaakt. In de tweede en derde kolom zie je het aantal dagen na een supermaan. |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
| De eerste drie
volle manen vallen op de 30e, 59e en 89e dag, terwijl de maan op de 28e,
55e en 83e dag in het perigeum staat. Gedurende de eerste 89 dagen na
een supermaan vallen de twee verschijnselen dus nooit op dezelfde dag en
is er dus ook geen supermaan. Door de tabel uit te breiden en verder in te vullen kun je onderzoeken hoeveel dagen het duurt voordat er weer een supermaan is. |
||||||||||||||||||||||||||||||||||||||||||
| 4p. | 6. | Voer dit onderzoek uit. | ||||||||||||||||||||||||||||||||||||||||
| In de praktijk wordt er een ruimere definitie voor een supermaan gebruikt: | ||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
| Deze ruimere
definitie van een supermaan leidt ertoe dat er soms meerdere supermanen
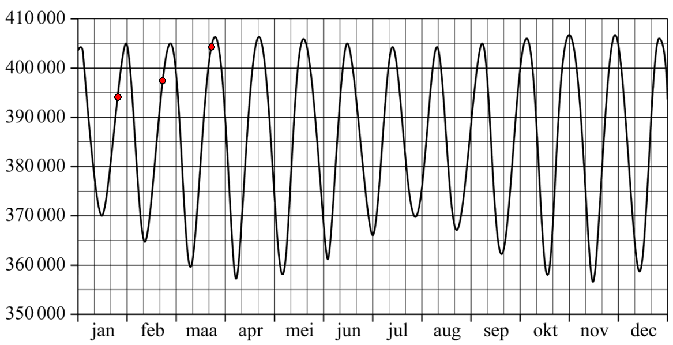
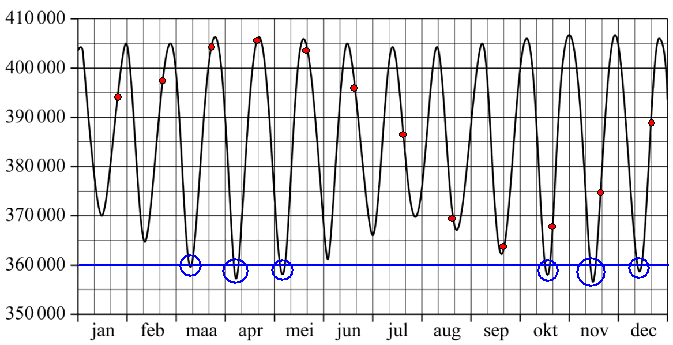
in een jaar kunnen voorkomen. In 2016 waren er zelfs drie! De minimale afstand van het middelpunt van de aarde tot het middelpunt van de maan is in werkelijkheid erg variabel. De in bovenstaande figuur vermelde afstand van 363000 km is de gemiddelde afstand in het perigeum. In de volgende figuur zie je in de grafiek de werkelijke afstand in km van het middelpunt van de maan tot het middelpunt van de aarde in het jaar 2016. |
||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||
| De eerste drie
volle manen van 2016 zijn in de grafiek aangegeven met een rode stip. We
gaan er weer van uit dat er eens in de 29,53 dagen een volle maan is.
Zoals eerder vermeld waren er in 2016 precies drie supermanen. De figuur is niet nauwkeurig genoeg om de data af te lezen waarop de supermanen voorkwamen. Maar met behulp van deze figuur en de ruimere definitie voor een supermaan kan wel worden beredeneerd in welke maanden van 2016 de drie supermanen zijn voorgekomen. |
||||||||||||||||||||||||||||||||||||||||||
| 4p. | 7. | Beredeneer met behulp van de figuur in welke drie maanden er een supermaan moet zijn voorgekomen in 2016. | ||||||||||||||||||||||||||||||||||||||||
| Skūtsjesilen. | |||||||||||||||
| Elk jaar vindt in Friesland het skūtsjesilen plaats. Dit zijn zeilwedstrijden met oude vrachtschepen, skūtsjes genaamd. Er zijn twee organisaties die deze wedstrijden organiseren: de SKS en de IFKS. | |||||||||||||||
|
|
|||||||||||||||
| Voor het
jaarlijkse SKS-kampioenschap worden 11 wedstrijden gezeild, waaraan
14 skūtsjes meedoen. Voor elke wedstrijd krijgen de skūtsjes punten
in volgorde van aankomst. De winnaar krijgt 0,9 punt. Nummer twee
krijgt 2 punten, nummer drie krijgt 3 punten, enzovoort. Zie de
tabel. Na afloop van de 11 wedstrijden wordt voor elk skūtsje het slechtste resultaat geschrapt. De punten van de overige 10 wedstrijden worden per skūtsje bij elkaar opgeteld. Het skūtsje dat dan de minste punten heeft, is kampioen. |
|
||||||||||||||
| 3p. | 8. | Onderzoek of het theoretisch mogelijk is dat elk skūtsje in de einduitslag een geheel aantal punten heeft. | |||||||||||||
| De afmetingen van de deelnemende skūtsjes zijn niet identiek. Om er toch een eerlijke wedstrijd van te maken, wordt voor elk skūtsje het maximaal toegestane zeiloppervlak berekend. In eerste instantie rekende de SKS met formule Amels, maar deze formule is in 2000 aangepast en opnieuw aangepast in 2016: | |||||||||||||||
| S = 1,90 L (B + 2D) (formule Amels) | |||||||||||||||
| S = 2,15 L (B + 2D) (formule 2000) | |||||||||||||||
| S = 2,15 L (2/3B + 1,25 + 2D) (formule 2016) | |||||||||||||||
| Hierin is S het maximaal toegestane zeiloppervlak in m2, L de lengte van het skūtsje, B de breedte en D de diepgang (L, B en D in meters). De invoering van formule 2000 had tot gevolg dat elk skūtsje hetzelfde percentage extra zeil mocht hebben. | |||||||||||||||
| 2p. | 9. | Bereken het percentage extra zeil dat elk skūtsje van formule 2000 mag hebben ten opzichte van formule Amels. Geef je antwoord in hele procenten. | |||||||||||||
| Een van de skūtsjes is 17,13 m lang en 3,57 m breed en mag volgens formule 2000 een maximaal zeiloppervlak van 160,2 m2 hebben. | |||||||||||||||
| 4p. | 10. | Bereken hoeveel m2 zeiloppervlak dit skūtsje volgens formule 2016 meer mag hebben dan volgens formule 2000. Geef je antwoord in één decimaal. | |||||||||||||
| Bij de invoering van formule 2016 waren er ook skūtsjes die ten opzichte van formule 2000 minder zeil mochten hebben. Dit heeft te maken met de breedte van de skūtsjes. | |||||||||||||||
| 3p. | 11. | Onderzoek bij welke breedte van het skūtsje de invoering van formule 2016 betekent dat dit skūtsje minder zeil mag hebben dan bij formule 2000. Geef je antwoord in meters en in twee decimalen. | |||||||||||||
| Voor het
IFKS-kampioenschap worden andere regels gehanteerd voor het maximaal
toegestane zeiloppervlak. Hier wordt gebruikgemaakt van de volgende
formule: S = (3,2525 - 0,05L) L B (formule IFKS) Hierin is S het maximaal toegestane zeiloppervlak in m2, L de lengte van het skūtsje en B de breedte (L en B in meters). Voor een skūtsje met een breedte van 3,52 m en een diepgang van 0,42 m geeft formule 2016 van de SKS een zeiloppervlak dat 25 m2 groter is dan het toegestane zeiloppervlak volgens formule IFKS. |
|||||||||||||||
| 3p. | 12. | Bereken de lengte van dit skūtsje. Geef je antwoord in meters en in twee decimalen. | |||||||||||||
| Berlijnse stoel. | |||
 |
|||
| Gerrit Rietveld
(1888-1964) was een foto belangrijke kunstenaar van de kunststroming
De Stijl. In 1923 ontwierp hij de Berlijnse stoel. Zie de foto. De Berlijnse stoel bestaat uit acht houten planken. De stoel wordt nog steeds door meerdere fabrikanten gemaakt, niet altijd met dezelfde afmetingen. Hier zie je een bouwtekening, met alle afmetingen in mm. |
|||
| 4p. | 13. | Geef de minimale
(binnen)afmetingen van een doos waarin deze stoel past. Gebruik
hierbij de bouwtekening. Geef je antwoorden in hele cm. |
|
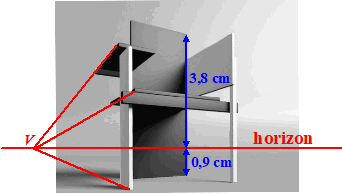
| Hieronder staat een foto van een Berlijnse stoel. Deze stoel heeft een hoogte van 106 cm. De horizon loopt op deze foto horizontaal. | |||
|
|
|||
| 4p. | 14. | Onderzoek met behulp van de foto op welke hoogte de foto genomen is. Geef je antwoord in hele cm. | |
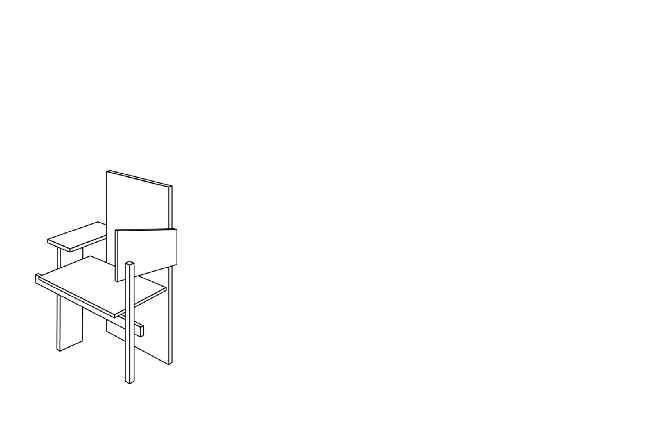
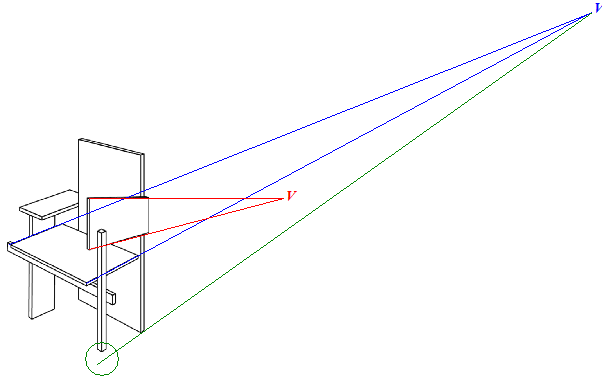
| Hieronder staat een perspectieftekening van de Berlijnse stoel. In deze tekening zijn er meerdere dingen die niet juist getekend zijn. | |||
|
|
|||
| 4p. | 15. | Noem twee dingen in de tekening die volgens de regels van het perspectief niet juist getekend zijn. Licht je antwoord toe met behulp van de figuur. | |
| Rondetijden. | |||
| Bij het langebaanschaatsen spelen rondetijden een belangrijke rol. Bij korte afstanden, zoals de 500 meter, gaat het erom zo snel mogelijk na de start een zo hoog mogelijke snelheid te krijgen en daarna die snelheid zo lang mogelijk vast te houden. Op middellange afstanden zoals de 1500 en de 3000 meter werkt dat echter niet, omdat de schaatser dan ruim voor de finish al zo vermoeid raakt dat hij haast niet meer vooruitkomt. | |||
|
|
|||
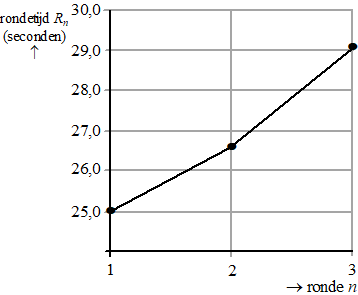
| De meeste
schaatsers rijden daarom op de middellange afstanden volgens een
schema waarbij de rondetijden steeds iets toenemen. In de figuur zie je het verloop van de rondetijden van Kjeld Nuis op de 1500 meter tijdens de Olympische Winterspelen van 2018. De 1500 meter bestaat uit een eerste deel van 300 meter en daarna nog drie volledige ronden van elk 400 meter. In de figuur staan alleen de rondetijden van de drie volledige ronden. |
|||
|
|
|||
| Kjeld Nuis werd in 2018 olympisch kampioen op de 1500 meter met een winnende eindtijd van 1.44,0 (1 minuut en 44,0 seconden). | |||
| 3p. | 16. | Bereken met behulp van de figuur zijn tijd in seconden op de eerste 300 meter. Geef je antwoord in één decimaal. | |
| In de figuur is
goed te zien dat de rondetijden van Kjeld Nuis steeds toenemen. Deze
toename per ronde wordt het verval genoemd. Je kunt bijvoorbeeld
zeggen dat het verval van Kjeld Nuis in de tweede ronde 1,6 seconden
was. Amateurschaatser Piet Versnel schaatst de 3000 meter. Deze afstand bestaat uit een eerste deel van 200 meter en daarna nog zeven volledige ronden van elk 400 meter. Hij schaatst zijn eerste volledige ronde in 40,0 seconden. Het verval is iedere ronde 0,4 seconden. De rondetijden van de volledige ronden van Piet vormen een rij. De rondetijd in seconden van de n-de volledige ronde noteren we als Rn . |
|||
| 3p. | 17. | Stel een recursieve formule op van deze rij. | |
| De directe
formule die bij de rondetijden van de volledige ronden van Piet
hoort, is: Rn = 40,0 + 0,4(n - 1) (formule 1) Uitgaande van gelijkblijvend verval per ronde, kan de eindtijd T in seconden van schaatsers worden berekend met de formule: T = E + 1/2 (R1 + Ra) a (formule 2) Hierin is E de tijd in seconden over de eerste 200 meter, R1 de rondetijd van de eerste volledige ronde, Ra de rondetijd van de laatste ronde en a het aantal volledige ronden. De tijd over de eerste 200 meter van Piet Versnel op de 3000 meter is 24,2 seconden. Daarna verlopen zijn rondetijden volgens formule 1. |
|||
| 4p. | 18. | Bereken de gemiddelde snelheid van Piet op de 3000 meter. Geef je antwoord in kilometers per uur en in één decimaal. | |
| Door flink te
trainen heeft Piet op de 3000 meter zijn tijd over de eerste 200
meter verbeterd tot 23,3 seconden. Hij schaatst zijn eerste
volledige ronde nu in 38,4 seconden en zijn verval v is
iedere ronde constant. Met behulp van deze gegevens en formule 2 kan
de volgende formule voor de eindtijd T in seconden worden
opgesteld: T = 292,1 + 21 v (formule 3) Hierin is v het verval in seconden. |
|||
| 3p. | 19. | Laat zien hoe formule 3 kan worden opgesteld. | |
| Piet wil graag het record van zijn schaatsvereniging op de 3000 meter verbeteren. Dat record staat op 4.59,5 (4 minuten en 59,5 seconden). | |||
| 4p. | 20. | Bereken met behulp van formule 3 hoe groot het verval van Piet maximaal mag zijn om het record te verbeteren. Geef je antwoord in seconden en in één decimaal. | |
| Hotelschakeling. | |||
| De lamp bij een
trap kan vaak met twee verschillende schakelaars aan- en uitgedaan
worden. In dat geval spreekt men van een hotelschakeling. Bij een
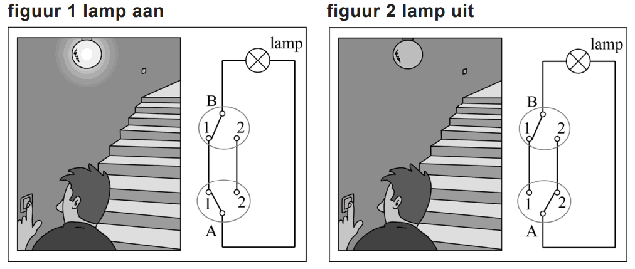
trap zit de ene schakelaar beneden en de andere boven. In de figuren 1 en 2 zijn twee mogelijke situaties weergegeven. De twee schakelaars A en B kunnen onafhankelijk van elkaar in twee standen staan: stand 1 en stand 2. De stand van de schakelaars bepaalt of er wel of geen stroom naar de lamp kan lopen en dus of de lamp wel of niet aan is. |
|||
|
|
|||
| In de situatie
van figuur 1 staan beide schakelaars in stand 1 en is de lamp aan,
omdat de stroom via schakelaar A naar schakelaar B loopt en vanaf
daar verder naar de lamp. Als de verbinding is onderbroken, is de
lamp uit. Dit zie je in figuur 2, waar schakelaar A is omgezet naar
stand 2. Als schakelaar A in stand 1 staat, noteren we dit als A1. Verder noteren we L voor de situatie dat de lamp aan is. In de situatie van figuur 1 geldt dan: (A1 ∧ B1) ⇒ L Een andere ware bewering is: (A2 ∧ B1) ⇒ ¬L |
|||
| 2p. | 21 | Vertaal deze laatste bewering in een gewone zin. | |
| In hotels wordt ook weleens gebruikgemaakt van de zogenaamde slaapkamerschakeling. Deze schakeling is bedoeld om in een hotelkamer de plafondlamp óf de lamp in de badkamer aan te doen. De twee lampen kunnen nooit gelijktijdig aan zijn. | |||
|
|
|
||
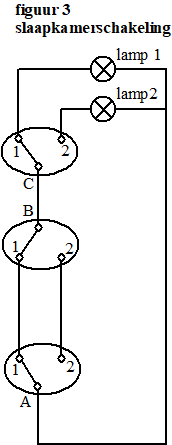
| Bij de slaapkamerschakeling wordt gebruikgemaakt van drie schakelaars. De eerste twee schakelaars (A en B) vormen samen een hotelschakeling: één bij de deur en één bij het bed. De derde schakelaar (C) wordt in de badkamer geplaatst. Deze derde schakelaar dient als keuzeschakelaar tussen de plafondlamp (lamp 1) en de lamp in de badkamer (lamp 2). In figuur 3 is dit schematisch weergegeven. We noteren L1 voor de situatie dat lamp 1 aan is en L2 voor de situatie dat lamp 2 aan is. In de situatie van figuur 3 geldt dan: (A1 ∧ B1 ∧ C1) ⇒ L1 | |||
| Er zijn twee verschillende standen van de drie schakelaars die ervoor zorgen dat lamp 2 aan is. | |||
| 3p. | 22. | Noteer die twee
manieren in logische symbolen en combineer deze vervolgens tot één
formule van de vorm: ... ⇒ L2 . |
|
| We nemen aan
dat je aan de buitenkant van een schakelaar niet kan zien of deze in
stand 1 of stand 2 staat. Verder nemen we aan dat de schakelaars
niet kapot zijn. We bekijken de volgende situatie van een slaapkamerschakeling waarin ten minste één lamp kapot is. Iemand komt een donkere hotelkamer in en zet schakelaar A om, maar beide lampen blijven uit. In dat geval is er minstens één lamp kapot. Om te achterhalen welke lamp kapot is, of dat zelfs beide lampen kapot zijn, zet zij schakelaar C om. Er zijn dan twee mogelijkheden: er is meteen duidelijk wat er aan de hand is, of er moet nog een andere schakelaar worden omgezet om te achterhalen wat er aan de hand is. |
|||
| 4p. | 23. | Beredeneer hoe je er na het omzetten van schakelaar C en eventueel nog een andere schakelaar achter kunt komen welke lamp kapot is of welke lampen kapot zijn. | |