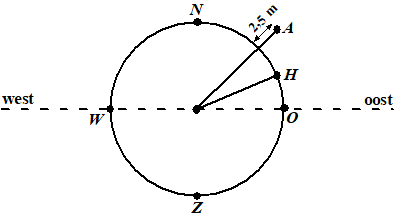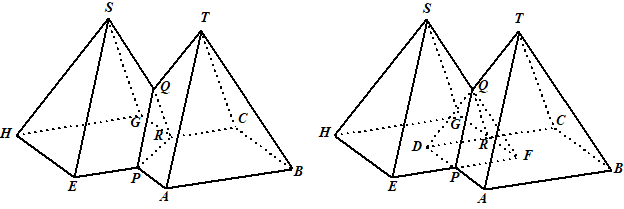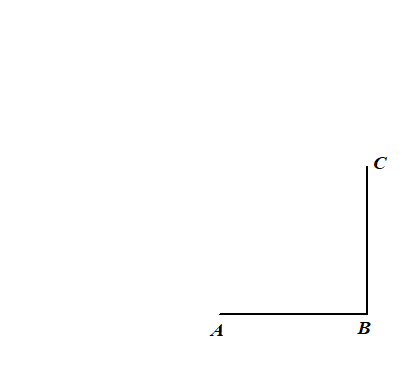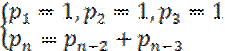VWO WC, 2021 - I

 

Draaiend huis.
       
Op de Hasseltrotonde in Tilburg staat een huis. Eigenlijk is ‘staat’ niet het goede woord, want het huis beweegt: het draait in het rond. Het gevolg is dat elke keer dat je langs de rotonde rijdt, het huis op een andere plaats kan staan. Het is een kunstproject, ontworpen door John Körmeling. Zie de fotos.
       

       
Het huis legt in 20 uur één ronde af, zodat je, als je de rotonde elke dag op hetzelfde tijdstip passeert, het huis geen twee opeenvolgende dagen op dezelfde plaats ziet.

Op een maandag staat het huis om acht uur ‘s morgens (08.00 uur) precies aan de oostkant van de rotonde. Voor het vervolg van de opgave is dit t = 0 . In onderstaande figuur is een overzicht van de situatie te zien. Het huis is in de figuur weergegeven als vierkantje en bevindt zich in punt O.
       

       
Het huis draait met de rijrichting van het verkeer mee.
       
3p. 1. Geef in de figuur de plaats aan waar het huis zich op diezelfde maandag om 20.30 uur bevindt. Licht je antwoord toe.
     

 
3p. 2. Bereken hoeveel hele weken na tijdstip t = 0 het huis zich voor het eerst weer om 08.00 uur op maandag in punt O bevindt.
   

 
De straal van de cirkel waarover het huis beweegt, is 30 meter. De afstand tussen het huis en de weg is 2,5 meter. Het oorspronkelijke idee van kunstenaar John Körmeling was om het huis in dezelfde tijd rond te laten draaien als de tijd die het de auto’s kost om de rotonde rond te rijden. Omdat de auto’s op de rotonde een grotere afstand moeten afleggen dan de afstand die het huis aflegt, hebben de auto’s dan dus een hogere snelheid. In onderstaande figuur is het draaiende huis met H aangegeven en een auto op de rotonde met A.
     

     
De kunstenaar ging ervan uit dat de auto’s met een gemiddelde snelheid van 25 km/uur op de rotonde zouden rijden. De omtrek van een cirkel bereken je met de formule:  omtrek = 2π • straal
     
4p. 3. Bereken met welke snelheid in km/uur het huis dan had moeten ronddraaien. Geef je antwoord in één decimaal.
   

  

 

Tweepiramidendak
       
Op de foto zie je een bijzonder huis: foto als basis voor het grondvlak zijn twee even grote overlappende vierkanten gebruikt. Het dak bestaat uit twee piramidevormige delen die aan elkaar vastzitten. In de linker figuur hieronder zie je een model van het dak van dit huis. In het vervolg van deze opgave kijken we naar dit model, waarbij de verbinding tussen de toppen van beide dakdelen buiten beschouwing is gelaten.
       

       
De rechter figuur laat zien hoe de linker figuur is ontstaan: ABCD.T en EFGH.S zijn twee even grote symmetrische vierzijdige piramiden. De top T ligt precies boven punt F. Verder is ∠APE = 90° . Hieronder is het begin van een bovenaanzicht van de linker figuur getekend.
       

       
4p. 4. Maak dit bovenaanzicht af.
     

 
Hieronder is een perspectieftekening van grondvlak ABCD van de voorste piramide te zien.
       

       
5p. 5. Teken het grondvlak EFGH van de achterste piramide in deze perspectieftekening
     

 
Om in te schatten hoeveel dakpannen er nodig zijn voor het dak, is het nodig om de totale oppervlakte te berekenen van alle schuine bovenvlakken van het model van het tweepiramidendak. De volgende afmetingen zijn bekend: AB = 7 m, AP = 3,5 m, AT = 6, 49 m en de afstand van T tot AB is (afgerond op twee decimalen) 5,47 m.
       
4p. 6. Bereken de totale oppervlakte van alle schuine bovenvlakken van het model van het tweepiramidendak. Geef je antwoord in een geheel aantal m2.
     

  

 

Huurprijzen in New York.
       
New York is al decennialang een van de populairste steden ter wereld om te wonen met als gevolg dat de gemiddelde prijs van huurwoningen er explosief gestegen is. In 1970 bedroeg de gemiddelde huur van een woning in New York $ 125 per maand. In 2013 was dat gestegen tot $ 917 per maand. Dat is een toename van ruim 600%.

Zo’n vergelijking is echter niet helemaal eerlijk, want de waarde van geld verandert ook. Dat heet inflatie. Sinds 1970 bedroeg de gemiddelde inflatie per jaar 3,95%. We gaan ervan uit dat sinds 1970 de huurprijzen, onafhankelijk van andere factoren, jaarlijks door de inflatie 3,95% gestegen zijn.

Door de $ 125 uit 1970 om te rekenen naar dollars uit 2013 kan je de reële gemiddelde huurstijging berekenen. De reële gemiddelde huurstijging is de procentuele stijging van de gemiddelde huurprijzen boven op de stijging als gevolg van de inflatie.

       
3p. 7. Bereken de reële gemiddelde huurstijging. Geef je antwoord in één decimaal.
     

 
In het vervolg van deze opgave zijn alle genoemde bedragen, getallen en percentages berekend met de naar 2013-dollars omgerekende bedragen. Je hoeft dus zelf geen rekening te houden met inflatie. Verder spreken we in het vervolg van deze opgave over inkomen, huurprijs en huurlast, terwijl daar gemiddeld inkomen, gemiddelde huurprijs en gemiddelde huurlast bedoeld wordt.
       
Een belangrijke maatstaf om de betaalbaarheid van huurwoningen te onderzoeken is het percentage van het inkomen dat besteed wordt aan het betalen van de huur: de huurlast.

In 1960 bedroeg de huurprijs in New York $ 561 en was de huurlast 15%. In de periode tussen 1960 en 2013 stegen de huurprijzen met 63,5%, terwijl het maandinkomen in dezelfde periode met slechts 17% steeg. Uit deze gegevens volgt dat de huurlast in 2013 ongeveer gelijk was aan 21%.
       
3p. 8 Laat een berekening zien waaruit dit blijkt.  
     

 
Doordat de huurprijzen sneller stijgen dan de inkomens, neemt de huurlast steeds verder toe: van 15% in 1960 tot 21% in 2013. Een econoom beweert dat er zich grote problemen zullen gaan voordoen als de huurlast boven de 25% uitkomt. De econoom gaat ervan uit dat de huurlast exponentieel is toegenomen sinds 1960 en dat die exponentiële stijging zich ook na 2013 voortzet.
       
4p. 9. Bereken in welk jaar de huurlast volgens deze veronderstelling voor het eerst groter is dan 25%.
     

 
In de figuur hieronder is het werkelijke verloop van de huurprijs in New York en van het inkomen van zijn inwoners als percentage van de bedragen in 1960 uitgezet tegen de tijd.
       

       
Hieronder staan twee uitspraken die gaan over de gegevens in de figuur:
1. In de periode 1960–1980 steeg de huurprijs sneller dan in de periode 1980–2000.
2. In de periode 1990–2000 daalde de huurlast.
       
4p. 10. Leg voor elk van deze uitspraken uit of deze waar is of niet.
   

 

     
In de figuur hierboven is te zien dat de huurprijs schommelt om een trendlijn. De huurprijs kan dus worden benaderd met behulp van deze trendlijn.

In 1960 bedroeg de huurprijs in New York $ 561 en was de huurlast 15%.

Het gemiddelde maandinkomen van de inwoners van New York was op zijn hoogst in het jaar 2000 en was toen $ 4832. In een rapport van de Bank of America uit 2013 stond dat het gemiddelde maandinkomen pas in 2023 weer op het niveau van het jaar 2000 zou zijn.

Je kunt nu, uitgaande van de getekende trendlijn voor de huurprijs en de veronderstelling uit het rapport van de Bank of America, berekenen wat in 2023 de huurlast in New York zal zijn.
     
5p. 11. Bereken met behulp van deze trendlijn en de genoemde veronderstelling de huurlast in New York in 2023. Geef je antwoord in één decimaal.
   

  

 

De Grand Prix van Monaco
       
Op 19 mei 1996 werd in Monaco de Grand Prix Formule 1 de Monaco gehouden. Deze race staat in de autosport bekend als de race met de meeste uitvallers ooit. Aan deze race namen 22 coureurs deel, van wie er uiteindelijk slechts drie de finish haalden.
       
3p. 12. Bereken hoeveel verschillende top 3’s er mogelijk zijn in een wedstrijd met 22 deelnemers.
     

 
De race duurde 75 ronden van 3328 meter en werd gewonnen door de Fransman Olivier Panis.

Panis deed in totaal 2 uur en 45 seconden over de race.
       
3p. 13. Bereken zijn gemiddelde snelheid. Geef je antwoord in hele kilometers per uur.
     

 
De uitslag van de race staat in de tabel. Bij de uitgevallen coureurs staat aangegeven of ze uitvielen door een ongeluk (O), door technische problemen (T) of door een stuurfout (S).
       
positie naam  
1 O. Panis -
2 D. Coulthard -
3 J. Herbert -
4 H. Frentzen T
5 M. Salo O
6 M. Häkkinen O
7 E. Irvine O
- J. Villeneuve O
- J. Alesi O
- L. Badoer O
- D. Hill T
 
positie naam  
- M. Brundle S
- G. Berger T
- P. Diniz T
- R. Rosset S
- U. Katayama S
- R. Barrichello S
- M. Schumacher O
- P. Lamy O
- G. Fisichella O
- J. Verstappen O
- A. Montermini T
       
Ondanks dat Frentzen, Salo, Häkkinen en Irvine uitgevallen zijn, hebben ze toch een positie in de eindstand toebedeeld gekregen, omdat ze tenminste 90% van de te racen afstand hebben afgelegd. Deze posities zijn op volgorde van het aantal afgelegde ronden. Als dat aantal gelijk is, wordt gekeken naar wie als eerste over de finish kwam aan het einde van die ronde.

Bij iedere race in een Formule 1-seizoen kunnen de coureurs punten verdienen voor het kampioenschap. Bij de race in 1996 gold de regel dat de eerste 6 coureurs punten kregen, de overige 16 coureurs niet. Het was dus mogelijk dat een uitgevallen coureur toch punten behaalde.

In het diagram in de figuur zijn alle mogelijkheden voor de coureurs schematisch weergegeven.
       

       
In dit diagram geldt:
- A zijn de coureurs die punten hebben behaald.
- B zijn de coureurs die zijn uitgevallen.
- C zijn de coureurs die zijn uitgevallen door een ongeluk.
- D zijn de coureurs die zijn uitgevallen door technische problemen.
       
Het ingekleurde deel van het diagram kan maar één coureur bevatten.
       
2p. 14. Leg uit welke coureur dat is.
     

 
Er is ook één gebied in het diagram dat helemaal leeg blijft bij de race in Monaco.
       
2p. 15. Geef in de figuur aan welk gebied dat is.  
     

 
We kunnen de positie van een coureur in het diagram ook beschrijven met behulp van logische symbolen. Er geldt:
a : ‘de coureur’ bevindt zich in gebied A.
b : ‘de coureur’ bevindt zich in gebied B.
c : ‘de coureur’ bevindt zich in gebied C.
d : ‘de coureur’ bevindt zich in gebied D
       
Als bijvoorbeeld ‘de coureur’ zou verwijzen naar een coureur in het ingekleurde gebied, dan geldt a ∧ d.
       
2p. 16. Beredeneer naar welke coureurs ‘de coureur’ allemaal zou kunnen verwijzen als geldt  b ∧ ¬ (c ∨ d).
     

 
2p. 17. Geef in logische symbolen de situatie weer dat ‘de coureur’ verwijst naar M. Schumacher.
     

  

 

Padovantafels
       
Op de foto zie je een zogenoemde foto Fibonaccitafel van de firma NautaBene Design. Het patroon van het tafelblad is geïnspireerd op de rij van Fibonacci: 1, 1, 2, 3, 5, 8, 13, 21,….

Het tafelblad bestaat uit vier vierkanten en een rechthoekig gat. De zijden van de vierkanten verhouden zich als 5 : 8 : 13 : 21.
De tafel is 120 cm lang en 74 cm breed.
     
3p. 18. Bereken de afmetingen van het rechthoekige gat. Je mag hierbij de randen om de vierkanten buiten beschouwing laten. Geef je antwoord in een geheel aantal cm.
     

 
Behalve de rij van Fibonacci bestaan er ook andere rijen, bijvoorbeeld de rij van Padovan. In onderstaande figuur zie je het ontwerp voor een Padovantafel. Het tafelblad bestaat uit zes gelijkzijdige driehoeken met zijden van 2, 2, 3, 4, 5 en 7 dm. In het tafelblad zit een gat. Hier zijn drie gelijkzijdige driehoekjes met een zijde van 1 dm weggelaten.
       

       
Het patroon van het tafelblad is geïnspireerd op de rij van Padovan, een rij getallen die op de volgende manier beschreven kan worden:

       
De tweede regel zegt dat   p4 =  p2  + p1,    p5 =  p3 + p2, enzovoort.
Zo ontstaat dus de rij getallen: 1, 1, 1, 2, 2, 3, 4, 5, 7,… Deze rij kan nog verder voortgezet worden.

In onderstaande figuur zie je nogmaals het ontwerp voor de Padovantafel, waarvan pn de lengte van de zijde van de n-de driehoek is. Bij een zijde van elke driehoek is de bijbehorende term pn uit de rij van Padovan gezet.
       

       
In deze figuur is te zien dat vanaf p6 het volgende geldt:
p6 = p5 + p1         (1)
p7 = p6 + p2         (2)
p8 = p7 + p3         (3)
enzovoort.

Blijkbaar kunnen de Padovan-getallen vanaf p6 ook op deze manier berekend worden.
       
2p. 19. Geef een recursieve formule (inclusief startwaarden) die bij deze manier hoort.
     

 
Op grond van de formule  p = pn - 2 + pn - 3 aan het begin van deze opgave geldt dus:
p4 = p2 + p1         (4)
p5 = p3 + p2         (5)
p6 = p4 + p3         (6)
       
2p. 20. Toon aan, door uit te gaan van de formules 4, 5 en 6, dat geldt:  p6 = p5 + p1. Doe dit zonder een getallenvoorbeeld te gebruiken.
     

  

 

De Wisselslag.
       
Zwembad De Wisselslag in Blerick (Limburg) heeft drie binnenbaden, waaronder een wedstrijdbad met een inhoud van 647 m3, en een buitenbad.

Om een zwembad te vullen kunnen er verschillende types pompen gebruikt worden. Hoe verder een pomp van het zwembad af staat, hoe meer tijd het kost om het zwembad te vullen. In onderstaande figuur is voor vier verschillende pompen de hoeveelheid water die een pomp per uur kan vullen (Q) in m3 per uur uitgezet tegen de afstand van de pomp tot het zwembad (A) in meters.
       

       
Het wedstrijdbad van De Wisselslag wordt gevuld met behulp van een pomp van type SB15 op 8 meter afstand. Als de medewerkers op diezelfde afstand een pomp van type SB20 zouden gebruiken, zou er minder tijd nodig zijn om het zwembad te vullen.
       
4p. 21. Bereken met behulp van de figuur hoeveel tijd er dan minder nodig zou zijn om het zwembad te vullen. Geef je antwoord in een geheel aantal minuten.
     

 
4p. 22. Schat met behulp van de grafiek die hoort bij een pomp van het type SB10  de waarde van de helling van de grafiek bij A = 10 en leg uit wat de betekenis is van deze waarde. Geef de waarde van de helling in één decimaal.
     

 
De bezoekersaantallen van het buitenbad van zwembad De Wisselslag lopen terug. Daardoor dreigt het buitenbad gesloten te worden. Dit teruglopen van bezoekersaantallen van zwembaden is een landelijk probleem, met name in buitenbaden. Zie onderstaande tabel.
       
jaartal 1988 1991 1994 1997 2000 2003 2006 2009 2012
aantal
buitenzwembaden		 334 290 260 245 265 250 225 225 200
aantal bezoekers
per buitenzwembad
× 1000		 37 44 52 49 39 52 49 43 33
       
Je ziet in de tabel dat in de periode tussen 2003 en 2012 zowel het aantal buitenzwembaden als het aantal bezoekers per buitenzwembad afneemt. Ook het totale aantal bezoekers zal dus vanaf 2003 afnemen.
       
3p. 23. Onderzoek of het totale aantal bezoekers van buitenzwembaden in de periode tussen 2003 en 2012 exponentieel afneemt.
     

 
Een deskundige beweerde in 2012 dat het zeer waarschijnlijk was dat het aantal buitenzwembaden in de jaren na 2012 zou blijven dalen tot één buitenzwembad per twee gemeenten. In 2019 telde Nederland 355 gemeenten.
       
3p. 24. Onderzoek met behulp van lineair extrapoleren of de deskundige in 2019 al gelijk heeft gekregen.
     

 
       

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
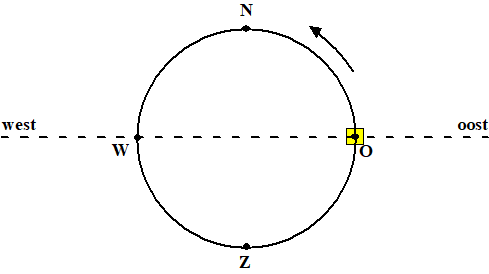
1. 20:30 is 12,5 uur na 8:00 uur
Een hele rondgang kost 20 uur, dus er is 12,5/20 = 5/8 deel van een rondgang gemaakt.
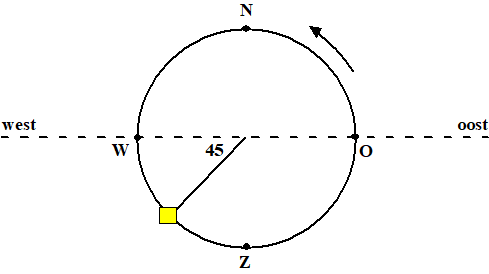
Er is dus 5/8 deel van de cirkel afgelegd, en dan staat het huis als in de figuur hieronder (midden tussen W en Z).
 

   
2. Het huis is weer om 8:00 uur op de Oostplaats als een aantal keer 20 gelijk is aan een aantal keer 24.
Dat is voor het eerst zo bij zo bij 6 * 20 = 120 = 5 * 24
Dus steeds na 120 uur = 5 dagen is het huis weer om 8:00 op de Oostplaats.
Dat wordt dan op de dagen (steeds 5 dagen later): ma - za - do - di - zo - vr - wo - ma
na 7 series van 5 dagen is het huis op maandag weer om 8:00 op de oostplaats.
Dat is dus 5 weken.
   
3. De auto's leggen in één rondje 2π • 32,5 = 204,2035...  meter af = 0,204...  km
Met 25 km/uur kost dat  0,204.../25 = 0,00816... uur.
Het huis legt in één rondje 2π • 30 = 188,4955... m = 0,18849... km af
Als dat in 0,00816,,, uur gebeurt is de snelheid  0,18849.../0,00816 = 23,1 km/uur
   
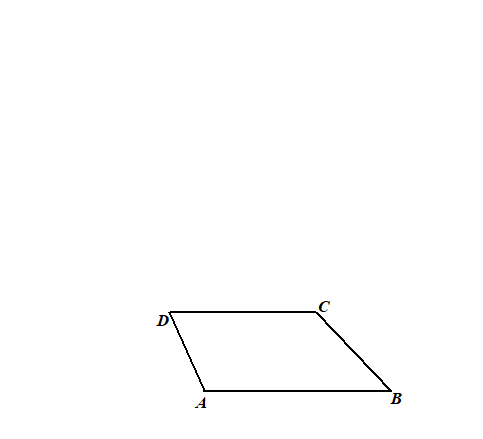
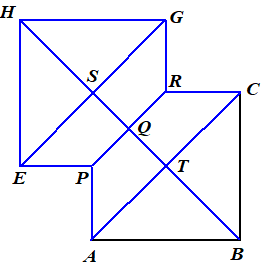
4. Teken eerst het hele vierkant ABCD.
Teken ook het hele vierkant EFGH
Teken HB en PR en AC en EG

Veeg daarna het vierkant DPFR weer uit.

Dat geeft de figuur hiernaast.
 
     
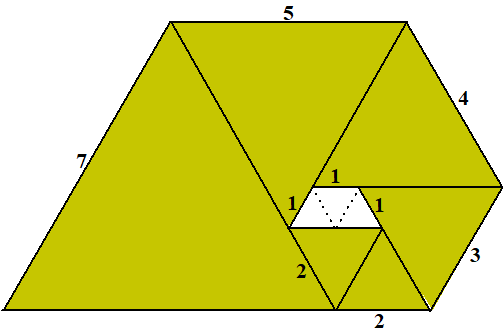
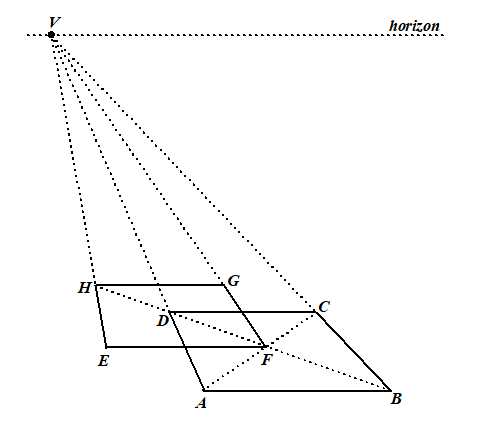
5. Teken het snijpunt V
van BC en AD

Teken snijpunt F  van BD en AC

Teken FE evenwijdig aan AB en zo dat DA door het midden ervan gaat,

Teken EV en FV

Teken het snijpunt H van het verlengde van BD met EV

Teken HG evenwijdig aan AB

Klaar.
Zie hiernaast (de stippellijnen zijn hulplijnen)


 
   
6. De oppervlakte van driehoek ABT is 0,5 • 7 • 5,47 = 19,145
De oppervlakte van driehoek PFQ is 0,5 • 3,5 • 0,5 • 5, 47 = 4,78...
De oppervlakte van vierhoek EPQS is 19,145 -  4,78... = 14,3...
De totale oppervlakte is 4 • 19,145 +  4 • 14,3... =134,0 dus dat is ongeveer 134 m²
   
7. 3,95% toename betekent een groeifactor van 1,0395
in 43 jaar (van 1970 naar 2013)   is dat een factor  (1,0395)43 = 5,2899....
125 dollar is na 43 jaar dus  125 • 5,2899 = 661,245....
de reële huurstijging is dus  917 - 661,245.... = 255,75...
Dat is  255,75.../661,245... • 100% = 38,7%
   
8. Het maandinkomen in 1960 was  561/0,15 = 3740
In 2013 was het maandinkomen 17% hoger, dus 1,17 • 3740 = 4375,8
De huur was in 2013 vanaf 561 met 63,5% gestegen dus gelijk aan 1,635 • 561 = 917,235
De huurlast was dus 917,235/4375,8 = 0,209  dat is dus 20,9%  dus ongeveer 21%
   
9. Er is een toename met factor 21/15 = 1,4 in 53 jaar.
Voor de factor per jaar geldt dus  g53 = 1,4  dus  g = 1,41/53 = 1,00636....
Als het 25 is geworden dan geldt dus  15 • 1,00636t = 25
1,00636t = 1,666...
t = log(1,666...)/log(1,00636...) = 80,4
Dat is dus in 2041
   
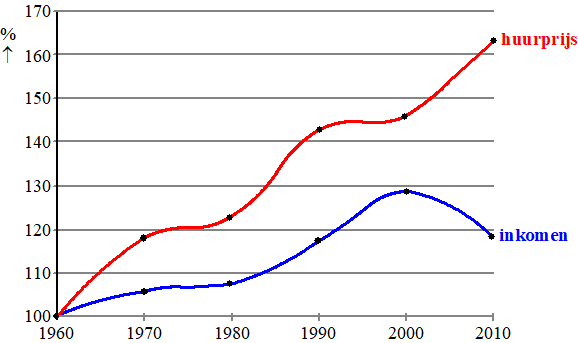
10. De helling van het verbindingslijnlijnstuk tussen de stippen van 1960 en 1980 is ongeveer gelijk aan de helling van het verbindingslijnstuk lijnstuk tussen 1980 en 2000. (want de 3 stippen liggen ongeveer op één lijn)
Dus de stijging was ongeveer gelijk.
Uitspraak 1 is dus NIET WAAR

Tussen 1990 en 2000 stijgen de huren niet terwijl het inkomen sterk toeneemt.
Dan neemt de huurlast af, dus uitspraak 2 is WAAR.
   
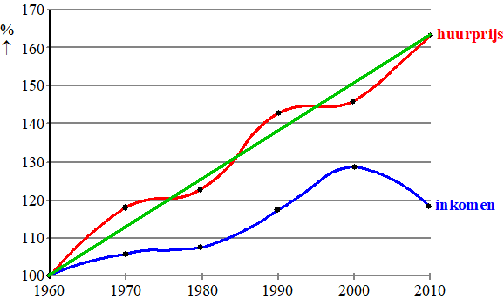
11. Lees twee punten af op de trendlijn, bijvoorbeeld:  (1960, 100)  en  (2000, 150)
De helling daartussen is  (150 - 100)/(2000 - 1960) = 1,25
Neem 1960 als t = 0, dan is de vergelijking van de trendlijn  P = 1,25t + 100
2023 is dan t = 63, dus dan is  P = 1,25 • 63 + 100 = 178,75
De huurprijs in 2023 is dan 1,7875 • 561 = 1002,79
1002,79/4832 • 100% = 20,8%
   
12. nummer 1 kan op 22 manieren
daarna nummer 2 nog op 21 manieren
daarna nummer 2 nog op 20 manieren
in totaal 22 • 21 • 20 = 9240 manieren.
   
13. De totale raceafstand was 75 • 3328 = 249600 meter
de totale tijd was 2 uur en 45 seconden en dat is   2 • 3600 + 45 = 7245 seconden
verhoudingstabel:
 
seconden 7245 3600
meters 249600 ??
  ?? = 3600 • 249600/7245 = 124024 meter dus dat is  124 km/uur
   
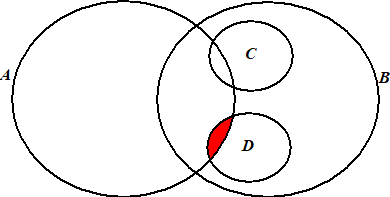
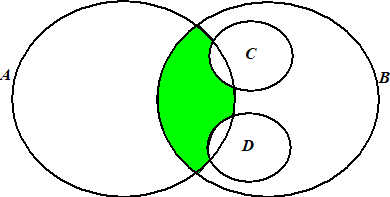
14. Het ingekleurde gebied ligt binnen A en binnen D
Dat is dus een coureur die door technische problemen is uitgevallen  (D) maar die wel punten heeft behaald  (A)
In de tabel een coureur met en T en wél een eindpositie.
Dat is H. Frentzen.
   
15. De enige coureurs die uit zijn gevallen maar wel punten hebben behaald zijn door een technische probleem (T) of door een ongeluk (O). Die liggen dus allemaal in C of D
Dus de overlap van A en B die NIET binnen C of D ligt komt niet voor
   
 

   
16. b ∧ ¬ (c ∨ d).
b :  wel uitgevallen
¬ (c ∨ d):  niet na een technisch probleem of een ongeluk
Dus de coureurs die WEL zijn uitgevallen maar NIET na een technisch probleem of een ongeluk.
Dus de coureurs die zijn uitgevallen an een stuurfout.
Dat zijn M. Brundle, R. Rosset, U. Katayama en R. Barrichello
   
17. Schumacher is uitgevallen na een ongeluk:  c
Schumacher heeft geen punten behaald:  ¬ a
Dus:    c ∧ ¬ a
   
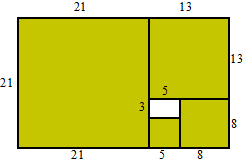
18. Zie de afmetingen hiernaast.
Het gat is 5 : 3
De totale lengte is 21 + 13 = 34 en die hoort bij lengte 120 cm

Dus 5 hoort bij 5/34 • 120 = 17,6
3 hoort bij 3/34 • 120 = 10,6

  Opmerking:
De tafel is 120 bij 74 en dat klopt niet: dat zou in verhouding 34 : 21 moeten zijn. (bijvoorbeeld 120 bij 74,117...)
Als je 21 in plaats van 34 neemt krijg je andere getallen.
Dat komt misschien door de ruimte tussen de vierkanten....???
   
19. pn = pn - 1 + pn - 5 
Omdat er n - 5 in deze recursievergelijking voorkomt moeten er ook 5 startwaarden gegeven worden, dus:
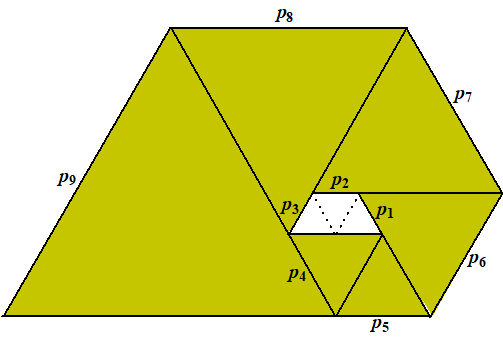
p1 = p2 = p3 = 1 en p4 = p5 = 2
   
20. p6 = p4 + p3
p4 = p2 + p1
Daaruit volgt dat  p6 = (p2 + p1) + p3 = p1 + p2 + p3
maar p2 + p3 = p5
Dus p6 = p1 + (p2 + p3) = p1 + p5
   
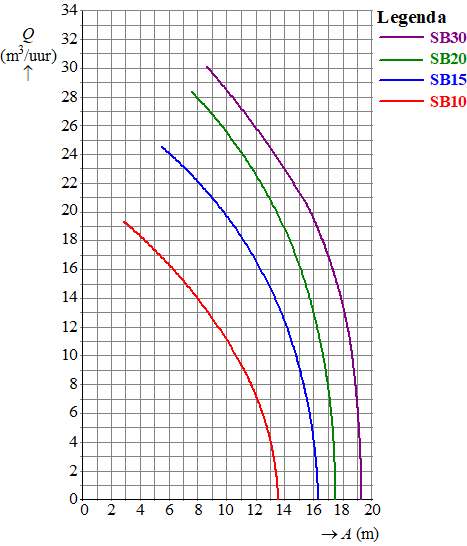
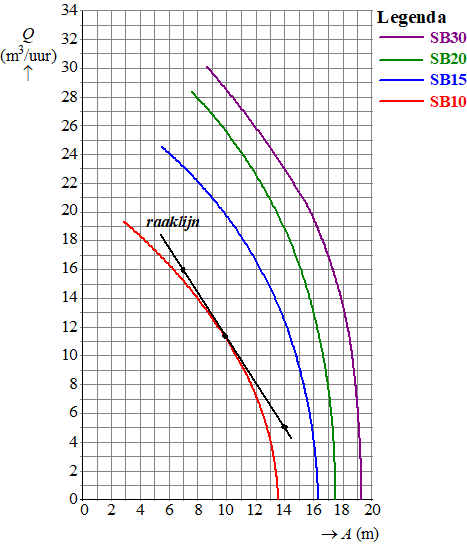
21. aflezen: 
bij 8 meter geeft SB15 dat Q = 22 m3/uur,  dus met SB15 duurt het 647/22 = 29,40...uur
bij 8 meter geeft SB10 dat Q = 28 m3/uur, dus met SB20 duurt het 647/28 = 23,10...uur

Dat scheelt 29,40... - 23,10... = 6,301948...uur
0,301948 • 60 minuten = 18,116... minuten
Het scheelt dus 6 uur en 18 minuten.
   
22. De raaklijn is hiernaast getekend en gaat bijv. door de punten (14, 5) en (7, 16)

de helling is dan
(16 - 5)/(7 - 14)
= 11/-7 = -1,6

Dat is dus ook de helling van de grafiek van SB10 in A = 10

Betekenis:
op afstand 10 m van het zwembad geldt:
met elk meter die de pomp verder van het zwembad afstaat vermindert het aantal m3 dat de pomp kan vullen met 1,5
   
23. Voeg een rij met totalen toe (aantal zwembaden * aantal bezoekers per zwembad)
 
jaartal 2003 2006 2009 2012
aantal
buitenzwembaden		 250 225 225 200
aantal bezoekers
per buitenzwembad
× 1000		 52 49 43 33
totaal 13000 11025 9675 6600
  Het is steeds een periode van 3 jaar, dus je hoeft alleen te kijken of de vermenigvuldigingsfactoren (ongeveer) gelijk zijn.
11025/13000 = 0,848
9675/11025 = 0,878
6600/9675 = 0,682
Dat is niet gelijk dus de afname is niet exponentieel.
   
24. Tussen 2009 en 2012 daalde het aantal met 25
Dat is per jaar  25/3 = 8,33...
tussen 2012 en 2019 is 7 jaar.
Het zou dan met 7 • 8,33... = 58,3... dalen
Dan zouden er in 2019 nog 200 - 58,33... = 141 á 142 zwembaden zijn.
355 gemeenten betekent 355/2 = 177 à 178 zwembaden
Het aantal zwembaden dat met extrapolatie is berekend is lager dan het aantal door de deskundige voorspeld.
Of:  het aantal van slechts 1 zwembad per twee gemeenten is al eerder behaald dan de deskundige voorspelde
(het woordje "al" in de vraag vind ik een beetje dubieus...)