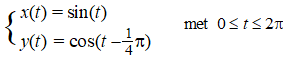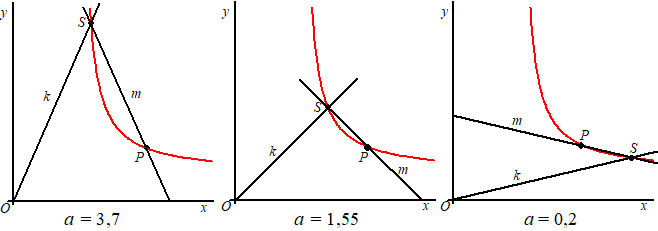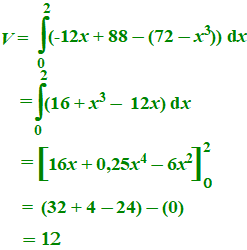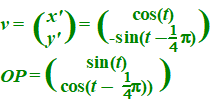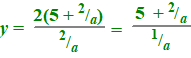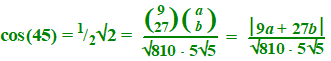Nieuwe pagina 1

Twee functies.

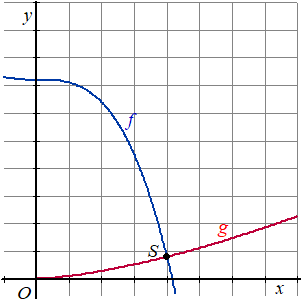
De functies f en g worden gegeven door f(x) = 72 - x³ en g(x) = x√x Het snijpunt van de grafieken van f en g is het punt S. Zie de figuur.



4p.	1.	Bereken exact de coördinaten van S.

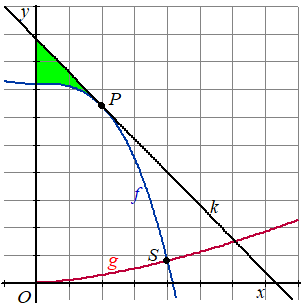
De lijn k heeft vergelijking y = -12x + 88 Lijn k raakt aan de grafiek van f in het punt P rechts van de y-as. Het vlakdeel V wordt ingesloten door de grafiek van f , lijn k en de y-as. In onderstaande figuur is dit vlakdeel groen gekleurd weergegeven.



5p.	2.	Bereken exact de oppervlakte van V.

Cobb-Douglas productiefunctie.

De Cobb-Douglas-productiefunctie is een wiskundig model dat economen gebruiken om de productie Y te voorspellen. In dit model hangt de productie af van twee factoren: arbeid en kapitaal. Met arbeid L wordt het aantal voltijdbanen van werknemers bedoeld. Met kapitaal K wordt in deze opgave het aantal machines bedoeld dat beschikbaar is voor de productie. De formule bij dit model luidt: Y = A · L^a · K^b Hierbij zijn A, a en b constanten die afhangen van het soort bedrijf. Iemand wil €1000000 per jaar investeren in een nieuw bedrijf. Voor een bedrijf in deze sector geldt A = 40, a = 0,7 en b = 0,3. De kosten per voltijdbaan per jaar bedragen €50000 en de kosten per machine per jaar bedragen €20000. Er geldt dus: 50000L + 20000K = 1000000 Uit deze gegevens is af te leiden dat: Y = 40 · L^0,7 · (50 - 2,5L)^0,3

2p.	3.	Toon aan dat Y = 40 · L^0,7 ·(50 - 2,5L)^0,3

De investeerder wil het volledige bedrag van €1000000 investeren in arbeid en kapitaal, en wel in zo'n verhouding dat de productie Y maximaal is.

5p.	4.	Bereken algebraïsch hoeveel voltijdbanen de investeerder moet inzetten om de productie Y maximaal te krijgen.

Als b = 1 - a dan spreken economen van een constant schaalvoordeel. Dat wil zeggen dat de inzet van arbeid en kapitaal evenredig is met de productie. Ofwel: als zowel L als K met dezelfde factor g groeit, dan groeit ook de productie Y = A · L^a · K^bmet diezelfde factor g.

4p.	5.	Bewijs dat bij b = 1 - a geldt: als zowel L als K met dezelfde factor g groeit, dan groeit ook de productie Y met diezelfde factor g.

Loodrecht op de snelheidsvector

De beweging van een punt P wordt gegeven door de volgende bewegingsvergelijkingen:



In de figuur hiernaast is de baan van P weergegeven. Punt A (0, ½√2) is het snijpunt van de baan van P met de positieve y-as. Er is een positie van punt P waarvoor de afstand tussen de punten A en P maximaal is.

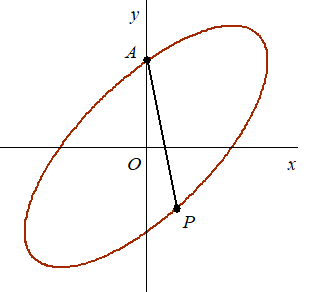3p.	6.	Bereken deze maximale afstand. Geef je eindantwoord in twee decimalen.

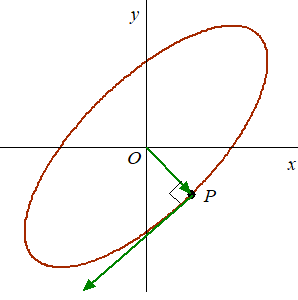
In de figuur hiernaast is een situatie weergegeven waarbij de vector OP loodrecht staat op de snelheidsvector in punt P. Hieruit volgt sin(2t) = sin(2t - ½p)

4p.	7.	Bewijs dat uit het feit dat de vector OP loodrecht staat op de snelheidsvector in punt P inderdaad volgt: sin(2t) = sin(2t - ½p)

Er zijn vier posities van P waarbij een situatie zoals in deze figuur voorkomt.

3p.	8.	Bereken exact de vier waarden van t die horen bij deze posities.

Passende parabool.

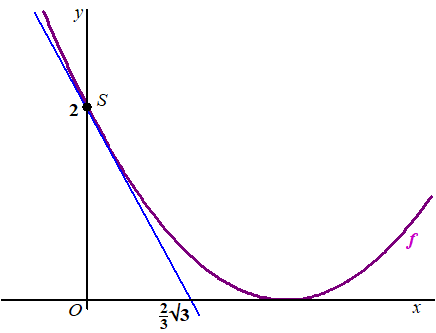
De kwadratische functie f wordt gegeven door f(x) = ax² + bx + c De grafiek van f snijdt de y-as in het punt S(0, 2). De raaklijn aan de grafiek van f in punt S snijdt de x-as in het punt (²/₃√3, 0). Verder is gegeven dat de grafiek van f een dalparabool is die de positieve x-as raakt. Zie de figuur.

6p.	9.	.Bereken exact de waarden van a, b en c.

Lijnenparen

De lijn k heeft vergelijking y = ax met a > 0. De lijn m heeft richtingscoëfficiënt –a en gaat door het punt P(10, 4) . Het punt S is het snijpunt van de lijnen k en m. Punt S ligt op de grafiek van de functie f die wordt gegeven door


waarbij geldt: x > 5 In onderstaande figuur is voor drie waarden van a de situatie weergegeven. De grafiek van f is rood weergegeven.



4p.	10.	Bewijs dat voor elke positieve waarde van a punt S op de grafiek van f ligt.

3p.	11.	Bewijs dat de grafiek van f voor elke waarde van x > 5 daalt.

Het is voor iedere waarde van a mogelijk om een cirkel c door de punten O, S en P te tekenen. Hierbij wordt de situatie dat S en P samenvallen buiten beschouwing gelaten. De coördinaten van S zijn:


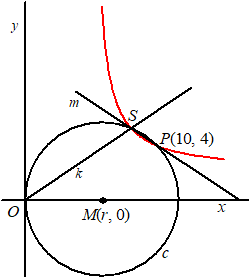Er is één waarde van a waarvoor deze cirkel raakt aan de y-as. Het middelpunt M(0, r) van deze cirkel ligt op de x-as. Deze situatie is in de figuur hiernaast weergegeven.

6p.	12.	Bereken de waarde van a waarvoor de cirkel raakt aan de y-as. Rond je eindantwoord af op twee decimalen.

Absolute logaritme

De functie f₁₈ wordt gegeven door: f₁₈(x) = \|²log(x² - 18x + 69) \| De grafiek van f₁₈ snijdt de lijn met vergelijking y = 2 in vier punten

4p.	13.	Bereken exact de x-coördinaten van deze vier punten.

De functie f_a wordt gegeven door f_a(x) = \|²log(x² - ax + 69) \| net a > 0. Voor een bepaalde waarde van a heeft de grafiek van f_a twee verticale asymptoten met een onderlinge afstand van 20.

4p.	14.	Bereken exact deze waarde van a.

Lijnstukken bij een exponentiële functie.

De functie f_a wordt gegeven door: f_a(x) = e^ax met a > 0. De lijn k met vergelijking y = e snijdt de grafiek van f_a in S. In figuur hiernaast zijn voor een waarde van a de grafiek van f_a en lijn k weergegeven. Ook is de raaklijn aan de grafiek van a door S weergegeven.

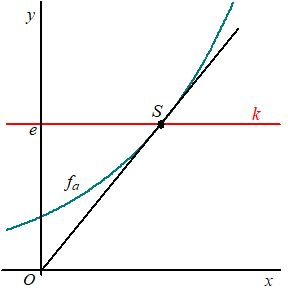5p.	15.	Bewijs dat deze raaklijn voor elke waarde van a door de oorsprong gaat.

In de figuur hiernaast is opnieuw voor een waarde van a de grafiek van f_a weergegeven. Op deze grafiek liggen de punten A(0,1), B(1, e^a) C(2, e^2a). Ook is de grafiek van de inverse van a (gestippeld) weergegeven. De punten D, E en F zijn de beeldpunten van respectievelijk A, B en C bij spiegeling in de lijn y = x . Er is een waarde van a waarvoor geldt: AD + BE = CF.

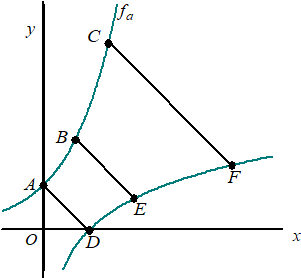7p.	16	Bereken exact deze waarde van a.

Een hoek van 45 graden.

Gegeven zijn het punt P met coördinaten (9, 27) en de vector OP . Ook zijn gegeven het punt Q(a, b) en de vector OQ Voor vector OQ geldt: \| OQ \|= 5Ö5 Er zijn twee mogelijke posities van Q, zodat geldt: ∠(OP, OQ) = 45°

6p.	17.	Bereken algebraïsch de mogelijke coördinaten van beide posities.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.	72 - x³ = x√x 72 - x³ = x^1,5 noem x^1,5 = p dan staat er 72 - p² = p p² + p - 72 = 0 (p - 8)(p + 9) = 2 p = 8 ∨ p = -9 x√x = 8 ∨ x√x = -9 dat geeft de oplossing x = 4 Het snijpunt is (4, 8)

2.	Voor punt P geldt: f '(x_P) = -12 f '(x) = -3x² = -12 dat geeft x² = 4 x_P = 2


3.	50000L + 20000K = 1000000 5L + 2K = 100 K = 50 - 2,5L substitueren in Y: Y = 40 · L^0,7 · (50 - 2,5L)^0,3

4.	Y = 40 · L^0,7 ·(50 - 2,5L)^0,3 De afgeleide moet nul zijn. Gebruik de productregel: Y ' = 40·0,7 ·L^-0,3 ·(50 - 2,5L)^0,3 + 40·L^0,7 ·0,3 ·(50 - 2,5L)^-0,7 ·-2,5 = 0 28 · L^-0,3(50 - 2,5L)^0,3 - 30 · L^0,7(50 - 2,5L)^-0,7= 028 · L^-0,3(50 - 2,5L)^0,3 = 30 L^0,7 (50 - 2,5L)^-0,7 vermenigvuldig met L^0,3dat geeft28(50 - 2,5L)^0,3 = 30L(50 - 2,5L)^-0,7vermenigvuldig met (50 - 2,5L)^0,7 dat geeft 28(50 - 2,5L) = 30L 1400 - 70L = 30L L = 14

5.	Y = A · L^a · K^{1 - a} vervang L door gL en K door gK dat geeft Y_nieuw = A · (gL)^a · (gK)^{1 -}^a Y_nieuw = A · g^aL^a ·g^{1 -}^a K^{1 -} ^a Y_nieuw = A · L^a · K^{1 -}^a · g^a · g^{1 -}^a Y_nieuw = Y_oud · g^a · g^{1 -}^a Y_nieuw = Y_oud · g¹ Y_nieuw = gY_oud

6.	Het gaat om de afstand tussen twee punten: A(0, ¹/₂√2) en P(sin(t), cos(t - ¹/₄p) Die afstand D kun je met Pythagoras berekenen: D = √( (sin(t) - 0)² + (cos(t - ¹/₄p) - ¹/₂√2)² ) Voer deze formule in bij Y1 van de GR en gebruik calc - maximum. Dta geeft maximale afstand ongeveer 1,88.

7.
	Die staan loodrecht op elkaar als hun inproduct nul is Dat geeft: cos(t)sin(t) - sin(t - ¹/₄p)cos(t - ¹/₄p) = 0 Gebruik nu sin(2t) = 2sin(t)cos(t) dus sin(t)cos(t) = ¹/₂sin(2t) Dan staat er: ¹/₂sin(2t) - ¹/₂sin(2(t - ¹/₄p)) = 0 sin(2t) = sin(2t - ¹/₂p))

8.	sin(2t) = sin(2t - ½p) 2t = 2t - ½p + k2p ∨ 2t = p - (2t - ½p) + k2p 0 = -¹/₂p + k2p ∨ 4t = ³/₂p + k2p de eerste heeft geen oplossing. De tweede geeft t = ³/₈p + k¹/₂p De oplossingen tussen 0 en 2p zijn t = ³/₈p, ⁷/₈p, ¹¹/₈p en ¹⁵/₈p

9.	De grafiek gaat door (0, 2) dus c = 2 f(x) = 0 heeft maar één oplossing (want de grafiek raakt de x-as) dus de discriminant van deze vergelijking is nul. b² - 8a = 0 ....(1) f (x) = 2ax + b dus f '(0) = b De raaklijn is de lijn y = bx + 2 y = 0 geeft dan b = -²/_x en omdat x gelijk is aan ²/₃√3 geldt dus b = -√3 Dan geeft vergelijking (1) dat a = ³/₈

10.	k: y = ax met a > 0. m: y = -ax + b door (10, 4) 4 = -19a + b geeft b = 4 + 10a dus m: y = -ax + 10a + 4 snijpunt van beide lijnen: ax = -ax + 10a + 4 2ax = 10a + 4 x = 5 + ²/_a en dan is y = ax = 5a + 2 S = (5 + ²/_a, 5a + 2) y = ^2x/_{(x - 5)} x = 5 + ²/_a geeft dan:

	teller en noemer vermenigvuldigen met a geeft inderdaad y = 5a + 2

11.	afgeleide met de quotiëntregel:

	teller is negatief noemer is een kwadraat dus altijd positief dus de afgeleide is negatief dus de grafiek daalt.

12.	Als S, P en O alle drie op de cirkel liggen dan moet gelden MO = MP = MS = r MO = MP geeft r = √((10 - r)² + 16) r² = 100 - 20r + r² + 16 20r = 116 r = 5,8 MS = 5,8 S= (x, ^2x/_{(x - 5)}) en M = (5,8, 0) Pythagoras: (x - 5,8)² + (^2x/_{(x - 5)})² = 5,8² Gebruik de GR. Intersect geeft x = 7,95.... Dan is S = ^15,90/_2,95 = 5,39 Dan is a = ^5,39/_7,95 = 0,68

13.	\|²log(x² - 18x + 69) \| = 2 ²log(x² - 18x + 69) = 2 ∨ ²log(x² - 18x + 69) = -2 x² - 18x + 69 = 2² ∨ x² - 18x + 69 = 2^-2 x² - 18x + 65 = 0 ∨ x² - 18x + 68,75 = 0 (x - 5)(x - 13) = 0 ∨ (x - 5,5)(x - 12,5) = 0 (of de ABC-formule) x = 5 ∨ x = 13 ∨ x = 5,5 ∨ x = 12,5

14.	voor de asymptoten geldt: x² - ax + 69 = 0ABC-formule: x = ^{(a + √(a²- 276))}/₂ ∨ x = ^{(a + √(a²- 276))}/₂ de afstand daartussen is √(a² - 276) √(a² - 276) = 20 a² - 276 = 400 a² = 676 a = 26

15.	e^ax = e geeft ax = 1 dus x = ¹/_a de afgeleide is f '(x) = ae^ax x = ¹/_a geeft f '(x) = ae¹ = ae de raaklijn is de lijn y = aex + b en gaat door (¹/_a, e) e = ae × ¹/_a + b b = 0 Dus de raaklijn gaat door de oorsprong.

16.	Spiegelen in y = x betekent x en y omwisselen. A(0,1) dus D(1,0) B(1, e^a) dus E(e^a, 1) C(2, e^2a) dus F(e^2a, 2) AD² = 1^2 +1² = 2 dus AD = √2 BE² = (1 - e^a)² + (e^a - 1)² = 2(e^a - 1)² dus BE = (e^a - 1)√2 CF² = (2 - e^2a)² + (e^2a - 2)² = 2(e^2a - 2)² dus CF = (e²^a - 2)√2 AD + BE = CF √2 + (e^a - 1)√2 = (e²^a - 2)√2 1 + e^a - 1 = e^2a - 2 e^2a - e^a - 2 = 0 (e^a)² - e^a - 2 = 0 (e^a - 2)(e^a + 1) = 0 e^a = 2 ∨ e^a= -1 de tweede geeft geen oplossing e^a = 2 geeft a = ln2

17.	Q(a, b) en OQ = 5Ö5 dus a² + b² = (5√5)² = 125

	¹/₂√2 × √810 × 5√5 = 9a + 27b 225 = 9a + 27b 225 = 9a + 27b a = 25 - 3b invullen in a² + b² = 125 (25 - 3b)² + b² = 125 625 - 150b + 9b² + b² = 125 10b² - 150b + 500 = 0 b² - 15b + 50 = 0 (b - 5)(b - 10) = 0 b = 5 ∨ b = 10 De coördinaten zijn dan (10, 5) en (-5, 10)

VWO WB, 2024 - II