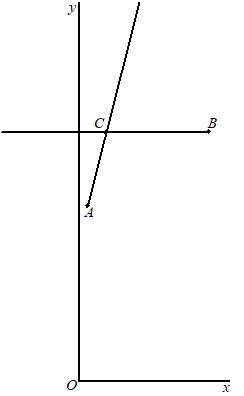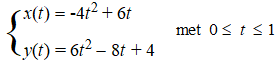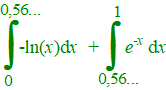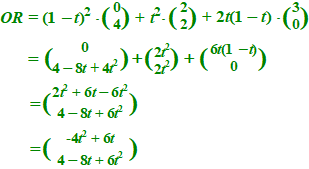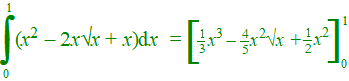Inverse van lnx
De functies fp  en gp zijn gegeven door:
De functies  fp  en gp zijn elkaars inverse.
3p.	1.	Bewijs dit.
Neem p = −1. V is het gebied dat wordt ingesloten door de grafieken van f−1 en g−1 , de x-as en de y-as. Zie de figuur hiernaast.
5p.	2.	Bereken de oppervlakte van V. Geef je eindantwoord in twee decimalen.
Er bestaat een waarde van p waarbij de lijn y = x de gemeenschappelijke raaklijn is van de grafieken van fp en gp . Deze situatie is in de figuur hiernaast weergegeven.
4p.	3.	Bereken exact de waarde van p waarvoor de lijn y = x de gemeenschappelijke raaklijn is van de grafieken van fp en gp .

Letter op het computerbeeldscherm.
De rand van een letter op een computerbeeldscherm is een aaneenschakeling van meerdere krommen. Zo is de rand van de (uitvergrote) letter ‘a’ in de figuur 1 gemaakt met behulp van zestien krommen, die je in figuur 2 ziet.
Elk van de zestien krommen kan met een formule worden beschreven. Computers hebben die formules nodig om de letters op het scherm te kunnen tekenen. Als voorbeeld bekijken we de kromme K tussen A en B, die in figuur 2 dikker is getekend. We gaan ervan uit dat er vier gegevens bekend zijn:
-	de coördinaten van A;
-	de coördinaten van B;
-	de richting van de raaklijn in A aan de kromme;
-	de richting van de raaklijn in B aan de kromme.
Zie figuur 3. De vraag is nu hoe je uit deze vier gegevens een formule voor de kromme K maakt. In figuur 4 zie je de punten A en B en de twee raaklijnen, geplaatst in een assenstelsel. Gegeven is dat A de coördinaten (1/15, 4/3), heeft, B de coördinaten (1, 19/10), dat de raaklijn in B horizontaal is en dat de richtingscoëfficiënt van de raaklijn in A gelijk is aan 4. Het punt C is het snijpunt van de twee raaklijnen en speelt een belangrijke rol bij de constructie van de kromme K.
3p.	4.	Bereken exact de x-coördinaat van C.
Om de kromme K te kunnen construeren, worden er, behalve de drie vaste punten A, B en C, drie bewegende punten P, Q en R gebruikt. Deze bewegen als volgt:
-	Punt P beweegt voor 0 ≤ t ≤ 1 met een constante snelheid over lijnstuk AC van A naar C. Er geldt: OP = OA + t  • AC
-	Punt Q beweegt voor 0 ≤ t ≤ 1 met een constante snelheid over lijnstuk CB van C naar B. Er geldt: OQ = OC + t • CB
-	Terwijl punten P en Q bewegen, schuift punt R op het bewegende lijnstuk PQ van P naar Q. Er geldt: OR = OP + t • PQ
-	Het punt R doorloopt van t = 0 tot t =1 een kromme van A naar B.
Deze kromme wordt de Bézierkromme (van A, B en C) genoemd, en dat is kromme K uit figuur 2.
3p.	5.	Teken in de figuur hiernaast het punt R van de Bézierkromme dat hoort bij t = 0,25 . Licht je werkwijze toe.
Er geldt voor elke waarde van t:
5p.	6.	Bewijs dit.
In de rest van deze opgave kijken we naar een ander voorbeeld. Het gaat niet meer om de letter ‘a’. De coördinaten van A, B en C zijn nu als volgt: A(0, 4), B(2, 2) en C(3, 0) . Ook nu is C het snijpunt van de raaklijnen in A en B. De Bézierkromme van A, B en C is, volgens de formule voor OR, te beschrijven met behulp van vectoren. Het is echter ook mogelijk deze Bézierkromme met bewegingsvergelijkingen te beschrijven.
We bekijken het punt L met de volgende bewegingsvergelijkingen:
De baan van L is weergegeven in de figuur hiernaast. Er geldt: de baan van L is de Bézierkromme die hoort bij de punten A, B en C.
3p.	7.	Bewijs dit met behulp van de formule voor OR.

Gebroken sinusfunctie.
De functie f is voor −π < x < π gegeven door:
De functie g is gegeven door g(x) = sin(x). In de figuur zijn de grafieken van f en g weergegeven.
8p.	8.	Bewijs dat de grafieken van f en g elkaar in twee punten raken.

Raaklijn verschuiven.
De functie f is gegeven door  f(x) = x2 - 2x√x + x  met x ≥ 0 . In de figuur is de grafiek van f met haar raaklijn k in de oorsprong weergegeven. De grafiek van f heeft de punten (0, 0) en (1, 0) gemeenschappelijk met de x-as.
4p.	9.	Bewijs dat er geen andere gemeenschappelijke punten van de grafiek van f met de x-as zijn.
4p.	10.	Bereken exact de oppervlakte van het vlakdeel ingesloten door de grafiek van f en de x-as.
Er is een waarde van a, met a ≠ 0, waarbij een verschuiving van de raaklijn k
weer een raaklijn aan de grafiek van f geeft.
7p.	11.	Bereken exact deze waarde van a.

Vulkaan.
Een vulkaan kan op verschillende manieren tot uitbarsting komen. Bij een zogenoemde plinische uitbarsting wordt de druk binnen de vulkaan steeds groter totdat de vulkaan met groot geweld tot uitbarsting komt. Bij de uitbarsting worden brokken gesmolten steen weggeslingerd die lavabommen worden genoemd.
In een model van de baan van een lavabom wordt ervan uitgegaan dat op het moment van de uitbarsting alle lavabommen een snelheid hebben van 210 meter per seconde. Een tweede uitgangspunt is dat elke lavabom een parabolische baan beschrijft. De hoogte van de vulkaan ten opzichte van de grond is 2000 meter. In onderstaande figuur zie je de banen van een aantal lavabommen die in het vlak door de x-as en de y-as bewegen.
De bewegingsvergelijkingen van een lavabom hangen af van de richting waarin de lavabom tijdens de uitbarsting wordt weggeslingerd. In het model worden de volgende bewegingsvergelijkingen als uitgangspunt genomen:
		x(t) = 210 cos(α) • t y(t) = 2000 + 210sin(α) • t  - 4,9t2
Hierbij is α de hoek die de baan van de lavabom op het moment van wegslingeren maakt met een horizontale lijn, waarbij 0 < α < π. Verder is t de tijd in seconden (waarbij t = 0 het moment van wegslingeren is) en zijn x(t) en y(t) in meters. Uitgaande van dit stelsel kan de y-coördinaat van de baan worden uitgedrukt in x en α . Er geldt (voor α ≠ 1/2π ):
3p.	12.	Bewijs dit.
Een lavabom wordt onder een hoek α =1 (radiaal) weggeslingerd. Deze lavabom komt op een bepaalde afstand van de vulkaan op de grond. Voor dit punt geldt y = 0 .
3p.	13.	Bereken deze afstand. Geef je eindantwoord in honderden meters nauwkeurig.
De formule voor y kan worden herleid tot:
In onderstaande figuur is bij de parabolische banen van een aantal lavabommen een gestippelde kromme getekend. Deze kromme stelt de uiterste grens voor van het gebied dat door deze lavabommen kan worden bereikt.
De formule van de gestippelde kromme is
Alle banen van de lavabommen hebben precies één punt gemeenschappelijk met de gestippelde kromme en raken dus aan deze kromme.
4p.	14.	Bewijs dat alle banen van de lavabommen raken aan de gestippelde kromme.

Scheve asymptoot.
De functie f  is gegeven door f (x) = x + 2/x. De grafiek van f  heeft een verticale asymptoot met vergelijking x = 0 en een scheve asymptoot. In de figuur hiernaast is voor x > 0 de grafiek van f weergegeven. De scheve asymptoot is gestippeld weergegeven. Op de grafiek van f  ligt een willekeurig punt P (p, p + 2/p). De raaklijn aan de grafiek van f  in P snijdt de verticale asymptoot in punt Q en de scheve asymptoot in punt R. Zie de figuur.
8p.	15.	Bewijs dat P het midden is van lijnstuk QR.

Vlieger.
Gegeven zijn voor a > 0 de punten A(0, a), B(1, 0), C(0, 1) en D( 1, 0). Vierhoek ABCD is een vlieger. In de figuur hiernaast is de vlieger getekend voor a = 2. De middelloodlijn van een lijnstuk gaat door het midden van dat lijnstuk en staat loodrecht op dat lijnstuk. Voor a = 2 gaat de middelloodlijn van lijnstuk AB niet door D.
5p.	16.	Bereken exact voor welke waarde van a de middelloodlijn van lijnstuk AB wél door D gaat.
In de hoekpunten van de vlieger bevinden zich puntmassa’s:
-	in punt A met gewicht 2;
-	in zowel B als D met gewicht 1;
-	in punt C met gewicht a.
In de linker figuur hieronder  zijn de vlieger, de puntmassa’s en het zwaartepunt Z van de puntmassa’s getekend voor het geval a =1. In de rechterfiguur hieronder  zijn de vlieger, de puntmassa’s en het zwaartepunt Z getekend voor het geval a = 2. Wanneer a groter wordt, verschuift het punt A(0, a) over de y-as omhoog en neemt het gewicht in C toe. Ook het zwaartepunt Z van de vier puntmassa’s verandert dan van plaats. Wanneer a onbegrensd toeneemt, nadert het zwaartepunt Z tot een vast punt P.
4p.	17.	Bewijs dat de y-coördinaat van dat punt P gelijk is aan 1.

UITWERKING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1.	y = pln(x) De inverse is  x = pln(y) x/p = ln(y) y = ex/p
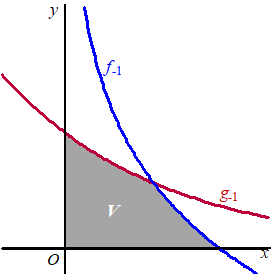
2.	Het mag allemaal met de GR. Snijpunt: Y1 = e-x Y2 = -ln(x) intersect  x = 0,5671433...
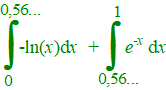	= 0,432... + 0,111... = 0,54
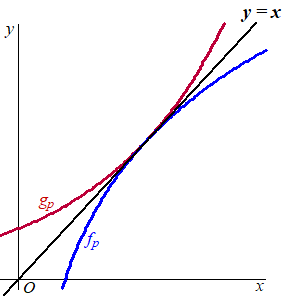
3.	de hellingen moeten 1 zijn en de functies moeten gelijk zijn. f ' = p/x = 1   ofwel  p = x g' = 1/p • ex/p = 1 vul  p = x in deze laatste in:  1/x • e1 = 1  ofwel  x = e  is het raakpunt Dus p = x = e
4.	raaklijn in A :  door (1/15, 4/3) met r.c. 4 is de lijn  y = 4x + 16/15 raaklijn in B:   door (1, 19/10) met r.c.  0  is de lijn  y = 19/10 snijden geeft  19/10 = 4x + 16/15 4x = 5/6 x = 5/24
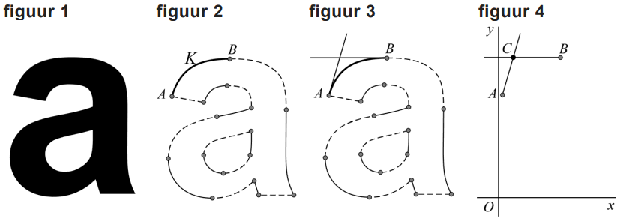
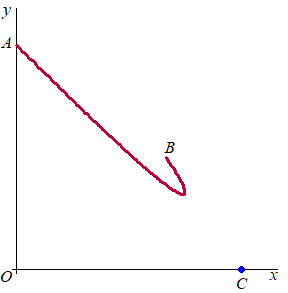
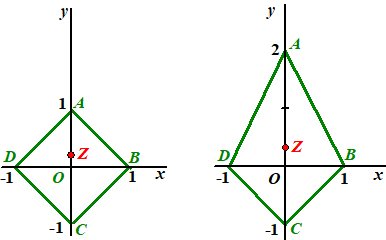
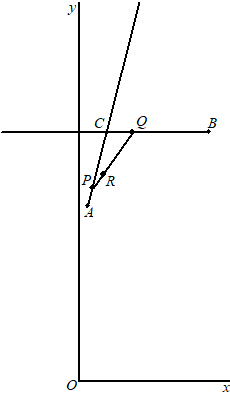
5.	Omdat de punten P, Q en R met constante snelheid bewegen hebben ze op t = 0,25 precies een kwart van de totale afstand afgelegd. Hiernaast is dus AP = 1/4 • AC CQ = 1/4 • CB PR = 1/4 • PQ
6.	OR = OP + t • PQ OP = OA + t • AC = OA + t(OC - OA) Dus  OR = OA + t(OC - OA) + t • PQ     ....(1) OQ = OC + CQ = OC + t • CB = OC + t • (OB - OC) PQ = OQ - OP = OC + t • (OB - OC) - OA - t • (OC - OA) dan geeft (1):   OR = OA + t • (OC - OA) + t •(OC +  t • (OB - OC) - OA - t • (OC - OA)) haakjes wegwerken: OR = OA + t • OC - t • OA + t • OC +  t2 • OB - t2 • OC - t • OA - t2 • OC + t2 •OA OR = OA • (1 - t - t + t2) + OB • (t2) + OC • (t + t - t2 - t2) OR = OA • (1 - 2t + t2) +  OB • t2 + OC • (2t - 2t2) OR = OA • (1 - t)2 + OB • t2 + OC • 2t(1 - t)
7.
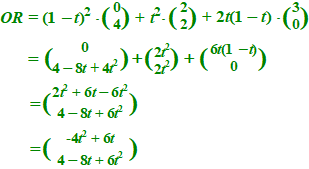8.	Snijpunten: sin(x) = sin(x)/sin(2x)  sin(x) • sin(2x) = sin(x)    (en sin(2x) ≠ 0) sin(x)sin(2x) - sin(x) = 0 sin(x) • (sin(2x) - 1) = 0 sin(x) = 0  ∨ sin(2x) = 1 x = 0  ∨  2x = 1/2π  +  k2π x = 0  ∨ x = 1/4π  ∨  x = -3/4π De snijpunten zijn  x = 1/4π  en  x = -3/4π Als de grafieken raken moeten de hellingen daar ook gelijk zijn. f '(x) =  (cos(x)sin(2x) - sinx•2cos(2x))/sin²2x   en   g '(x) = cos(x) x = 1/4π  geeft  f ' = (0,5√2 - 0)/(1) = 1/2√2     en  g ' = 1/2√2 x = -3/4π  geeft  f ' =  (-0,5√2 - 0)/(1) = -1/2√2      en  g ' =  -1/2√2
9.	x2 - 2x√x + x  = 0 x(x - 2√x + 1) = 0 x = 0  ∨  (√x - 1)2 = 0 x = 0  ∨ √x = 1 x = 0  ∨ x = 1
10.
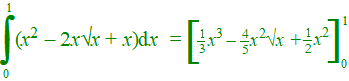	=  (1/3 - 4/5 + 1/2) - (0) = 1/30
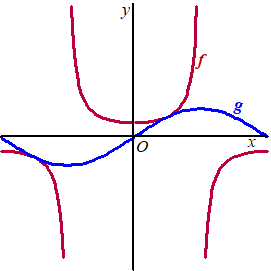
11.	f(x) = x2 - 2x√x + x f '(x) = 2x - 3√x + 1 f '(0 ) = 1 f '(x) = 1 geeft  2x -3√x + 1 = 1 2x - 3√x = 0 √x(2√x - 3) = 0 √x = 0   ∨  √x = 3/2 x = 0 ∨ x = 9/4  x = 9/4   geeft  y =  81/16 - 2• 9/4 •  3/2 +  9/4  =  9/16 De raaklijn bij  x = 9/4   is  y = x + b  dus  9/16 = 9/4 + b   dus  b = -27/16 De raaklijn is  y = x - 27/16  en die snijdt de x-as in (27/16, 0) Dat was de oorsprong dus de lijn is 27/16 naar rechts geschoven. Dus  a = 27/16
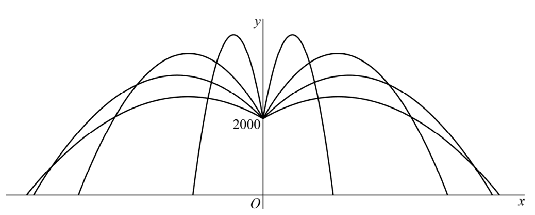
12.	x(t) = 210cos(α)•t  geeft  t = x/210cos(α) Dat kun je invullen in de tweede vergelijking: y = 2000 + 210sin(α) • t  - 4,9t2     =  2000 + 210sin(α) •  x/210cos(α)  - 4,9 ( x/210cos(α))2    =  2000 + 210x • sin(α)/cos(α) - 4,9x²/(44100cos²(α))     =  2000 + 210x • tan(α) - x2 • 1/(9000cos²(α))
13.	y =  2000 + 210x • tan(1) - x2 • 1/(9000cos²(1)) Invoeren in de GR en dan intersect geeft  x = 5100 of  x = -1000 Het tweede antwoord voldoet niet, dus x = 5100 m
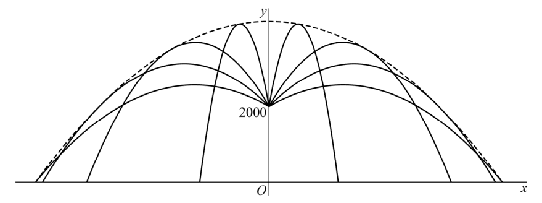
14.	Snijden van de y-krommen met deze gemeenschappelijke kromme geeft: -1/9000 • x2 + 4250 = -(1 + tan²(α))/9000 • x2 + tan(α)•x + 2000 Dat is een kwadratische formule voor x. {-1/9000 + (1 + tan²(α))/9000 } • x2  - {tan(α)}• x   + 2250 = 0 tan²(α)/9000 • x2 - tan(α)• x   + 2250 = 0 De grafieken raken elkaar als deze vergelijking één oplossing heeft. Dat is zo als D = 0 D = tan2(α) - 4 • tan²(α)/9000 • 2250 D = tan2(α) - tan2(α) = 0 q.e.d.
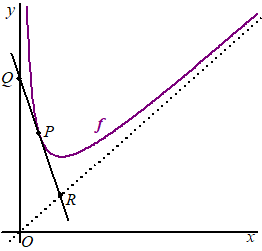
15.	raaklijn in P f '(x) = 1 - 2x-2 f '(p) = 1 - 2/p² De raaklijn is  y = (1 - 2/p²)x + b en gaat door  (p, p + 2/p) Dat geeft  p + 2/p  =  (1 - 2/p²) • p + b p + 2/p =  p - 2/p + b b = 4/p De raaklijn is  y =  (1 - 2/p²)x + 4/p  De verticale asymptoot is x = 0  dus dat geeft  Q = (0,  4/p) De scheve asymptoot is  y = x   (voor grote x kun je 2/x verwaarlozen) (1 - 2/p²)x + 4/p   = x 4/p =  2/p²  • x  x = 2p  dus  R =  (2p, 2p) Het midden van QR is    (0,5(0 + 2p),  0,5(4/p + 2p)) = (p,  2/p + p) Dat is inderdaad punt P
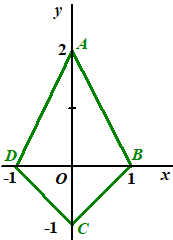
16.	A = (0, a) en  B = (1, 0) Het midden van AB is  M = (0.5, 0.5a) AB  heeft r.c. -a/1 = -a De middelloodlijn staat daar loodrecht op dus heet r.c. 1/a De middelloodlijn is de lijn  y = 1/a • x + b  en gaat door  (0.5, 0.5a) Dat geeft  0.5a = 1/a • 0.5 + b  dus  b = 0,5a - 0.5/a D is het punt  (-1, 0) Als dat op de middelloodlijn ligt dan moet gelden:  0 = 1/a • -1 + 0.5a - 0,5/a Vermenigvuldig alles met a:   0 = -1 + 0,5a2 - 0,5 0,5a2 = 1,5 a2 = 3 a = √3
17.	Het zwaartepunt ligt (vanwege de symmetrie) op de y-as. De gemiddelde y-coördinaat van de punten A(0, a) met weging 2  en  C(-1, 0) met weging a  is gelijk aan  -1 • a + a • 2 = a Het totale gewicht is 4 + a  dus yZ =  a/(4 + a)
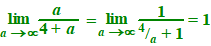