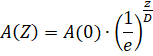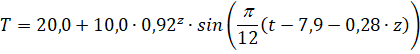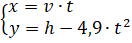Nieuwe pagina 1

Twee functies.

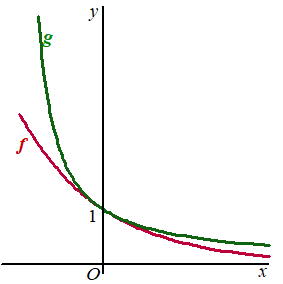
De functies f en g zijn gegeven door: f(x) = e^-x en g(x) = ¹/_{(x + 1)} met x > -1 In figuur hiernaast zijn de grafieken van f en g getekend. Beide grafieken gaan door het punt (0, 1) en de twee grafieken hebben in (0, 1) dezelfde helling. Behalve x = 0 is er nog een tweede waarde van x waarvoor de grafieken van f en g dezelfde helling hebben.

4p.	1.	Bereken deze waarde van x in twee decimalen nauwkeurig.

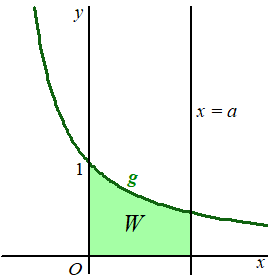
Het vlakdeel ingesloten door de grafiek van g, de y-as, de x-as en de lijn x = a , met a > 0 , noemen we W. Zie onderstaande figuur.



Als de waarde van a onbegrensd toeneemt, neemt de oppervlakte van W ook onbegrensd toe. Er is bijvoorbeeld een waarde van a waarvoor geldt: de oppervlakte van W is 2011.

4p.	2.	Bereken exact deze waarde van a.

Temperatuur in de aardbodem.

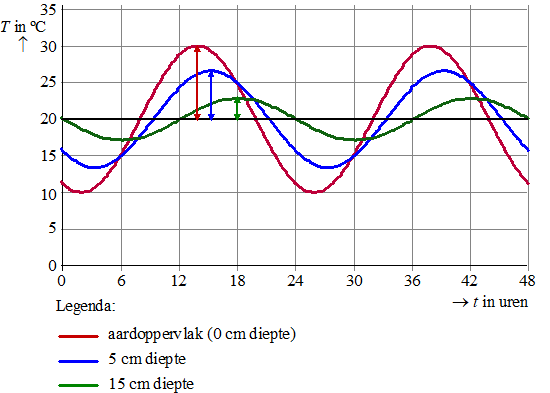
Per 24 uur schommelt de temperatuur aan het aardoppervlak en daardoor ook de temperatuur in de aarde. Naarmate je op een bepaalde plek dieper de aardbodem ingaat, zijn de temperatuurschommelingen minder groot. Bovendien lopen ze achter in de tijd ten opzichte van de temperatuurschommeling aan het aardoppervlak. In onderstaande figuur zie je voor een bepaalde plaats in Nederland het dagelijkse temperatuurverloop op verschillende dieptes als functie van de tijd t, met t in uren. Hierbij geldt t = 0 om middernacht in het begin van een week met zacht zomerweer. Voor elk van deze geringe dieptes is de evenwichtsstand van het temperatuurverloop (bij benadering) 20,0 ºC. Bij elke grafiek is met een dubbele pijl de amplitude aangegeven.



De amplitude van het temperatuurverloop blijkt exponentieel af te hangen van de diepte in de aardbodem. De diepte waarop de amplitude is afgenomen tot ¹/_e-de deel van de amplitude aan het aardoppervlak wordt de dempingsdiepte genoemd. Er geldt:


Hierin is z de diepte in de aardbodem in centimeter, A(z) de amplitude van het temperatuurverloop in graden Celsius op diepte z cm en D de dempingsdiepte in centimeter. In de figuur zijn onder andere de amplitudes A(0) =10,0 en A(15) = 2,9 aangegeven.

3p.	3.	Bereken uitgaande van de genoemde amplitudes de waarde van D in één decimaal nauwkeurig.

Gebruikmakend van de waarden van A(0) en D kan de formule voor de amplitude worden herschreven tot A(z) =10,0 • 0,92^z. Met deze formule werken we in het vervolg van deze opgave. De grafieken in de figuur zijn sinusoïden met een evenwichtsstand van 20,0 ºC en een periode van 24 uur. De grafiek die hoort bij z = 0 gaat bij t = 7,9 stijgend door de evenwichtsstand. Bij elke centimeter dieper in de aardbodem gaat de bijbehorende grafiek ongeveer 0,28 uur later door de evenwichtsstand. Voor de situatie van de figuur komen we uit op de volgende formule voor de temperatuur in de aardbodem:



Hierin is z de diepte in de aardbodem in centimeter, T de temperatuur op deze diepte in graden Celsius en t de tijd in uren met t = 0 om middernacht. Deze formule geldt voor 0 ≤ z ≤ 30 en 0 ≤ t ≤ 48 . De temperatuur op 15 cm diepte in de aardbodem bereikt op een bepaald tijdstip van de dag zijn maximale waarde.

6p.	4.	Bereken dit tijdstip op algebraïsche wijze.

Koorde evenwijdig aan raaklijn.

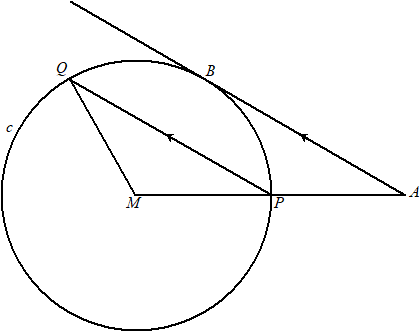
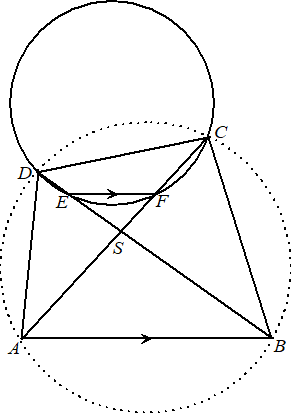
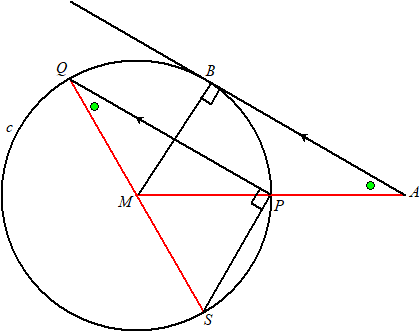
Gegeven is een cirkel c met middelpunt M en een punt P op c. Op het verlengde van de straal MP ligt het punt A zo dat MP = PA. Een raaklijn door A aan c raakt de cirkel in het punt B. Het punt Q ligt op c zo dat de koorde PQ evenwijdig is aan de raaklijn AB. Zie onderstaande figuur. In deze figuur is ook de straal MQ getekend.



Er geldt: ∠MQP = ∠BAM

3p.	5.	Bewijs dit. Je kunt hierbij gebruik maken van de figuur.

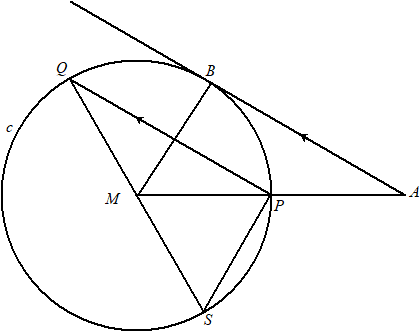
Het verlengde van QM snijdt de cirkel c in het punt S. Zie onderstaande figuur. In deze figuur zijn ook de straal MB en de koorde PS getekend.



5p.	6.	Bewijs dat PS = MB . Je kunt hierbij gebruik maken van de figuur

Wortelfunctie met cosinus.

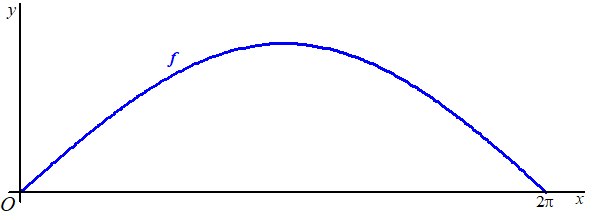
In de volgende figuur is een sinusoïde getekend die de grafiek is van een functie f met domein [0,2π] .



Het bijbehorende functievoorschrift kan op dit domein geschreven worden als f (x) = √(1 - cos x)

5p.	7.	Bereken exact de richtingscoëfficiënt van de raaklijn aan de grafiek van f in het punt op de grafiek waarvan de y-coördinaat ¹/₂√6 is en de x-coördinaat groter dan π is.

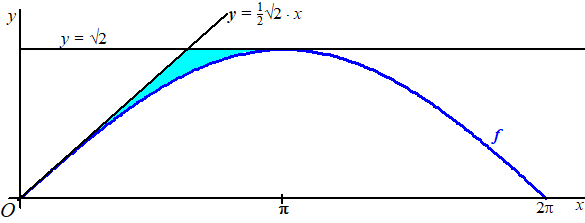
In onderstaande figuur zijn de grafiek van f en de lijnen y = ¹/₂√2 • x en y = √2 getekend. Deze lijnen raken de grafiek van f in respectievelijk (0, 0) en (π, 2). Het vlakdeel V wordt begrensd door de grafiek van f en de twee genoemde lijnen. Dit vlakdeel is in de figuur blauw gemaakt.



Het omwentelingslichaam L ontstaat bij wenteling van V om de x-as.

8p.	8.	Bereken exact de inhoud van L. Schrijf je antwoord zo eenvoudig mogelijk.

Twee lijnen die raken aan parabolen.

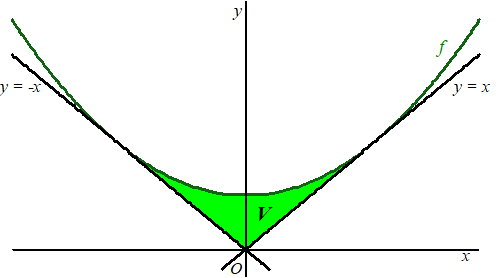
De functie f is gegeven door f(x) = 3x² + ¹/₁₂. De lijn met vergelijking y = x raakt aan de grafiek van f. Vanwege symmetrie in de y-as raakt ook de lijn y = -x aan de grafiek van f. Het vlakdeel V wordt begrensd door de grafiek van f en de twee raaklijnen. Zie de figuur.



6p.	9.	Bereken exact de oppervlakte van het vlakdeel V.

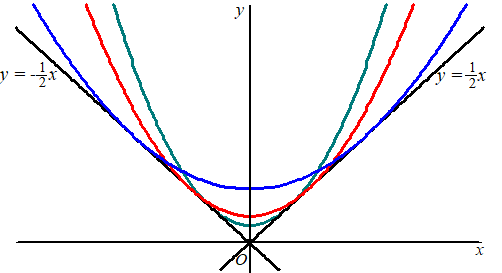
Voor elk tweetal positieve waarden van a en b is de functie g_a_,_b gegeven g_a_,_b (x) = ax² + b . We bekijken de functies g_a_,_b die de lijn y = ¹/₂x (en dus ook de lijn y = -¹/₂x) als raaklijn aan hun grafiek hebben. In onderstaande figuur zijn de grafieken van drie van zulke functies en de lijnen y = ¹/₂x en y = -¹/₂x getekend



Voor alle functies g_a_,_b die de lijn y = ¹/₂x (en dus ook de lijn y = -¹/₂x) als raaklijn aan hun grafiek hebben, kunnen we b uitdrukken in a.

6p.	10.	Druk voor deze functies b uit in a. Schrijf je antwoord zo eenvoudig mogelijk.

Koordenvierhoek en gelijke hoeken.

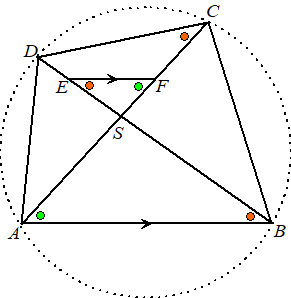
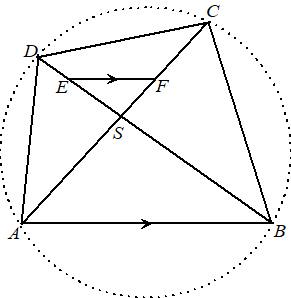
Gegeven is koordenvierhoek ABCD met de twee diagonalen AC en BD, die elkaar in punt S snijden. Op lijnstuk CS ligt punt F en op lijnstuk DS ligt punt E zó dat de lijnstukken AB en EF evenwijdig zijn. Zie de figuur hiernaast. De cirkel door de hoekpunten van de koordenvierhoek is in deze figuur gestippeld. Vierhoek CDEF is een koordenvierhoek.

5p.	11.	Bewijs dit.

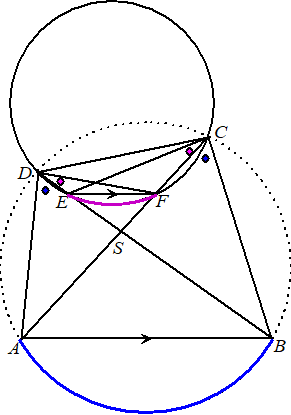
In onderstaande figuur is, behalve de situatie van de vorige figuur, ook de cirkel door de punten C, D, E en F getekend.



3p.	12.	Bewijs dat ∠ADF = ∠BCE.

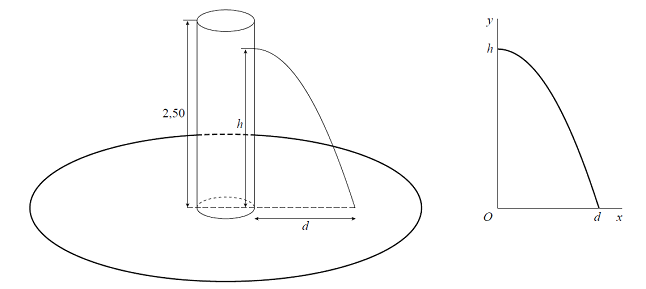
Fontein.

Op de foto is de Crown Fountain in Chicago te zien. In onderstaande figuur is een cilindervormige vijverfontein getekend die volgens hetzelfde principe werkt. In de verticale, holle cilinderbuis wordt water tot een hoogte van 2,50 meter opgepompt. In de buis is op een hoogte h meter boven de grond een klein gat aangebracht. Uit dit gat spuit in horizontale richting water. Omdat de pomp er ondertussen voor zorgt dat het water in de buis 2,50 meter hoog blijft, krijgen we een waterstraal te zien die bij benadering de vorm heeft van een halve parabool. De waterstraal komt op afstand d meter van de cilinderbuis op het wateroppervlak in de vijver. Zie de figuren hieronder.



De horizontale uitstroomsnelheid v van het water bij het gat hangt af van de hoeveelheid water die zich boven het gat bevindt en dus van de hoogte h van het gat. Er geldt bij benadering:



met v in meter per seconde en h in meter. In een geschikt assenstelsel beweegt een waterdruppel (uit de waterstraal) met coördinaten (x, y) bij benadering volgens de vergelijkingen:


Hierin is t de tijd in seconden en t = 0 op het moment dat de waterdruppel het gat passeert (zodat dan geldt x = 0 en y = h). Voor de waarde van t die hoort bij het tijdstip waarop de waterdruppel in de vijver valt, geldt x = d en y = 0 . Zie de figuren hierboven.


5p.	13.	Leid langs algebraïsche weg deze laatste formule af uit de gegeven formules voor v, x en y.

Door de hoogte h van het gat te veranderen, verandert ook de plaats waar de waterstraal in de vijver terechtkomt. Er is een hoogte van het gat waarvoor de afstand van deze plaats tot de buis maximaal is.

4p.	14.	Bereken langs algebraïsche weg deze maximale afstand. Rond je eindantwoord af op hele centimeters.

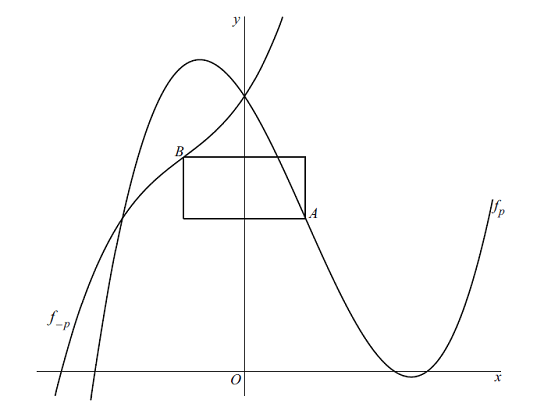
Vierkant tussen buigpunten.

De functie f_p is voor elke waarde van p gegeven door: f_p(x) = (x - 3p) • (x² - 3p) Voor elke waarde van p hebben de grafieken van f_p en f_-p beide een buigpunt. In de onderstaande figuur zijn voor een waarde van p met p > 0 de grafieken van f_p en f_-_p met hun buigpunten A en B getekend. Verder is de rechthoek met hoekpunten A en B getekend waarvan twee zijden evenwijdig zijn met de x-as en de andere twee zijden evenwijdig zijn met de y-as.



De coördinaten van de buigpunten zijn afhankelijk van p. Er is een positieve waarde van p waarvoor de rechthoek een vierkant is.

9p.	15.	Bereken deze waarde van p. Geef je antwoord in twee decimalen nauwkeurig.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.	f(x) = e^-x geeft f '(x) = -e^-xg(x) = 1/(x + 1) geeft g '(x) =^-1/_{(x + 1)}2Y1 = -e^(-X) Y2 = -1/(X+1)^2 inetersect geeft X = 2,51.

2.
	ln(a + 1) = 2011 a + 1 = e²⁰¹¹ a = e²⁰¹¹ - 1

3.	De gegevens invullen: 2,9 = 10,0 • (1/e)^15/D 2,9 = 10,0 • e^-15/D0,29 = e^-15/D-¹⁵/_D = ln(0,29)D = ^-15/_ln0,29 = 12,1

4.	20,0 + 10,0 • 0,92¹⁵ • sin(^π/₁₂(t - 7,9 - 0,28 • 15) moet maximaal zijn. Dat is maximaal als de sinus gelijk is aan 1: sin(^π/₁₂(t - 12,1)) = 1 ^π/₁₂(t - 12,1) = ¹/₂π + k2π t - 12,1 = 6 + k • 24 t = 18,1 + k • 24 Dat is om 18:06 uur.

5.	∠MQP = ∠MPQ (gelijkbenige driehoek, want twee zijden zijn gelijk aan de straal van de cirkel. ∠MPQ = ∠MAB (Z- hoeken) dus ∠MQP = ∠MAB. qed

6.	∠MAB = ∠MQP (vorige vraag) MA = QS (middellijn is tweemaal straal) ∠MBA = ∠QPS = 90º (raaklijn en thales) Dus de driehoeken SQP en MBA zijn gelijkvormig (HHZ) Dus BM = PS

7.	√(1 - cos x) = ¹/₂√6 1 - cosx = ¹/₄ • 6 = 1,5 cosx = -0,5 x = ²/₃π + k2π ∨ x = - ⁴/₃ππ + k2π De x-coördinaat groter dan π is x = ⁴/₃π f '(x) = ¹/₂ • (1 - cosx)^-1/2 • sinx ⁴/₃π invullen: f ' = ¹/₂ • (1 - -¹/₂)^-1/2 • -¹/₂√3 = ¹/₂ • ¹/₍_√_3/2) • -¹/₂√3 = -¹/₄ • ^√²/_√₃ • √3 = -¹/₄√2

8.	¹/₂√2 • x = √2 x = 2 wentel eerste beide rechte lijnen om de x-as: schuine stuk geeft een kegel; met inhoud ¹/₃ • π • (√2)² • 2 = ⁴/₃π horizontale deel geeft een cilinder met inhoud π • (√2)² • (π - 2) = 2π² - 4π wentel nu de grafiek om de x-as:

	De gevraagde inhoud is dan ⁴/₃π + 2π² - 4π - π² = π² - 2²/₃π

9.	Bereken de rechterhelft. Raakpunt: 3x² + ¹/₁₂= x en 6x = 1 Dat geeft x = ¹/₆

	= (¹/₆)³ + ¹/₆ • ¹/₁₂ - ¹/₂ • (¹/₆)² - 0 = ¹/₂₁₆ De hele oppervlakte is dan ²/₂₁₆ = ¹/₁₀₈

10.	ax² + b .= ¹/₂x en 2ax = ¹/₂ De tweede vergelijking geeft x = ¹/_4a en dat kun je invullen in de eerste: a • (¹/_4a)² + b = ¹/₂ • ¹/₄_a ¹/_16a + b = ¹/₈_a b = ¹/_8a - ¹/_16a = ²/_16a -¹/_16a = ¹/₁₆_a Dus b = ¹/₁₆_a

11.	∠FES = ∠ABD (Z-hoeken) ∠ACD = ∠ABD (omtrekshoek van koorde AD) Dus ∠FES = ∠ACD ∠FED = 180 - ∠FES (gestrekte hoek) Dus ∠FED + ∠ACD = 180º Dus is CDEF een koordenvierhoek.

12.	De blauwe koorde AB geeft gelijke blauwe hoeken ADB en ACB De paarse koorde EF geeft gelijk paarse hoeken FDE en FCE de hoeken BCE en ADF zijn beiden gelijk aan een blauwe plus een paarse hoek, dus ze zijn even groot.

13.	y = 0 geeft h - 4,9t² = 0 2,9t² = h t² = h/4,9 t = √(^h/_4,9) d = x = v • t = √(19,6(2,50 - h) • √(^h/_4,9) d = √(19,6(2,50 - h) •^h/_4,9) d = √(4h(2,50 - h)) d = √4 • √(h(2,50 - h)) d = 2√(h(2,50 - h))

14.	d = 2√(h(2,50 - h)) en dat is maximaal als dat deel onder die wortel maximaal is. h(2,50 - h) = 2,50h - h² moet maximaal zijn dan is de afgeleide nul: 2,50 - 2h = 0 geeft h = 1,25 Dan is d = 2√(1,25 • (2,50 - 1,25)) = 2,50 meter.

15.	f_p(x) = (x - 3p) • (x² - 3p) = x³ - 3px - 3px² + 9p² f ' = 3x² - 3p - 6px f '' = 6x - 6p = 0 Dat is zo bij x = p het buigpunt van f_p heeft x = p en y = (p - 3p) • (p² - 3p) = -2p • (p² - 3p) = -2p³ + 6p² het buigpunt van f_-p heeft x = -p geeft dan y = -2(-p)³ + 6 • (-p)² = 2p³ + 6p² de afstand tussen de beide x-waarden is een zijde van de rechthoek en is 2p de afstand tussen beide y-waarden is een zijde van de rechthoek en is 4p³ voor een vierkant moet dan gelden 2p = 4p³ 4p³ - 2p = 0 2p(2p² - 1) = 0 p = 0 ∨ 2p² = 1 p = 0 ∨ p = √(¹/₂) = ¹/₂√2 p = 1¹/₂√2 ≈ 0,71

VWO WB, 2018 - II Bezem.