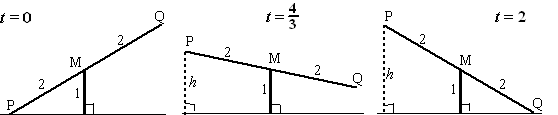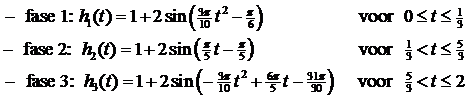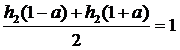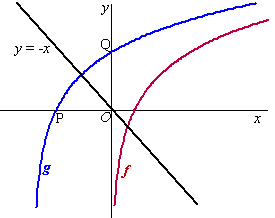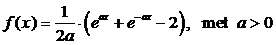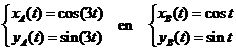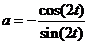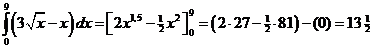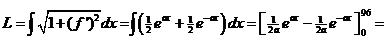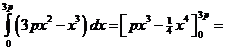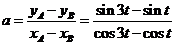Gelijke oppervlakte.
Voor x ≥ 0 is de functie f gegeven door f (x) = 3√x - x De punten O(0, 0) en A(9, 0) liggen op de grafiek van f. Het punt T is het hoogste punt van deze grafiek. Zie de volgende figuur.
De coördinaten van T zijn (21/4, 21/4)
4p.	1.	Bewijs dat de coördinaten van T inderdaad (21/4, 21/4) zijn.
V is het vlakdeel dat wordt begrensd door de grafiek van f en de x-as. In de figuur hieronder is V grijs gemaakt.
De lijn door A en T snijdt de y-as in het punt B. In onderstaande figuur is driehoek OAB grijs gemaakt.
De oppervlakte van V en de oppervlakte van driehoek OAB zijn gelijk.
6p.	2.	Bewijs dit.

Het uiteinde van een wip.         We bekijken in deze opgave een wiskundig model voor de beweging van het uiteinde van een wip. Lijnstuk PQ met midden M en lengte 4 draait om M. De hoogte van M is 1. Zie de figuur hieronder. We kijken naar het verloop van de hoogte h van P. Op tijdstip t = 0 is de hoogte van P gelijk aan 0. Van t = 0 tot t = 2 beweegt P omhoog. In de figuur is het lijnstuk getekend op drie tijdstippen: op t = 0 , op  t = 4/3 en op t = 2.                 De hoogte van P tijdens de omhooggaande beweging wordt beschreven door het volgende model:                 Hierin zijn h1 , h2 en h3 de hoogtes van P in de verschillende fasen. In de volgende figuur is de grafiek van de hoogte van P in de fasen 1, 2 en 3 getekend.                 De hoogte van P aan het eind van fase 2 is  h2(5/3). Door t = 5/3 in te vullen in de formule van h3 kan worden bewezen dat de hoogte van P aan het begin van fase 3 gelijk is aan de hoogte van P aan het eind van fase 2.         3p. 3. Bewijs dat deze hoogtes gelijk zijn.         De helling van de grafiek van h2 aan het begin van fase 2 is  2π/5 • cos(2π/15).         4p. 4. Bewijs dat de helling van de grafiek van h1 aan het eind van fase 1 hieraan gelijk is.         Voor elke waarde van a, met 0 < a < 2/3, geldt:         4p. 5. Bewijs deze gelijkheid.

Cirkel en lijnstuk.
Gegeven zijn een cirkel c met middelpunt M en een lijnstuk AB buiten c. De lijn door A en B snijdt c niet. Lijnstuk AM snijdt c in punt C en lijnstuk BM snijdt c in punt D. De bissectrice van hoek BAM en de bissectrice van hoek ABM snijden elkaar in punt E. Zie de figuur.
5p.	6.	Bewijs dat de lijnstukken CE en DE even lang zijn.

Gespiegelde punten.
Voor x > 0 is de functie f gegeven door f(x) = 2 • ln x. De grafiek van g ontstaat door de grafiek van f over een afstand a naar links te verschuiven, waarbij a >1. De grafiek van g snijdt de x-as in punt P en de y-as in punt Q. Er is een waarde van a waarvoor het beeld van P bij spiegeling in de lijn  y = -x samenvalt met Q. Er geldt dan:  yQ = -xP . Zie de figuur.
7p.	7.	Bereken deze waarde van a. Rond je antwoord af op twee decimalen.

Ankerketting.
Een schip ligt op zee voor anker. Door stroming en wind trekt het schip aan de ankerketting. Hierdoor en door het eigen gewicht van de ankerketting neemt de ketting een vorm aan die bekend staat als een kettinglijn. In de figuur is deze situatie schematisch in een assenstelsel weergegeven. De x-as valt samen met de horizontale zeebodem, waarop het anker ligt. De oorsprong O van het assenstelsel is gekozen in het punt waar de ankerketting aan het anker is bevestigd. Aan het schip zit de ankerketting vast in punt A. We gaan ervan uit dat de ankerketting daar direct het water in gaat. Het punt A bevindt zich 96 meter rechts van de y-as.
Een kettinglijn waarvan het laagste punt door O gaat, kan worden beschouwd als een deel van de grafiek van de functie f gegeven door:
Voor de functie f geldt:
6p.	8.	Bewijs deze gelijkheid.
Voor de ankerketting in de figuur geldt a = 1/140 en 0 ≤ x ≤ 96. Hierin zijn x en f(x) in meters. Door golven en wind kan een schip flinke bewegingen maken. Bij een korte ankerketting kan dan het anker losraken. Om dit te voorkomen geeft men bij het uitwerpen van een anker de ankerketting veel lengte. Hiervoor hanteert men in de scheepvaart de vuistregel dat de lengte van de ankerketting tussen anker en schip ten minste driemaal de waterdiepte moet zijn.
5p.	9.	Onderzoek of de ankerketting in de figuur aan deze vuistregel voldoet.

Acht keer zo groot.
Voor p > 0 is de functie fp gegeven door fp(x) = 3px2 - x3 De grafiek van fp raakt de x-as in het punt O(0, 0) en snijdt deze in het punt A(3p, 0) . Verder heeft de grafiek van fp een buigpunt B(p, 2p3).
V is het gebied dat wordt ingesloten door de grafiek van fp en de x-as. De verticale lijn door het buigpunt verdeelt V in twee delen. In de figuur hiernaast  is deze situatie weergegeven. De oppervlakte van het linkerdeel is 3/4p4.
5p.	10.	Bewijs dat de oppervlakte van het rechterdeel acht keer zo groot is als de oppervlakte van het linkerdeel.
Er is een waarde van p waarvoor geldt: de lijnstukken BO en AO zijn even lang.
4p.	11.	Bereken exact deze waarde van p.
De buigraaklijn in B snijdt de x-as in punt C. In de figuur hiernaast is deze situatie weergegeven.
5p.	12.	Bewijs dat de lengte van CA voor elke waarde van p > 0 acht keer zo groot is als de lengte van OC.

Tussen twee bewegende punten.
Over de eenheidscirkel bewegen twee punten A en B. Beide punten bevinden zich op tijdstip t = 0 in het punt (1, 0). Ze bewegen met constante snelheid, waarbij de snelheid van A drie keer zo groot is als de snelheid van B. De bewegingsvergelijkingen van A en B zijn respectievelijk:
Voor t  ≠ k • π , met k geheel, vallen de punten A en B niet samen en zijn ze de eindpunten van de koorde AB . In de figuur is de situatie getekend voor t = 1/5π
Lijnstuk A'B' is de loodrechte projectie van koorde AB op de x-as. De lengte van A'B' verandert voortdurend tijdens de beweging.
4p.	13.	Bereken de maximale lengte van A'B'. Rond je antwoord af op twee decimalen.
Tijdens de beweging verandert ook de richtingscoëfficiënt van koorde AB. Deze richtingscoëfficiënt noemen we a. Voor elk tijdstip t, waarbij t ≠ k • 1/2π  met k geheel, geldt:
4p.	14.	Bewijs dit.
Lijn l is de lijn met vergelijking   y = -x . Er zijn vier waarden van t, met 0 <  t < 2π , waarvoor koorde AB evenwijdig is met l.
5p.	15.	Bereken exact deze vier waarden.

Diagonalen en gelijke hoeken.
Gegeven is een cirkel met een koordenvierhoek ABCD met diagonalen AC en BD. Diagonaal BD verdeelt hoek ADC in twee gelijke hoeken. Zie de figuur hiernaast. Voor deze koordenvierhoek geldt: AB en BC zijn even lang.
4p.	16.	Bewijs dit.
In de figuur hiernaast, is opnieuw een cirkel getekend met een koordenvierhoek ABCD. Er geldt nu: -  diagonaal BD verdeelt hoek ADC in twee gelijke hoeken; -  diagonaal AC verdeelt hoek BAD in twee gelijke hoeken. De diagonalen snijden elkaar in het punt E. De lijn door B en het middelpunt M van de cirkel snijdt diagonaal AC in het punt F. De lijn door C en M snijdt diagonaal BD in het punt G.
6p.	17.	Bewijs dat de punten E, F, M en G op één cirkel liggen.

UITWERKING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
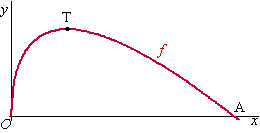
1.	f (x) = 3√x - x = 3x0,5 - x f ' (x) = 0,5 • 3x-0,5 - 1 f '(x) = 0   ⇒   0,5 • 3x-0,5 - 1 = 0 1,5x-0,5 = 1 x-0,5 = 2/3 √x  = 1,5 x = 1,52 = 21/4 y = 3√21/4 - 21/4 = 3 • 11/2 - 21/4 = 21/4.
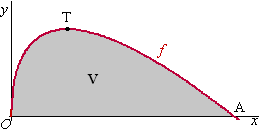
2.	f(x) = 0  geeft  3√x - x = 0 √x(3 - √x) = 0 Öx = 0  Ú 3 - √x = 0 x = 0  Ú  √x = 3 x = 0  Ú    x = 9  dus A is het punt  (9,0) De oppervlakte van V is:
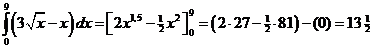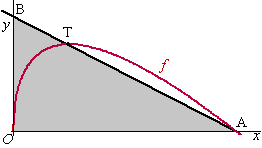
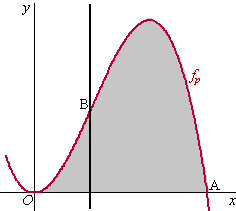
	A = (9, 0) en T = (21/4, 21/4) AT heeft helling  (2,25 - 0)/(2,25 - 9) = -1/3 AT is de lijn  y = -1/3x + b (9,0) invullen geeft  0 = -1/3 • 9 + b  dus  b = 3 en B = (0, 3) De oppervlakte van driehoek OAB is dan 1/2 • 9 • 3 = 131/2
3.
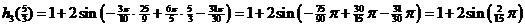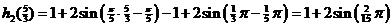	Dat is inderdaad gelijk.
4.
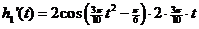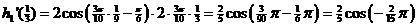	Maar omdat  cos(-α) = cos(α) is dat gelijk aan de gevraagde uitdrukking.
5.
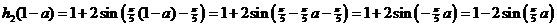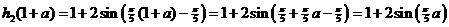	optellen:  h2(1 - a) + h2(1 + a)  = 1 - 2sin(p/5 • a) + 1 + 2sin(p/5 • a) = 2 Delen door 2 geeft inderdaad 1.
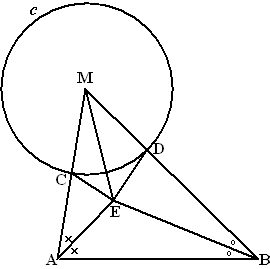
6.	Omdat de bissectrices van een driehoek elkaar in één punt snijden, en omdat BE en AE twee van die bissectrices zijn, is ME de derde bissectrice. Dus ∠CME = ∠DME CM = DM  (straal cirkel) ME = ME Dus de driehoeken MCE en MDE zijn gelijkvormig (ZZH) Dus is CE = DE
7.	Als je de grafiek van y = 2lnx een afstand a naar links verschuift krijg je de grafiek van y = 2ln(x + a) P:   y = 0 2ln(x + a) = 0 ln(x + a) = 0 x + a = 1 x = 1 - a Q:  x = 0 y = 2lna -OP = OQ geeft dan  1 - a = 2lna Y1 = -(1 - X)  en  Y1 = 2ln(X) en dan intersect geeft X = a = 1  en  X = a = 3,513 De gezochte oplossing (want a > 1)  is  a = 3,51
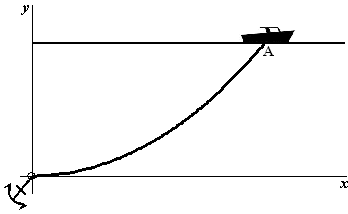
8.	f '(x) = 1/2a • (aeax - ae -ax) = 1/2a • a • (eax - e -ax) = 1/2 • (eax - e -ax) 1 + (f ')2 = 1 +  1/4 • (eax - e -ax)2 = 1 +  1/4 • ((eax)2 - 2eax • e -ax +  (e -ax)2 ) = 1 +  1/4(e2ax - 2 + e -2ax) =  1/4(e2ax - 2  + e -2ax + 4) =  1/4(e2ax + 2  + e -2ax) (1/2eax + 1/2e -ax)2 = (1/2(eax + e -ax) )2 = 1/4(eax + e -ax)2 = 1/4( (eax)2 + 2eax • e -ax + ( e -ax)2 ) = 1/4(e2ax + 2 + e -2ax) Dat is inderdaad gelijk.
9.
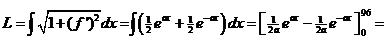	= (70e96/140 - 70e -96/140) - (70e0  - 70e-0) = 103,7 - 0 = 103,7 x = 96  geeft  y = 1/2a • (eax + e-ax - 2) = 70 • (e96/140 + e-96/140 - 2) = 70 • 0,4889 = 34,2 3 • 34,2 = 102,6 en dat is minder dan 103,7 dus de ankerketting voldoet aan de vuistregel.
10.
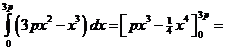	=  p(3p)3 - 1/4(3p)4   = 27p4 - 81/4p4 = 63/4p4  De oppervlakte van het rechterdeel is dan  63/4p4 - 3/4p4 = 6p4 6p4 is inderdaad 8 keer zo groot als 3/4p4
11.	B = (p, 2p3)  dus met Pythagoras geeft dat, dat BO = √(p2 + (2p3)2) AO = 3p Dus moet gelden:  √(p2 + (2p3)2) = 3p p2 + 4p6 = 9p2 4p6 - 8p2 = 0 4p2(p4 - 2) = 0 p = 0 ∨  p4 = 2 p = 0  ∨  p = ± 21/4 de gezochte oplossing is  p = 21/4
12.	B = (p, 2p3)  f '(x) = 6px - 3x2 f '(p) = 6p2 - 3p2 = 3p2  en dat is de helling van de buigraaklijn. De buigraaklijn is de lijn   y = 3p2x + b (p, 2p3) invullen:   2p3 = 3p2 • p + b 2p3 = 3p3 + b b = -p3 De buigraaklijn is de lijn y = 3p2x  - p3  Voor punt C geldt:  0 = 3p2x - p3 3p2x = p3 x = 1/3p Dus OC = 1/3p OA = 3p   dus  CA =  3p - 1/3p = 8/3p 8/3p is inderdaad acht keer zo groot als 1/3p
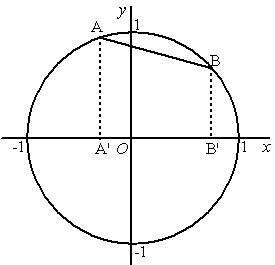
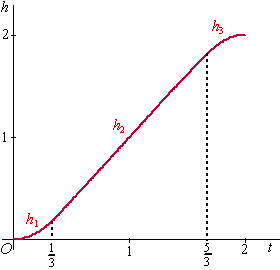
13.	A'B' = xB - xA = cost - cos3t   of   A'B' = xA - xB = cos3t - cost   plot  Y1 = cosX - cos3X en gebruik calc - maximum Dat geeft X = t = 0,9553 of X = 5,3279,  beiden  met maximum 1,5396 plot  Y1 = cos3X - cosX en gebruik calc - maximum Dat geeft X = t = 4,0969  of X = 2,1862,  beiden  met maximum 1,5396 De maximale lengte is dus 1,54
14.
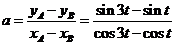	Gebruik de formules voor sint - sinu en cost - cosu. Dat geeft: sin3t - sint = 2sin(1/2(3t - t)) • cos(1/2(3t + t)) = 2sint • cos2t cos3t - cost = -2sin(1/2(3t + t)) • sin(1/2(3t - t)) = -2sin2t • sint invullen in a:
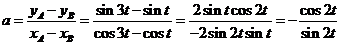15.	Als koorde AB evenwijdig is met l dan moet gelden a = -1 Dat geeft  cos2t = sin2t sin(1/2π - 2t) = sin2t 1/2π - 2t = 2t + k2π  ∨  1/2π - 2t = π - 2t + k2π 4t = 1/2π + k2π  ∨  1/2π = π  t = 1/8π + k • 1/2π Dat geeft in [0, 2π] de oplossingen  k = 1/8π,  k = 5/8π,  k = 9/8π en  k = 13/8π
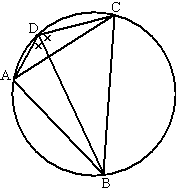
16.	∠BAC = ∠BDC  (beiden omtrekshoek van BC) ∠BCA = ∠BDA (beiden omtrekshoek van BA) Dus ∠BCA = ∠BAC Dus driehoek ABC is gelijkbenig met top B (gelijke basishoeken) Dus is BA = BC.
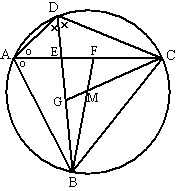
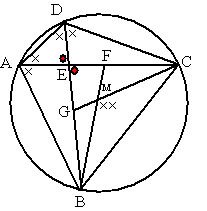
17.	de vier hoeken met een kruisje zijn allemaal gelijk (zie vraag 16) ∠BMC is het dubbele daarvan (middelpuntshoek van BC is dubbel zo groot als omtrekshoek van BC) ∠GMF is dus ook gelijk aan twee kruisjes (overstaande hoeken) De rode hoek is samen met twee kruisjes gelijk aan 180º (in driehoek AED). De rode hoek daartegenover dus ook (overstaande hoeken) Dus ∠GEF (rood) + ∠GMF (twee kruisjes) = 180º Dan is EGMF een koordenvierhoek.