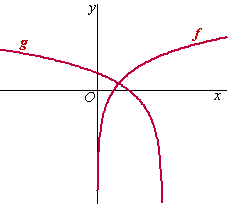VWO WB, 2001 - II

 

OPGAVE 1.
       
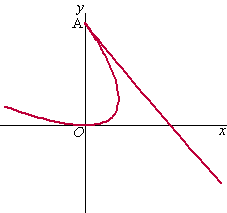
De functies f en g zijn gegeven door:
f(x) = ln2x
g(x) = ln(2 - x)

Hiernaast zijn de grafieken van f en g getekend met snijpunt S

     
8p. 1. Bereken de hoek waaronder de grafieken van f en g elkaar snijden; geef het antwoord in graden nauwkeurig.
     
De lijn met vergelijking x = p snijdt de grafiek van f in het punt A en de grafiek van g in het punt B.
       
6p. 2. Bereken p in het geval dat AB = ln2.
       
C is het punt van de grafiek van f waarvoor geldt dat de richtingscoëfficiënt van de lijn OC maximaal is.
       
6p. 3. Bereken de coördinaten van C.
       
De lijn met vergelijking y = 2 snijdt de grafiek van f in het punt P en de grafiek van g in het punt Q.
S' is de projectie van S op de lijn y = 2.
       
5p. 4. Toon aan dat voor de lengte van de lijnstukken S'Q en S'P geldt  S'Q = 2S'P.
       
OPGAVE 2.
         
Met domein [0, 2p] zijn de functies f en g gegeven door:
f(x) = 2sin2x  en   g(x) = 1 - cosx

Hiernaast zijn de grafieken van f en g getekend.

De vlakdelen ingesloten door de grafieken van f en g zijn in deze figuur aangegeven door A, B en C, en ingekleurd.

         
7p. 5. Bereken de maximale lengte van een verticaal lijnstuk in het vlakdeel A.
         
7p. 6. Bereken de oppervlakte van het vlakdeel B.
         
Op het venster van de grafische rekenmachine wordt de grafiek van de functie h, gegeven door  h(x) =  f(x)/g(x) weergegeven zoals in de figuur hiernaast.

     
5p. 7. Bewijs dat h(x) te schrijven is als h(x) = a + bcos(cx + d)
         
OPGAVE 3.
         
In de figuur hiernaast zijn drie grensvlakken van een afgeknot prisma OABC.DEFG getekend ten opzichte van een rechthoekig assenstelsel Oxyz. Van dit lichaam is gegeven:
OA = AB = 8, OC = CB = 6
AE = 2, CG = 10 en OD = 7
De opstaande ribben OD, AE, BF en CG zijn evenwijdig aan de z-as.

     
8p. 8. Bereken de hoek van de vlakken OBG en OABC; geef het antwoord in graden nauwkeurig.
     
Van een kegel ligt de top T in het vlak DEG.
De grondcirkel van deze kegel gaat door O, A, B en C.
     
8p. 9. Bereken de inhoud van deze kegel.
         
6p. 10. Teken punt F in de figuur hiernaast. Licht je werkwijze toe.
         
OPGAVE 4.
         
De kromme K is gegeven door:
x(t) = t(2 - t)2  en  y(t) = t2(3 - t)

Hiernaast is K getekend.

     
6p. 11. Bereken de coördinaten van de snijpunten van de lijn y = -x + 3 met de kromme K.
     
K heeft twee punten met de y-as gemeen:  O en A.
     
7p. 12. Bereken de hoek die de kromme K maakt met de y-as in het punt A. Geef het antwoord in graden nauwkeurig.
         
Voor elke a ∈ R is de kromme Ka gegeven door:   x(t) = t(2 - t)2  en   y(t) = t2 (a - t)

Voor a = 3 krijgen we de kromme K van hierboven.
Hieronder zijn achtereenvolgens  K1, K2 en K4 getekend.
         

         
Het lijkt erop dat voor a ≠ 3 alle Ka de y-as raken.
         
6p. 13. Bewijs dat alle Ka voor a ≠ 3 de y-as raken.
         
5p. 14. Bewijs dat K2 symmetrisch is ten opzichte van de lijn y = x
         

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.