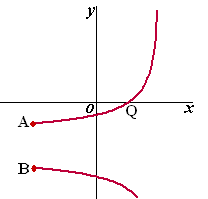OPGAVE 1.
Gegeven is de functie  f:  x  →│ln(x + 4)│
4p.	1.	Geef aan hoe men de grafiek van f kan afleiden uit de grafiek van  x → lnx en teken de grafiek van f.
De grafiek van f heeft één punt met de x-as gemeen.
5p.	2.	Bereken de hoek die de raaklijnen aan de grafiek van f in dat punt met elkaar maken.
De lijn y = p snijdt de grafiek van f in de punten A en B.
7p.	3.	Bereken p in het geval dat AB = 11/2
V is het begrensde vlakdeel dat ingesloten wordt door de grafiek van f, de x-as en de y-as.
7p.	4.	Bereken de inhoud van het omwentelingslichaam dat ontstaat als V om de y-as wentelt.

OPGAVE 2.
De kromme K is gegeven door:
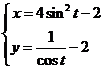waarbij t ∈ [0, 2π] \ {1/2π, 11/2π} Hiernaast is K getekend.
5p.	5.	Bereken de coördinaten van de snijpunten van K met de coördinaat-assen.
A en B zijn de eindpunten van de beide takken van K.
4p.	6.	Bereken de coördinaten van A en B.
P is een punt van de bovenste tak van K. m is de richtingscoëfficiënt van de raaklijn aan K in P.
5p.	7.
Q is het snijpunt van K met de x-as.
4p.	8.	Toon aan dat de lijn BQ raaklijn is aan K.

OPGAVE 3.
Voor  p > 0 zijn gegeven de functies:
Hiernaast is de grafiek van g1 getekend.
9p.	9.	Onderzoek f1 en teken de grafiek van f1 in de figuur hiernaast. Bepaal hierbij ook de eventuele snijpunten van de grafieken van f1 en g1.
Voor elke p > 0 liggen de toppen van de grafiek van fp zowel op de verticale asymptoten van de grafiek van gp als op de kromme  y = 1/x.
6p.	10.	Bewijs dit.
De raaklijn aan de grafiek van fp in O(0,0) snijdt de grafiek van gp in het punt A met positieve x-coördinaat. De projectie van A op de x-as is het punt B.
9p.	11.	Bewijs dat de oppervlakte van het vlakdeel dat ingesloten wordt door de grafiek van fp, de x-as en de lijn AB onafhankelijk is van p.

OPGAVE 4.
In de figuur hiernaast is de regelmatige zeszijdige piramide T.ABCDEF getekend. De middens van de ribben BT en FT zijn achtereenvolgens M en N. Gegeven is verder dat AB = 6 en dat de afstand van T tot het grondvlak ABCDEF gelijk is aan 6√3.
6p.	12.	Bereken de hoek tussen de lijn AM en het vlak ABCDEF
6p.	13.	Teken de doorsnede van het vlak AMN met de piramide.
6p.	14.	Bereken de kortste weg van A naar C over de zijvlakken van de piramide via de ribbe BT.
7p.	15.	Onderzoek of er een bol bestaat door de hoekpunten van het lichaam BCEF.MN.

UITWERKING
1.
2.	90º
3.	p = ln2
4.	p(16ln4 - 16,5)
5.	(1,0)
6.	A(-2, -1)  en  B(-2, -3)
7.
8.
9.	snijpunt (0,0)
10.
11.
12.	45º
13.	3√15
14.	JA