OPGAVE 1.
De kromme K is gegeven door:  x = t2 - 3  en  y = t3 - 3t
9p.	1.	Teken K, bereken daartoe eerst de coördinaten van:
		• de snijpunten van K met de coördinaatassen. • de punten van K waarin de raaklijn aan K evenwijdig is met één van de coördinaatassen.
De coördinaten van de punten van K voldoen aan de vergelijking  y2 = x2(x + 3)
3p.	2.	Toon dit aan.
V is het vlakdeel, in gesloten door K.
5p.	3.	Bereken de inhoud van het lichaam dat ontstaat door V te wentelen om de x-as.
De lijn y = ax heeft precies één punt met K gemeenschappelijk.
6p.	4.	Bereken voor welke waarden van a dit het geval is.

OPGAVE 2.
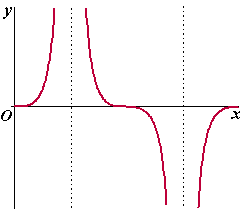
met domein [0, 2π] \ {1/2π, 11/2π} Hiernaast is de grafiek van f getekend. Op hetzelfde domein is g de functie  g : x → -3/2tanx
8p.	5.	Los op:  f(x) = g(x)
Uit de figuur blijkt dat de grafiek van f dalend is voor  1/2π < x < 11/2π.
7p.	6.	Bewijs dit.
V is het vlakdeel begrensd door de grafiek van f, de x-as en de lijn  x = 11/4π
2p.	7.
7p.	8.	Bereken nu de oppervlakte van V.

OPGAVE 3.
In de figuur hiernaast is de regelmatige vierzijdige piramide T.ABCD getekend. De middens van de ribben AT, BT, CT en DT zijn achtereenvolgens K, L, M en N. P is het snijpunt van AN en DK Q is het snijpunt van BM en CL. Gegeven is verder dat AB = BC = 6 en dat de afstand van T tot het vlak ABCD ook gelijk is aan 6.
7p.	9.	Bereken de inhoud van het lichaam ABCD.KL
4p.	10.	Arceer in de figuur hieronder de loodrechte projectie van het lichaam KLMN.PQ op het grondvlak ABCD.
7p.	11.	Bereken de afstand van de lijn MN tot vlak ABT.
De bol met middelpunt T en straal TK snijdt de zijvlakken van de piramide volgens een aantal cirkelbogen.
7p.	12.	Onderzoek door een berekening of de weg van K naar M via deze cirkelbogen langer is dan de weg via de cirkel door K, L en M.

OPGAVE 4.
Voor elke a ∈ R\{0} is de functie fa gegeven door:
In de figuur hiernaast is de grafiek van fa getekend voor enkele waarden van a.
5p.	13.	Bereken voor welke waarde van a de maximale y-coördinaat van een punt op de grafiek van fa gelijk is aan 3.
6p.	14.	Bereken de waarden van a waarvoor de grafiek van fa de x-as snijdt onder een hoek van 30º
Neem a = 2. De lijn y = p snijdt de y-as in het punt A en de grafiek van f2 in de punten B en C zo dat AC = 2AB.
7p.	15.	Bereken p.

UITWERKING
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.