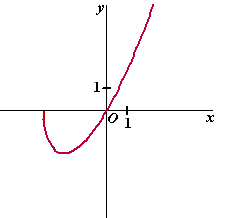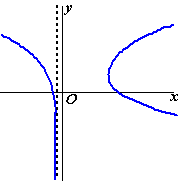VWO WB, 1997 - II

 

OPGAVE 1.
       
Met domein [-3, →〉 is gegeven de functie  f:  x →  x√(x + 3)  en
met domein  [-3, →〉 \ {0} de functie

De grafiek van f is in de figuur hiernaast getekend.
     
4p. 1. Bereken het bereik van f.
     
6p. 2. Bereken de coördinaten van de gemeenschappelijke punten van de grafieken van f en g.
       
10p. 3. Onderzoek g en teken de grafiek van g in de figuur hierboven.
       
Het gesloten vlakdeel begrensd door de grafieken van f en g wordt gewenteld om de x-as.
       
7p. 4. Bereken de inhoud van het omwentelingslichaam dat zo ontstaat.
       
OPGAVE 2.
       
Met domein [0, π] is de functie f gegeven door:

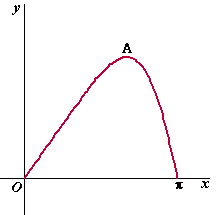
In de figuur hiernaast is de grafiek van f getekend.

Het punt A is de top van de grafiek van f.
     
5p. 5. Bereken de coördinaten van A.
     
6p. 6. Bereken de oppervlakte van het vlakdeel begrensd door de grafiek van  f en de x-as.
       
Voor 1 < a < 3  heeft de grafiek van de functie   x →  asinx  drie punten met de  grafiek van f gemeen.
       
7p. 7. Toon dit aan.  
       
OPGAVE 3.
       
De kromme K die in de figuur hiernaast is getekend, is gegeven door:

waarbij t ∈ 〈←, -1〉 ∪ 〈1, →〉 
     
7p. 8. Bereken de coördinaten van de punt(en) van K waar de raaklijn aan K evenwijdig is aan de y-as.
       
Er is een waarde van p ∈ R  zo dat de lijn y = x + p  de kromme K raakt.
       
7p. 9. Bereken p.
       
Voor elke a ∈ R  snijdt de lijn y = a de kromme K in de punten Pa en Qa.
Ma is het midden van lijnstuk PaQa.
       
8p. 10. Toon aan dat de x-coördinaat van Ma gelijk is aan  1 + e-a
       
OPGAVE 4.
       
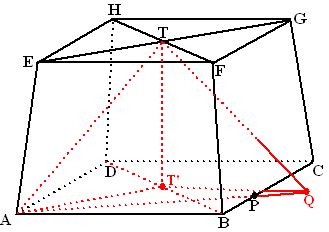
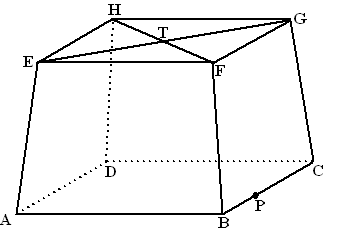
Van de afgeknotte piramide ABCD.EFGH, hiernaast getekend in scheve parallelprojectie, is gegeven:
Het grondvlak ABCD is een vierkant met zijde 7, het bovenvlak EFGH is een vierkant met zijde 6,  en de hoogte is 5.
Lijn DH staat loodrecht op grond- en bovenvlak.
     
5p. 11. Bereken de inhoud van ABCD.EFGH.
     
b is de bol met middelpunt F en straal √26.
O is de oppervlakte van het gedeelte van vierkant ABCD dat buiten b ligt.
     
6p. 12. Bereken O.
       
T is het snijpunt van EG en FH.
De lijn AT snijdt vlak ABCD onder een hoek van α graden.
       
5p. 13. Bereken α.  
       
P is een punt van ribbe BC (zie de figuur).
V is het vlak door de punten A, T en P.
Behalve de lijn AT is er nog een lijn door T die in V ligt en een hoek van α graden maakt met vlak ABCD.
       
7p. 14. Teken deze lijn in de figuur hierboven. Licht je werkwijze toe.
       

 

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14. Kies Q zo dat  AT' =  QT'
Dan maakt QT ook een hoek a met vlak ABCD.