| OPGAVE 1. | |||
|
Gegeven is de functie f:
x → x + 3 - 4√x
met domein [0, →〉
Ten opzichte van een assenstelsel Oxy is K de grafiek van f. |
|||
| 8p. | 1. | Onderzoek f en teken K. | |
| 6p. | 2. | Bereken de oppervlakte van de driehoek gevormd door de x-as en de raaklijnen aan K in de punten waar K de x-as snijdt. | |
| V is het vlakdeel begrensd door K en de lijn y = 3. | |||
| 7p. | 3. | Bereken in gehelen nauwkeurig de inhoud van het lichaam dat ontstaat door V te wentelen om de lijn y = 3. | |
| OPGAVE 2. | |||
| Ten opzichte van
een assenstelsel Oxy is de kromme K gegeven door: x= ln |t + 1| en y = ln | t - 1 | waarbij t ≠ -1 en t ≠ 1. Er zijn drie snijpunten van K met de coördinaatassen. |
|||
| 8p. | 4. | Bereken de richtingscoëfficiënten van de raaklijnen in deze snijpunten. | |
| K heeft een horizontale, een verticale en een scheve asymptoot. | |||
| 5p. | 5. | Stel een vergelijking op van elk van deze asymptoten. | |
| 5p. | 6. | Teken K. | |
| 6p. | 7. | Bewijs dat K symmetrisch is ten opzichte van de lijn y = x. | |
| OPGAVE 3. | |||
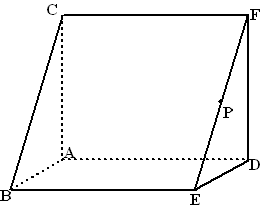
| Van het rechte
prisma ABC.DEF dat in scheve parallelprojectie hiernaast is getekend is
gegeven: ÐBAC = 90º, AB = 6, AC = 8 en AD = 10 P is het midden van EF. Vlak ACP verdeelt het prisma in twee delen. |
|
||
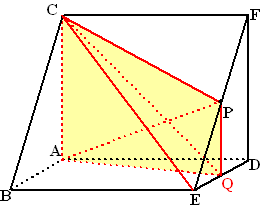
| 8p. | 8. | Bereken de verhouding van de inhouden van die twee delen. | |
| Een bol raakt vlak ABC en gaat door D, E en F. | |||
| 8p. | 9. | Bereken de straal van deze bol. | |
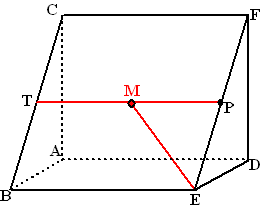
| 8p. | 10. | Teken in de figuur de lijn door P die lijnstuk AC snijdt en lijn CF kruist op een afstand van 2. Licht je werkwijze toe. | |
| OPGAVE 4. | |||
|
|
|||
| 7p. | 11. | Los op f(x) ≥ 4 cosx. | |
| Verder is gegeven de differentiaalvergelijking D: dy/dx = 2y2 • sin2x | |||
| 4p. | 12. | Onderzoek of f een oplossing van D is. | |
| Voor een oplossingsfunctie g van D geldt: g(π/2) = 1 | |||
| 4p. | 13. | Toon aan dat g(π/2) een maximum is. | |
| 6p. | 14. | Stel een functievoorschrift op van g. | |