OPGAVE I.
Voor elke p ∈ R is gegeven de functie  fp :  x  → x4 - 4x3 + px2  met domein R. Ten opzichte van een rechthoekig assenstelsel Oxy is  Fp  de grafiek van fp.
1.	Onderzoek f4 en teken F4.
De lijn y = mx  waarbij  m ∈ R, en F4 hebben precies drie punten gemeenschappelijk.
2.	Bereken m.
3.	Bereken p in het geval dat fp  een oplossing is van de differentiaalvergelijking    x • dy/dx = 4x3 - 3x2 + 4y
OPGAVE 2.
Voor elke p ∈ N+ is gegeven de functie  fp : x → p - 1 + cospx  met domein  [0, 2π]. Ten opzichte van een rechthoekig assenstelsel Oxy is Fp de grafiek van fp.
4.	Onderzoek voor welke p geldt:  Fp raakt de x-as.
5.	Onderzoek voor welke p de lijn y = 1/2p  en Fp minstens vier punten gemeenschappelijk hebben.
V is het vlakdeel ingesloten door F3, de x-as, de y-as en de lijn  x = 2π.
6.	Bereken de inhoud van het omwentelingslichaam dat ontstaat door V te wentelen om de x-as.
OPGAVE 3.
Ten opzichte van een rechthoekig assenstelsel Oxy is de kromme K gegeven door: x = ln | t |   en  y = t2 - 4t  waarbij  t ∈ R\{0}
7.	Stel een vergelijking op van de asymptoot van K.
8.	Bereken de coördinaten van de snijpunten van K en de coördinaatassen.
9.	Bereken de coördinaten van het punt van K waarin de raaklijn aan K evenwijdig is aan de x-as.
10.	Teken K.
De lijn x = a  waarbij  a ∈ R  snijdt K in de punten A en B. Het punt M is het midden van lijnstuk AB.
11.	Stel een vergelijking op van de verzameling van de punten M.
De lijn door M evenwijdig aan de x-as snijdt K in de punten C en D.
12.	Bewijs dat M voor elke a ∈ R  het midden is van lijnstuk CD.
OPGAVE 4.
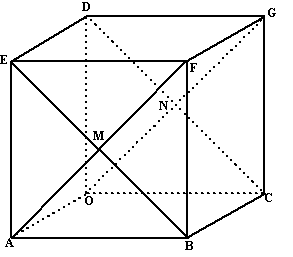
Van de kubus  OABC.DEFG die hieronder tweemaal is afgebeeld hebben de ribben lengte 6. Verder is gegeven: Punt M is het snijpunt van de lijnen AF en BE. Punt N is het snijpunt van de lijnen CD en OG. Punt P doorloopt lijnstuk DE en punt Q doorloopt lijnstuk AB.
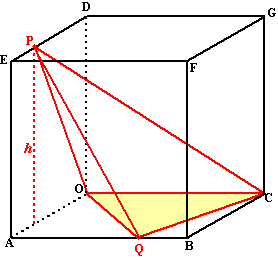
13.	Bewijs dat de inhoud van het viervlak OPQC constant is.
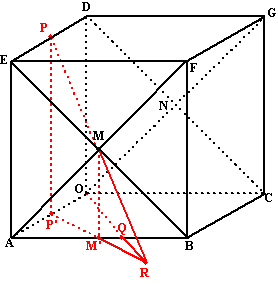
Neem voor P het midden van lijnstuk DE. Q ligt zo op lijnstuk AB dat de lijnen PM en OQ elkaar snijden.
14.	Teken Q in de figuur hieronder.
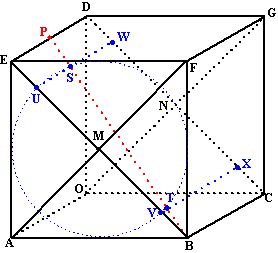
Neem voor P weer het midden van lijnstuk DE. De lijn BP snijdt de cilinder(mantel) met as MN en straal 3 in de punten S en T.
15.	Teken S en T in de figuur hieronder.
16.	Bereken ST.

UITWERKING
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.