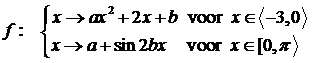VWO WB, 1988 - I
 
OPGAVE 1.
   
Met domein R is gegeven de functie  f :  x →  x + e-x
Ten opzichte van een rechthoekig assenstelsel Oxy is F de grafiek van f.
       
1. Bereken het bereik van f
       
2. Stel een vergelijking op van de asymptoot van F.
       
3. Teken F.
       
4. Stel een vergelijking op van de lijn door O die F raakt.
       
Het vlakdeel ingesloten door F, de x-as, de y-as en de lijn x = -1 wentelt om de x-as.
       
5. Bereken de inhoud van het omwentelingslichaam.
       
OPGAVE 2.
       
Gegeven is de op  〈-3, π〉 differentieerbare functie:
       
 

       
Ten opzichte van een rechthoekig assenstelsel Oxy is F de grafiek van f.
       
6. Bewijs dat a = b = 1
       
7. Onderzoek f  verder.
       
8. Bereken de coördinaten van de buigpunten van F.
       
9. Teken F.
       
V is het vlakdeel in gesloten door F en de x-as.
       
10. Bereken de oppervlakte van V.
       
De lijn door (0,1) en (p, 0) met  p  Î 〈0, 3/4π〉 verdeelt V in twee vlakdelen V1 en V2; V1 bevat het punt (0, 1/2)
De oppervlakten van V1 en V2 verhouden zich als 2 : 3
       
11. Bereken p.
       
OPGAVE 3.
       
Ten opzichte van een rechthoekig assenstelsel Oxy is de kromme K gegeven door:
x = t2 - t - 2  en   y = t2 + t + 1/4,  waarbij  t  ∈ R
       
12. Bereken de coördinaten van de gemeenschappelijke punten van K en de coördinaatassen.
       
13. Bereken de coördinaten van de punten van K waarin de raaklijn aan K evenwijdig is aan de x-as of aan de y-as.
       
14. Onderzoek welke waarden de richtingscoëfficiënten van de raaklijnen aan K kunnen aannemen.
       
15. Teken K.
       
Een vierhoek waarvan de hoekpunten op K liggen heeft de y-as als symmetrie-as.
       
16. Bereken de oppervlakte van deze vierhoek.
       
OPGAVE 4.
       
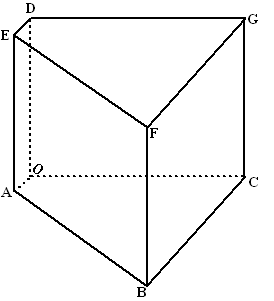
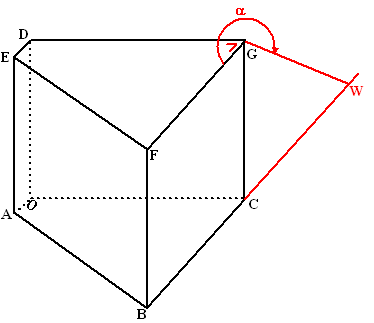
Van het prisma dat hieronder staat afgebeeld is gegeven:
∠AOC = ∠AOD = ∠COD = 90º
BC // AO
BC = CO = 8, AO = 1 en DO = 4.
       

       
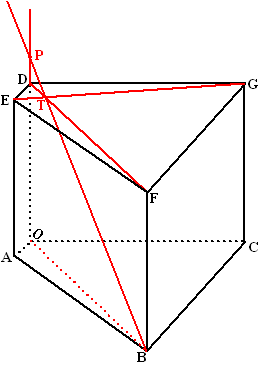
De lijn l  gaat door B, snijdt de lijn EG en snijdt de lijn OD in punt P.
       
17. Bereken OP.
       
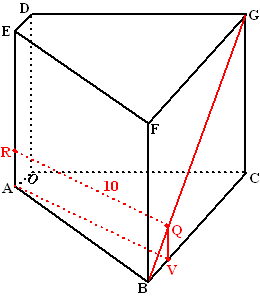
Punt Q ligt op het lijnstuk BG en punt R ligt op het lijnstuk AE.
Lijn QR is evenwijdig aan het vlak ABC.
QR = 10.
       
18. Bereken de afstand van lijn QR en het vlak ABC.
       
Vierhoek DEFG is een deksel dat kan scharnieren om de lijn DG.
Het deksel wordt opengeklapt tot het achterover met de punt op het vlak ABC rust: daar ligt het punt S.
       
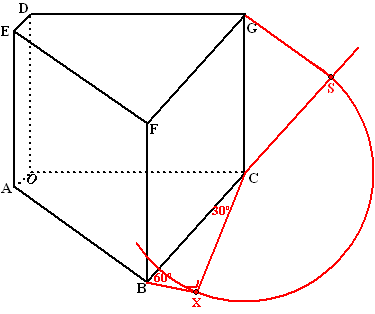
19. Bereken over welke hoek het deksel draaide.
       
Bovenstaande figuur is een parallelprojectie van het prisma waarbij vierhoek OCGD evenwijdig is aan het vlak van de tekening.
       
20. Teken punt S in deze figuur.  Licht je werkwijze toe.
       
UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  

   
18.  

   
19.  
   
20.  
   
21.  
   
22.  
   
23.