| 1. | Met domein R+
is voor elke p ∈ R+ gegeven
de functie fp: x
→ p√x
- lnx Ten opzichte van een rechthoekig assenstelsel Oxy is Fp de grafiek van fp. |
||
| a. | Bereken de extreme
waarde van f2. Stel een vergelijking op van de asymptoot van F2. Bereken de co÷rdinaten van het buigpunt van F2. Teken F2. |
||
| b. | Stel een vergelijking op van de verzameling van de punten van Fp waarin de raaklijn aan Fp evenwijdig aan de x-as is. | ||
| c. | O(k) is de
oppervlakte van het vlakdeel ingesloten door F2, de x-as,
de lijn x = 1 en de lijn x = k, waarbij k ∈ 〈0, 1〉. |
||
|
|
|||
| 2. | Ten opzichte van
een rechthoekig assenstelsel Oxy is de kromme K gegeven door: x = 1/4t2 - 3t en y = t + 4/t - 5, waarbij t ∈ R. |
||
| a. | Bereken de
snijpunten van K en de co÷rdinaatassen. Onderzoek of K een asymptoot heeft. |
||
| b. | Bereken in graden
nauwkeurig de hoek van K en de y-as. Bereken de co÷rdinaten van de punten van K waarin de raaklijn aan K evenwijdig is aan de x-as of aan de y-as. |
||
| c. | Bewijs dat K zichzelf snijdt in het punt (-1,7) | ||
| 3. | Met domein [-1/2π,
1/2π]
is gegeven de functie f : x
→ 3sin3x Ten opzichte van een rechthoekig assenstelsel Oxy is F de grafiek van f |
||
| a. | Onderzoek f. Bereken het aantal buigpunten van F. Teken F. |
||
| b. | Met domein [-1/2π,
11/2π]
is de functie g : x
→ acos3x
+ bcosx, waarbij a ∈ R en b ∈ R, een primitieve van f. Bereken a en b. Bereken de oppervlakte van het vlakdeel ingesloten door F en de x-as. |
||
| c. | De grafiek van de
functie x → pcosx
waarbij p ∈ R+
snijdt F loodrecht. Bereken p. |
||
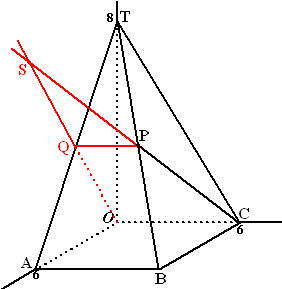
| 4. | Ten opzichte van een rechthoekig assenstelsel Oxyz is de piramide T.OABC gegeven door O(0,0,0), A(6,0,0), B(6,6,0), C(0,6,0) en T(0,0,8) | ||
| a. | Punt P is het
midden van lijnstuk BT. De lijn PC snijdt het vlak OAT in het punt S. Teken in een ruimtefiguur de piramide T.OABC en construeer het punt S. Bereken de co÷rdinaten van S. |
||
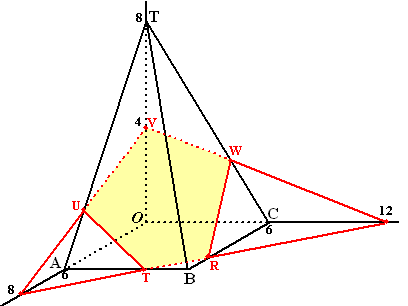
| b. | De loodrechte
projectie op het Oxy-vlak van de doorsnede van de piramide met
het vlak met vergelijking x + 2/3y + 2z = 8 is een vijfhoek V. Bereken de oppervlakte van V. |
||
| c. | Punt Q is het
midden van lijnstuk AT. De lengte van de kortste verbinding van Q en C via het lijnstuk OT is a. De lengte van de kortste verbinding van Q en C via het lijnstuk OA is b. Bereken a. Construeer een lijnstuk met lengte b. |
||