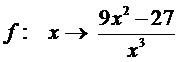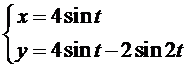| 1. | Met domein R\{0} is gegeven de functie: | ||
|
|
|||
| Ten opzichte van een rechthoekig assenstelsel is Kf de grafiek van f. | |||
| a. | Onderzoek f en teken Kf. | ||
| b. | Bereken de oppervlakte van het vlakdeel ingesloten door Kf, de x-as en de lijn x = 3. | ||
| c. | Voor welke p ∈ R heeft Kf precies vier punten met de lijn y = px gemeen? | ||
| 2. | Gegeven is de differentiaalvergelijking D: (y - x2 + x )dy = (2y - 2x + 2)dx | ||
| a. | V is de verzameling van punten
waarin het lijnelement van D een negatieve richtingscoŽfficiŽnt heeft. Maak een tekening van V. |
||
| b. | Van een in R differentieerbare
functie f is gegeven: de grafiek van f is een
integraalkromme van D en f heeft een extreme waarde voor x
= 0. Bereken die extreme waarde. Is dit een maximum of een minimum? Onderzoek of f een tweedegraads functie kan zijn. |
||
| c. | Voor elke p ∈ R is lp de
lijn met vergelijking y = -2x + p Voor welke waarden van p raakt lp ten minste ťťn integraalkromme van D? |
||
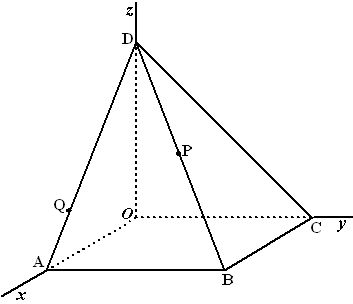
| 3. | Ten opzichte van
een rechthoekig assenstelsel Oxyz zjin gegeven de punten
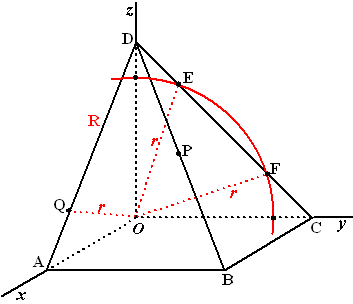
A(8,0,0), B(8,8,0), C(0,8,0) en D(0,0,8). Deze punten zijn de hoekpunten van een vierzijdige piramide D.ABCO. Punt P is het midden van ribbe BD en punt Q ligt op ribbe AD zo dat AQ : QD = 1 : 3. V is het vlak door P, evenwijdig aan de lijn BQ en evenwijdig aan de lijn DO. |
||
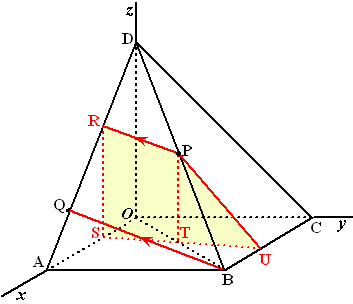
| a. | Teken in de figuur hieronder de
doorsnede van V met de piramide. Geef daarbij een korte toelichting. Stel een vergelijking op van V. |
||
|
|
|||
| Een bol met middelpunt O en straal OQ snijdt de lijn CD in de punten E en F. | |||
| b. | Teken in de onderstaande figuur
de doorsnede van deze bol met het vlak x = 0. Bereken EF. |
||
|
|
|||
| c. | Onderzoek hoeveel punten deze bol met de lijn BD gemeen heeft. | ||
| 4. | Ten opzichte van een rechthoekig assenstelsel Oxy is voor t ∈ R de kromme K gegeven door: | ||
|
|
|||
| a. | Welke waarden kan x
aannemen? Welke waarden kan y aannemen? |
||
| b. | Bewijs dat de x-as een
raaklijn is van K. Teken K. |
||
| c. | De lijn x = p, met
p ∈ R+ , snijdt K in de
punten A en B zo, dat AB = 4. Bereken p. |
||