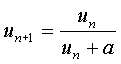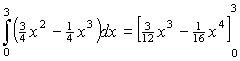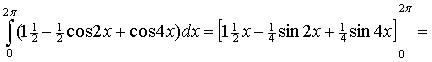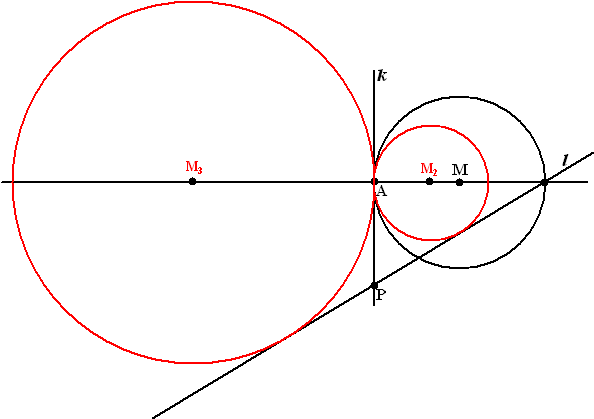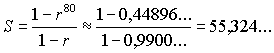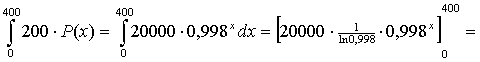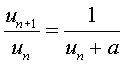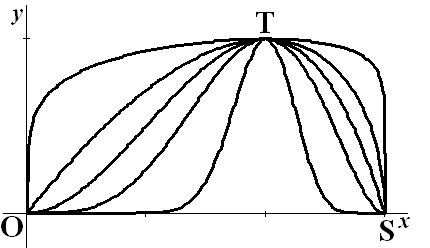
VWO WISKUNDE B1,2    2004 - I
Machten van een derdegraadsfunctie
Gegeven is de functie  f (x) = 3/4x2 - 1/4x3  op het domein [0,3]
V is het gebied, ingesloten door de grafiek van f en de x-as.
5p 1. Bereken algebraïsch de exacte waarde van de oppervlakte van V.

 
Op het domein [0,3] bekijken we de functies  gp(x) = (f (x))p = (3/4x2 - 1/4x3)p,  waarbij p > 0
In de figuur hieronder zijn de grafieken van gp getekend voor  p = 10, p= 2, p = 1,  p = 0,5 en p = 0,1. Al deze grafieken gaan door de punten O(0,0), T(2,1) en S(3,0)
Voor elke positieve waarde van p gaat de grafiek van gp door O, T en S.
3p 2. Toon dat aan.

 
Krasloten
Deze opgaven gaat over krasloten waarmee je 3 euro of 6 euro of niets kunt ontvangen. Elk kraslot heeft drie vakjes die je open kunt krassen. Zie de figuur hieronder.
In één van de vakjes is een MIN (-) verborgen, in de andere twee een PLUS (+).
Je kunt het kraslot inleveren na één vakje of na twee vakjes te hebben opengekrast. Voor elke opengekraste PLUS ontvang je drie euro, maar als je de MIN hebt opengekrast is het lot waardeloos geworden. Zie de figuur hieronder.
Bij de mensen die krasloten kopen onderscheiden we twee typen krassers:
  • waaghalzen: krassen een tweede vakje open als het eerste vakje een PLUS oplevert.
  • angsthazen : krassen één vakje open en stoppen.
Je kunt je afvragen welk type krasser het slimst is.
4p 3. Bereken voor zowel de waaghalzen als de angsthazen welk bedrag zij naar verwachting per opengekrast lot zullen ontvangen.

 
Bij een bepaalde kiosk is gebleken dat 65% van de krassers een waaghals is en 35% een angsthaas.
Op zekere dag komen 500 mensen een lot kopen bij deze kiosk en krassen het open.
5p 4. Bereken hoeveel van deze mensen naar verwachting niets uitbetaald krijgen.

 
Van een groep mensen bestaande uit 65 waaghalzen en 35 angst hazen heeft ieder precies één lot opengekrast.
6p 5. Bereken de kans dat uiteindelijk meer dan 60 mensen van deze groep precies één vakje hebben opengekrast.

 
Een verzameling functies
Op het domein [0,2π] zijn gegeven de functies:
fn (x) = 1 + sin2x + cos nx  waarbij n  een positief geheel getal is.
De grafiek van fn gaat voor bepaalde waarden van n door het punt (1/6π , 1/4)
4p 6. Onderzoek voor welke waarden van n tussen 0 en 50 dit geldt.

 
f4(x)  is te schrijven als  f4(x) = 11/2 - 1/2cos 2x + cos 4x
3p 7. Toon aan dat dit juist is.

 
Gegeven is de rechthoek OABC met  A(2π , 0) en C(0,3)
De grafiek van f4 verdeelt deze rechthoek in twee gebieden.
7p 8. Toon aan met behulp van integreren dat deze twee gebieden exact dezelfde oppervlakte hebben.

 
Cirkel met lijnen
Gegeven is de cirkel c met middellijn AB en middelpunt M. Lijn k raakt c in A. Lijn l is een lijn door B die c in nog een ander punt D (ongelijk aan A) snijdt. P is het snijpunt van k en l. Zie de figuur hiernaast.

Er zijn twee cirkels die l raken en bovendien cirkel c in A raken.
5p 9. Teken in de figuur de twee middelpunten van deze twee cirkels. Licht je werkwijze toe.

 
We gaan uit van dezelfde situatie als hierboven.
Verder is gegeven dat ∠AMP = ∠APD. S is het snijpunt van AD en PM. Zie de figuur hiernaast.
7p 10. Bewijs dat AS = PS = MS.

 
Grondprijs
Een nieuw industrieterrein grenst aaneen recht kanaal en heeft de vorm van een rechthoek OABC.
OA = 4500 m en OC = 200 m. Zie de figuur hiernaast.

De grondprijs is afhankelijk van de afstand tot het kanaal: hoe dichter bij het kanaal, hoe duurder de grond.
Het verband tussen de grondprijs P (in euro per m2) en de afstand tot het kanaal x (in meters) wordt gegeven door de formule:

P(x) = 100 • 0,998x
De punten waar P gelijk is aan 63 liggen op een lijn. Deze lijn is in de figuur hierboven getekend.
4p 11. Teken in deze figuur de lijn waarop alle punten liggen waar P gelijk is aan 55. Licht je antwoord toe.

 
Iemand wil een schatting maken van de grondprijs van het hele terrein.
Daartoe verdelen we rechthoek OABC in rechthoekjes met lengte 200 meter en breedte Dx meter. In de figuur hiernaast is één zo'n rechthoekje getekend op x meter van het kanaal. De totale grondprijs is dan bij benadering de som van de grondprijzen van deze rechthoekjes.

5p 12. Bereken op deze manier de totale grondprijs als Δx = 5 meter.
Geef je antwoord in miljoenen euro, afgerond op twee decimalen.

 
De totale grondprijs is nauwkeuriger te berekenen met behulp van een integraal.
4p 13. Bereken de totale grondprijs met behulp van deze integraal.

 
Ingesloten
In de figuur hiernaast is een vierkant getekend met middelpunt M en zijden 2. In het vierkant zijn de horizontale en de verticale symmetrieas getekend. Op afstand a van de middens van de zijden liggen de punten A, B, C en D. Hierbij is  0 < a < 1.
We gaan een rij punten op de symmetrieassen construeren.
  • Als startpunt P0 kiezen we het midden van de rechterzijde.
  • P0A snijdt een as in P1
  • P1B snijdt een as in P2
  • P2C snijdt een as in P3
  • P3D snijdt een as in P4
enzovoort.
In de figuur hiernaast zijn de eerste drie stappen (dus tot en met punt P3) uitgeboerd. Bij elke stap ontstaan twee gelijkvormige driehoeken.
De lengte van MPn noemen we un  (n = 0, 1, 2, 3, ...).  Dus  u0 = MP0 = 1

Neem a  = 1. Dan liggen de punten A, B, C en D op de hoekpunten van een vierkant.
5p 14. Bereken voor dit geval  u1, u2 en u3.

 
We kiezen nu voor a een getal tussen 0 en 1.
In de figuur hiernaast zie je hoe uit un de volgende term un+1 wordt gevonden.
5p 15. Toon aan dat de volgende recursieve betrekking geldt:

 
We kiezen nu  a = 2/3.
Het proces wordt eindeloos herhaald. Er is een vierkant rond M dat steeds nauwer wordt ingesloten.
Zie de figuur hiernaast.
5p 16. Bereken de oppervlakte van dit vierkant exact. Licht je antwoord toe met een berekening.

 
Ellipsen in een vierkant
Gegeven is een vierkant waarvan één diagonaal verticaal is. Binnen dit vierkant tekenen we ellipsen die er precies in passen: de ellipsen raken aan de vier zijden van het vierkant. In de figuur hiernaast zie je het vierkant met daarin enkele mogelijke ellipsen getekend.

In de figuur hiernaast is het vierkant nogmaals getekend met daarin één van de hierboven beschreven ellipsen. P, Q, R en S zijn de hoekpunten van het vierkant. A, B, C en D zijn de raakpunten van de ellips met het vierkant. F1 en F2 zijn de brandpunten van de ellips. De lijn PR is een symmetrieas van deze figuur.

Er geldt:  ∠PAF1 = ∠QBF1
5p 17. Bewijs dit.

 
PAF1B is een koordenvierhoek.
4p 18. Bewijs dit.

 
OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. f(x) = 0  ⇒  x2 • (0,75 - 0,25x) = 0  ⇒  x = 0   V  x = 3 

= (81/12 - 81/16) - (0) = 27/16 (=1,6875)  
2. gp(0) = (0,75 • 02 - 0,25 • 03)p = 0p = 0 dus de grafieken gaan allemaal door (0,0)
gp(2) = (0,75 • 22 - 0,25 • 23)p = 1p = 1 dus de grafieken gaan allemaal door (2,1)
gp(3) = (0,75 • 32 - 0,25 • 33)p = 0p = 0 dus de grafieken gaan allemaal door (3,0)
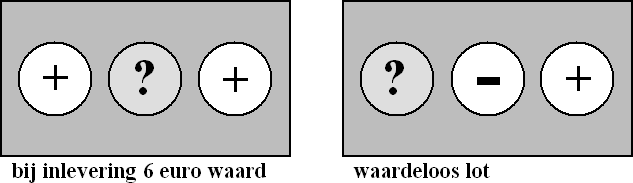
3. waaghals:   P(prijs) = P(++) = 2/3 • 1/2 = 1/3 dus de verwachtingswaarde is 6 • 1/3 + 0 • 2/3 = 2 euro
angsthaas:  P(prijs) = 2/3  dus de verwachtingswaarde is  3 • 2/3 + 0 • 1/3 = 2 euro
4. De kans dat een waaghals niets krijgt is 2/3 en voor een angsthaas is dat 1/3
2/3 van de waaghalzen is  2/3 • 0,65 • 500 = 216,666  dus ongeveer 217 mensen
1/3 van de angsthazen is  1/3 • 0,35 • 500 = 58 mensen.
samen zijn dat  217 + 58 = 275 mensen.
5. De 35 angsthazen krassen in ieder geval elk één hokje open.
Dus van de 65 waaghalzen moeten er meer dan 25 één hokje openkrassen.
De kans dat een waaghals één hokje openkrast = P(MIN) = 1/3.
P(X > 25) = 1 - P(X ≤ 25) = 1 - BINOMCDF(65,1/3,25) ≈ 1 - 0,843 = 0,156
6. 1/4 = 1 + sin2(1/6π) + cos(1/6πn)
 ⇒  0,25 = 1 + 0,25 + cos(1/6πn)  Þ  -1 = cos(1/6πn)
 ⇒  1/6πn  = π  mod(2π)
 ⇒  n = 6  mod(12)
Tussen 0 en 50 geeft dat de oplossingen n = 6 , 18 , 30  en  42 
7. formulekaart:  cos 2x = 1 - 2 sin2x
substitueren geeft:
1,5 - 0,5 • cos2x + cos4x = 1,5 - 0,5 • (1 - 2sin2x) + cos 4x = 1,5 - 0,5 + sin2x + cos 4x
= 1 + sin2x + cos 4x  =  f4(x) 
8. Oppervlakte onder f4 is:

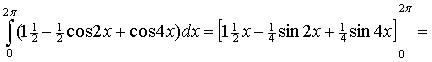
= (3π - 0 + 0) - (0) = 3π
De gehele rechthoek heeft oppervlakte 3 • 2π = 6π  dus de oppervlakte onder f4 is inderdaad de helft.
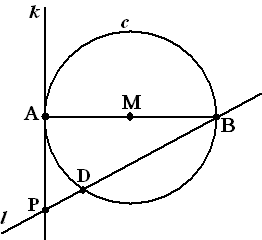
9. Als de cirkels elkaar raken in A moet het andere middelpunt op de lijn MA liggen.

Verder is de afstand van het middelpunt tot lijn l gelijk aan de afstand van dat middelpunt tot A (beiden is de straal van de nieuwe cirkel)

dat geeft zoiets:

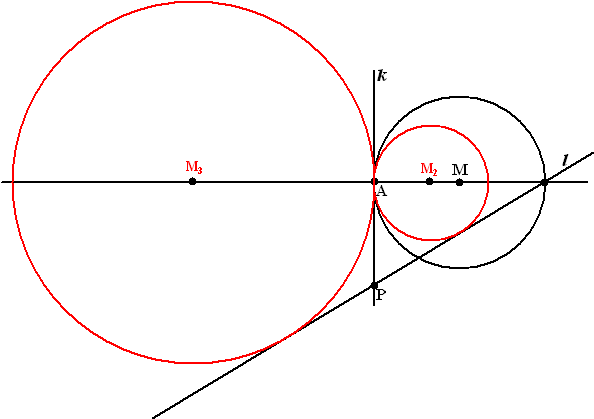
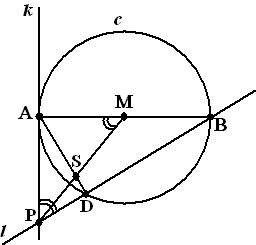
10. Omdat D op de cirkel ligt is ∠BDA = 90º (Thales; AB is een middellijn)
Noem ∠DBA = x  en  ∠DAB = y,  dan is  x + y = 90º   (hoekensom driehoek BAD)
maar dan is ∠DAP = x want samen met ∠DAB is het 90º
dan is ∠DPA = y  (hoekensom driehoek DPA)
dan is ∠PMA ook gelijk aan y  (gegeven)
omdat  ∠PMA en ∠DAM gelijk zijn is driehoek ASM gelijkbenig dus is AS = SM

als ∠AMP gelijk is aan y dan is ∠APM gelijk aan x  (hoekensom driehoek APM)
omdat ∠APM en ∠DAP gelijk zijn is driehoek ASP gelijkbenig en dus is AS = PS
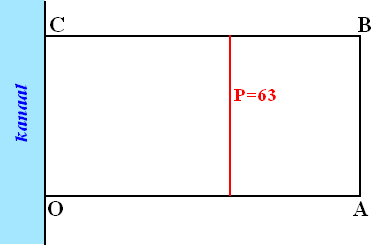
11. P = 55  ⇒  55 = 100 • 0,998x  ⇒  0,998x = 0,55  ⇒  x = log(0,55)/log(0,998) = 298,619...
P = 63  geeft op dezelfde manier x = 230,786...
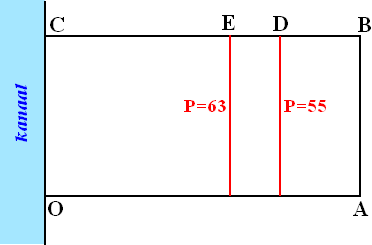
De lijn P = 55 is hieronder zó getekend dat  CD/CE = 298,619/230,786
Ofwel  CD ≈ 1,29 • CE

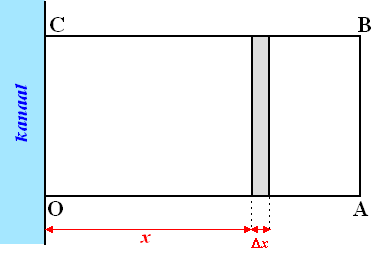
12. De oppervlakte van één zo'n rechthoekje is 5 • 200 = 1000 m2
Op afstand x van het kanaal kost zo'n rechthoekje dan 1000 • P(x)
Er zijn 80 zulke rechthoekjes te maken.
De totale grondprijs wordt dan  1000 • (P(0) + P(5) + P(10) + ... + P(395))
= 1000 • (100 • 0,9980 + 100 • 0,9985 + 100 • 0,99810 + ... + 100 • 0,998395)
= 1000 • 100 • {0,9980 + 0,9980 • 0,9985 + 0,9980 • (0,9985)2 + ... + 0,9980 • (0,9985)79}
Tussen accolades staat een meetkundige rij met beginwaarde 1 en reden r = 0,9985
De som S van de eerste 80 termen daarvan is 

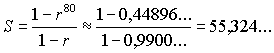
De totale prijs wordt dan 1000 • 100 • 55,324 ≈ 5,53 miljoen euro.
13.

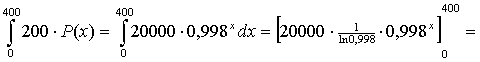
» (-4485200 + 9989997) = 5504797  ofwel ongeveer 5,50 miljoen euro.
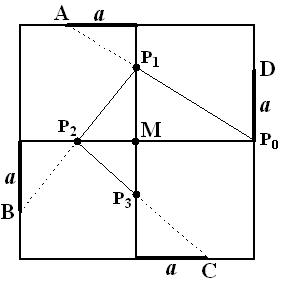
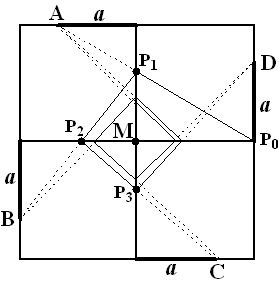
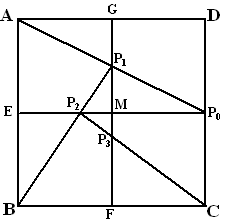
14. P0P1M is gelijkvormig met P0AE
dus u1 = MP1 = AE • MP0/EP0 = 1 • 1/2 = 0,5

MP1P2 is gelijkvormig met FP1B
dus u2 = MP2 = BF • MP1/FP1 = 1 • 0,5/1,5 = 1/3

MP2P3 is gelijkvormig met P0P2C
dus u3 = MP3 = P0C • MP2/P0P2 = 1 • 1/3/ 4/3 = 1/4

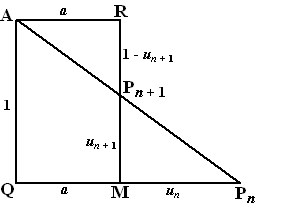
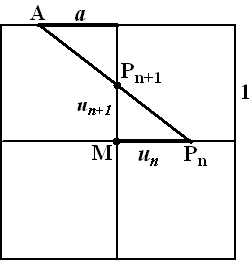
15. PnQA  is gelijkvormig met PnMPn+1

dus

vermenigvuldig met un en klaar.

16. voor het vierkant geldt  un+1 = un
gebruik de formule van de vorige vraag.
dat geeft  un = un/(un + a)
ofwel:  un + a = 1  ⇒  un = 1 - a = 1 - 2/3 = 1/3
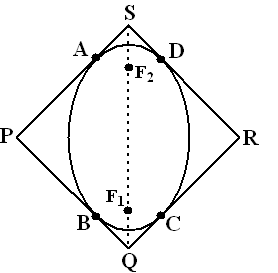
17. uit de raaklijneigenschap van ellipsen weet je dat ∠PAF1 = ∠SAF2
de figuur is symmetrisch in de lijn PR en als je hoek ∠BF1 daarin spiegelt krijg je ∠SAF2
dus geldt  ∠QBF1 = ∠SAF2 = ∠PAF1
18. ∠QBF1 + ∠PBF1 = 180º
∠QBF1 = ∠PAF1  (vraag 17)
dus ∠PAF1 + ∠PBF1 = 180º
dat zijn twee overstaande hoeken van de vierhoek dus is de vierhoek een koordenvierhoek.