VWO WB12,   2002 - II
Oppervlakte
Gegeven is de functie:  f(x) = √(x - 1)

De lijn k raakt de grafiek van f in het punt P(10,3). Zie de figuur hieronder.
5p 1. Stel met behulp van differentiëren een vergelijking op van k.
De grafiek van f, de lijn k en de x-as sluiten een vlakdeel in.
7p 2. Bereken exact de oppervlakte van dit vlakdeel.

 

 

Verdeling
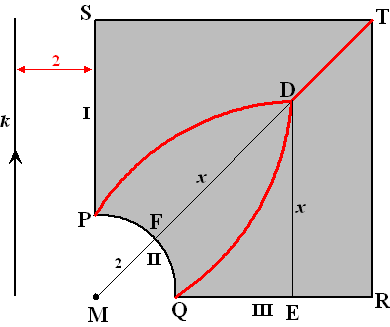
Het grijze gebied in de figuur hieronder is een deel van het vierkant MRTS met zijde 7. De grens PQ is een kwartcirkel met middelpunt M en straal 2. Er zijn drie landen, I, II en III, die alle drie aan het grijs gekleurde gebied grenzen. De grenzen met die landen zijn respectievelijk SP, PQ en QR.
Het grijze gebied wordt onder de drie landen verdeeld volgens het naaste-buur-principe.

In het grijze gebied ligt op de lijn MT een punt P dat even ver van de drie landen ligt.
3p

3.

 Bereken de afstand van D tot de drie landen in twee decimalen nauwkeurig.

 
7p

4.

 Teken in de figuur de conflictlijnen tussen de drie landen in het grijze gebied. Licht je werkwijze toe.

 
Een Lissajous-figuur
De bewegingsvergelijkingen:



(met 0 ≤ t ≤ 2π) beschrijven de baan van een bewegend punt. Deze baan heeft precies vier punten met de y-as gemeen.
4p 5. Bereken de coördinaten van deze punten.
Tijdens de beweging verandert de snelheid van het punt voortdurend. De hoogste snelheid die het punt kan bereiken wordt enkele malen bereikt. Als je de beweging op de GR simuleert lijkt het alsof deze hoogste waarde bereikt wordt bij het passeren van de y-as.
8p 6. Toon aan dat dit niet het geval is.

 
Schone-grond-verklaring
Om te mogen bouwen op een perceel grond is een zogeheten schone-grond-verklaring nodig.
Een onafhankelijke instantie neemt twee grondmonsters van zo'n perceel. Van elk perceel wordt in een laboratorium één monster getest op verontreiniging. Als er geen verontreiniging wordt aangetroffen wordt een schone-grond-verklaring afgegeven voor het betreffende perceel.

Ga in deze opgave uit van de volgende veronderstellingen:
Als de grond van een perceel verontreinigd is, wordt die verontreiniging in elk monster van dat perceel aangetroffen.
De kans dat een perceel verontreinigd is is 1%.
De kansen op verontreiniging voor verschillende percelen zijn onafhankelijk van elkaar.

Het testen van een monster is een kostbare zaak. In plaats van het afzonderlijk testen van de grond van elk perceel worden - om kosten te besparen - de grondmonsters van meerdere percelen bij elkaar gevoegd en als één geheel getest.

Veronderstel dat men grondmonsters van vijf percelen bij elkaar neemt en dit mengsel test. Als er geen verontreiniging in dit mengsel wordt aangetroffen, wordt voor elk van de betreffende percelen een schone-grond-verklaring afgegeven. Als er wel verontreiniging wordt aangetroffen test men van elk van de vijf percelen het tweede monster apart.
3p 7. Bewijs dat de kans dat men de tweede monsters zal moeten testen, afgerond op drie decimalen, gelijk is aan 0,049

 
Het nemen van twee grondmonsters van een perceel kost € 20,-. Een test in het laboratorium kost € 150,-.
6p 8. Toon aan dat de te verwachten kostenbesparing op het onderzoek van vijf percelen grond op deze manier € 563,25 is.

 
Uit de uitkomst van vraag 8 blijkt dat het inderdaad kostenbesparend is om een aantal monsters tegelijk te testen. Men vraagt zich af of een verdere kostenbesparing te realiseren is.
De grondmonsters van n percelen worden bij elkaar genomen.
5p 9. Bewijs dat de verwachtingswaarde van de kosten per perceel gelijk is aan :

170 + (150/n) - 150 • (0,99)n.

 
3p 10. Bereken bij welke waarde van n deze verwachtingswaarde minimaal is.

 

 

Aangeschreven cirkels.
Gegeven is een vierhoek ABCD met hoeken  a, b, g en d. De cirkel die raakt aan een zijde van de vierhoek en aan de verlengden van de twee aangrenzende zijden, noemen we een aangeschreven cirkel van de vierhoek. De middelpunten van de aangeschreven cirkels van vierhoek ABCD zijn M, N, O en P. Zie onderstaande figuur.

5p

11.

 Bewijs dat de punten M, B en N op één lijn liggen.

 
We weten nu dat A, B, C en D op de zijden van vierhoek MNOP liggen. Zie de figuur hieronder.

7p

12.

 Bewijs dat de punten M, N, O en P op één cirkel liggen.

 
Functies met een rij
Gegeven zijn de functies:
Voor elke waarde van k ≠ 0 heeft de grafiek van fk één top.
De top van de grafiek van f1 ligt op een kromme met vergelijking  y = 1/x
6p 13. Bewijs dat voor elke waarde van k ≠ 0 de top van de grafiek van fk op de kromme y = 1/x ligt.

 
De waarde van k wordt zodanig gekozen dat de grafiek van fk de lijn y = 1 snijdt in de punten A en B. De lengte van AB hangt af van de keuze van k.
6p 14. Wat is de kleinste gehele waarde van k waarvoor de lengte van AB groter is dan 2? Licht je antwoord toe.

 
In de rest van deze opgave werken we met de functie f3. Deze functie duiden we aan met de letter h,
dus  h(x) = ln3x/x
Zie de figuur hieronder voor de grafiek van h

De functie h heeft twee dekpunten a en b waarbij geldt  a < b.
4p

15.

 Benader a en b in drie decimalen nauwkeurig.

 
De rij u0,  u1, u2, u3, ... is gedefinieerd door  un+1 = h(un) met startwaarde u0.
5p 16. Teken in de figuur hierboven op de x-as alle startwaarden waarvoor de limiet van de rij gelijk is aan a. Licht je werkwijze toe.

 
UITWERKING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. f ' (x) = 0,5 • (x - 1)-0,5  dus  f '(10) = 0,5 • (9)-0,5 =  1/6 en dat is het hellinggetal van de raaklijn.
De raaklijn heeft dus vergelijking y = (1/6)•x + b
b kun je vinden door het raakpunt (10, 3) in te vullen:  3 = 10•(1/6) + b dus  b = 4/3
Daarmee is de vergelijking geworden  y = 1/6 • x + 11/3
2. Bereken de oppervlakte onder de rechte lijn en trek er daarna de oppervlakte onder de wortel vanaf.
y = 0  ⇒  1/6x + 11/3 = 0 ⇒  x = -8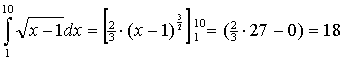 
 

De gevraagde oppervlakte is dus  het verschil tussen deze twee en is  9
3. Noem dat punt D.
Stel de afstand van D tot de drie gebieden gelijk aan x. Dan is dus DE = DF = x en D ligt op MT.
In driehoek DEM:
x2 + x2 = (x + 2)2
⇒  x2 - 4x - 4 = 0
⇒  x = 2 + 2Ö2 » 4,83
4. De conflictlijn van I en III is lijn MT.
De conflictlijn van I en II:
de afstand van een punt A tot SP is gelijk aan de afstand tot de cirkel, ofwel: d(A,SP) = d(A,cirkel)
tel bij beide afstanden 2 op:
d(A,SP) + 2 = d(A,M)
teken lijn k evenwijdig aan SP op afstand 2:
d(A,k) = d(A,M)
Dus liggen de punten A op een parabool met richtlijn k en brandpunt M.
Dat geeft deel PD, en door te spiegelen ook QD.
5. y-as wil zeggen x = 0  dus  cos3t = 0
Þ 3t = 0,5p (+ k • 2p)  of  3t = 1,5p (+ k • 2p)
Þ t = 1/6p (+ k • 2/3p)  of  t = 0,5p (+ k • 2/3p)
Tussen 0 en 2p geeft dat de oplossingen t =  1/6p  ,  1/2p  ,  5/6p ,  7/6p   ,  3/2p  ,  11/6p
De bijbehorende y-waarden zijn respectievelijk:  1/2  ,  1  ,  1/2  ,  -1/2  ,  -1  ,  -1/2
De gevraagde punten zijn dus  (0 , 1/2) en (0, 1)  en  (0,-1/2)  en  (0, -1)
6. x' = -3•sin3t  en  y' = cost
snelheid = v = Ö(x'2 + y '2)=Ö(9sin23t + cos2t)
voer in Y1 = Ö(9sin23t + cos2t) en bereken met CALC-Maximum de maximale snelheid.
Tussen 0 en 2p geeft dat  X = 0,5182... en  1,5707.... en  2,6233... en  3,6598... en  4,7123... en  5,7649.....
Het passeren van de y-as was bij  t =  1/6p  ,  1/2p  ,  5/6p ,  7/6p   ,  3/2p  ,  11/6p (opgave 13)
Dat is resp. afgerond  0,5235... en  1,5707...  en  2,6179... en   3,66519... en  4,7123... en  5,7595...
en dat is niet hetzelfde.
7. P(tweede monsters moeten getest) = P(minstens één monster verontreinigd) = 1 - P(geen monster verontreinigd) = 1 - 0,995 = 1 - 0,95099.. = 0,0490099... = 0,049 (afgerond)
8. Bij apart meten kost het 5 • 150 = 750 euro.

In groepjes meten geeft kans 0,049 dat de tweede monsters getest moeten worden, en in dat geval zijn er 6 metingen gedaan dus zijn de totale kosten 6 • 150 = 900 euro.
De kans is 1 - 0,049 = 0,951 dat de tweede monsters niet getest hoeven te worden , in dat geval was er maar 1 meting nodig en zijn de koster 150 euro.
De gemiddelde kosten (verwachtingswaarde) zijn dus  900 • 0,049 + 150 • 0.951 = 186,75 euro.

Dat is een besparing van 750 - 186,75 = 563,25 euro.
9. Groepjes van n geeft kans  0,99n dat er maar één meting nodig is (alles schoon) en dus kans  1 - 0,99n dat alle tweede monsters gemeten moeten worden. In dat geval zijn er n + 1 metingen nodig.
Het gemiddelde aantal metingen voor n monsters is dus 
0,99n • 1 + (1 - 0,99n)•(n + 1) = 0.99n + n  + 1 - n • 0,99n - 0,99n = n + 1 - n • 0,99n
Per monster is dat (delen door n):  1 + (1/n) - 0,99n  metingen
De kosten zijn per meting 150 euro, dus totaal wordt dat  150 + 150/n - 150•0,99n  en daar komt nog 20 euro voor het nemen van de grondmonsters bij.
Samen in totaal 170 + 150/n - 150 • 0,99n
10. Voer in:  Y1 = 170 + 150/n - 150 • 0,99n  en kijk in de tabel.
Dat geeft een minimum bij n = 11 van 49,3356..... euro
11. M ligt even ver van BA als van BC dus is MB bissectrice van de hoek bij B.
Op dezelfde manier is BN ook bissectrice van de hoek bij B.
Omdat de hoeken overstaande hoeken zijn, zijn ze gelijk.
Dus ÐMBA + ÐABC + ÐCBN =  ÐMBA + ÐABC + ÐMBA = 2•ÐMBA + ÐABC = 180º
Dus is MBN een rechte lijn.
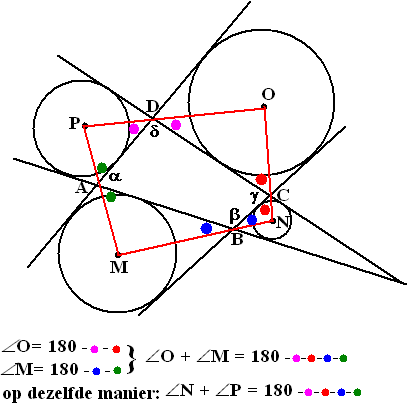12. Vanwege de bissectrices (zie vraag 11) zijn de gekleurde hoeken hiernaast even groot.

Onder de figuur wordt bewezen dat ÐO + ÐM = ÐN + ÐP
Omdat de vier hoeken van een vierhoek samen 360º zijn, zijn beide koppels dus gelijk aan 180º.
Maar dan is MNOP een koordenvierhoek, dus liggen de vierhoekpunten op één cirkel.

q.e.d.
13.
f '(x) = 0 geeft  1 - ln kx = 0  ⇒ ln kx = 1 ⇒ kx = e  ⇒ x = e/k
Dan is  y = ln(k • e/k )  / x =  lne / x =   1/x
14.
Hiernaast zie je een grafiekenbundel van  y = ln(kx)/x voor k = 1, 2, 3, 4, 5   en de lijn y = 1.
Makkelijk in te toetsen in de GR als  Y1 = ln({0,1,2,3,4,5}X)/X met gebruik van de "dikke komma" tussen de k-waarden.
Het lijkt erop dat bij de zwarte grafiek de lengte van AB voor het eerst groter is dan 2.

Controle met  Y1 = ln(5x)/x en Y2 = 1 en INTERSECT geeft de punten (0.259.. , 1)  en  (2.543... , 1)  en de afstand daartussen is inderdaad meer dan 2.

Hetzelfde met Y1 = ln(4x)/x
geeft de punten (0.357.. , 1) en  (2.153... , 1) en de afstand daartussen is kleiner dan 2.

Dus voor k = 5 is de afstand AB voor het eerst groter dan 2.
15. Dekpunten zijn snijpunten met y = x
ln(3x)/ x = x  invoeren in de GR, en dan intersect levert x » 0,387  of  x » 1,087
dus a = 0,387 en b = 1,087
16. De limiet van een rij zal nooit a worden, maar altijd naar b gaan of divergeren.
De enige uitzonderingen zijn de punten waarvoor de beginwaarde al gelijk is aan a
Dat zijn de snijpunten van de lijn y = a met de grafiek.
Die staan bij de blauwe pijlen hiernaast
(x = 0,387 en x = 8,310)