VWO WB1, 2006 - I

 

Sauna.
Om 15.00 uur wordt het verwarmingselement van een sauna aangezet. Vanaf dat moment wordt de sauna opgewarmd. Dan geldt:  S(t) = 200 - 180 • e-0,29t
Hierin is S de temperatuur in de sauna in graden Celsius en t de tijd in uren vanaf 15.00 uur.

De thermostaat van de sauna is ingesteld op 100ºC. Zodra die temperatuur bereikt is, wordt het opwarmen gestopt. Vanaf dat moment wordt de temperatuur constant gehouden. In onderstaande figuur staat de grafiek van  S.

4p

1.

 Bereken hoe laat het opwarmen wordt gestopt. Geef het tijdstip in minuten nauwkeurig.
 
4p

2.

 Bereken met behulp van differentiëren de snelheid waarmee de temperatuur in de sauna toeneemt om 16.00 uur. Geef je antwoord in tienden van graden Celsius per minuut.
 
Om bij een ingestelde temperatuur van de thermostaat uit te rekenen hoe lang de sauna nodig heeft om deze temperatuur te bereiken, kun je een formule gebruikten die t uitdrukt in S.
4p

3.

 Druk t uit in S.

 

 

Bosbouwprojecten
Wereldwijd bestaan bosbouwprojecten waarin geïnvesteerd kan worden. Er wordt elk jaar teakhout aangeplant dat na 20 jaar gekapt wordt. Om beleggers te interesseren wordt van verschillende projecten informatie gepubliceerd over de gemiddelde opbrengst in kubieke meter per hectare.

Bij European Trees is de gemiddelde opbrengst normaal verdeeld met verwachtingswaarde 800 m3/ha en standaardafwijking 33 m3/ha.
4p

4.

 Bereken de kans dat bij European Trees de gemiddelde opbrengst meer dan 10% afwijkt van de verwachtingswaarde van 800 m3/ha.

 
Bij Earthbound is de gemiddelde opbrengst ook normaal verdeeld. De verwachtingswaarde van de gemiddelde opbrengst is 950 m3/ha. De kans op een gemiddelde opbrengst van minder dan 98% van de verwachtingswaarde is slechts 0,01.
4p

5.

 Bereken de standaardafwijking van de gemiddelde opbrengst voor Earthbound.

 

 

Bedekken.
Een geodriehoek is een gelijkbenige rechthoekige driehoek. We plaatsen twee geodriehoeken met een lange zijde van 16 cm in een rechthoekig assenstelsel met eenheid 1 cm op de manier die in de figuur hieronder (verkleind) is getekend.
De top A van de linker driehoek heeft de coördinaten (0,8)
De top B van de rechter driehoek heeft de coördinaten (8,0).

De linker driehoek begint op tijdstip t = 0 naar rechts te schuiven over de rechter driehoek met een snelheid van 1 cm/s. Daarbij wordt een gedeelte van de rechter driehoek door de linker driehoek bedekt. De tijd t wordt gemeten in seconden.
In de figuur hieronder is de situatie voor een zeker tijdstip t getekend.
Punt A heeft dan de coördinaten (t, 8). Het bedekte gebied is grijs gekleurd.

De afstand in cm tussen A en B op tijdstip t noemen we a(t).
Er geldt:  a(t) = √(128 - 16t + t2)
3p

6.

 Toon dit aan.

 
Het bedekte gebied op een tijdstip t tussen 0 en 16 is een rechthoek. De oppervlakte in cm2 van deze rechthoek noemen we G(t). De zijden van de rechthoek zijn ook rechthoekszijden van gelijkbenige rechthoekige driehoeken met lange zijden t en 16 - t.

Er geldt:  G(t) = -1/2t2 + 8t
4p

7.

 Toon dit aan.

 
De oppervlakte G van het bedekte gebied neemt eerst toe en later af. De afstand a tussen A en B neemt eerst af en later toe.
5p

8.

 Leid met behulp van differentiëren uit de formules voor G(t) en a(t) af dat G en a op hetzelfde tijdstip hun uiterste waarde bereiken.

 
De oppervlakte G kan ook uitgedrukt worden in a.
Er geldt:  G = c - 1/2a2  waarbij  8 ≤ a ≤ √128
4p

9.

 Bereken c.

 

In een vierkant.
Van een vierkant OABC met zijde 4 ligt A op de positieve x-as en C op de positieve y-as.
Verder is gegeven de functie  f(x) = 1/x

De grafiek van f  snijdt de zijde AB van het vierkant in het punt P en de zijde BC in het punt Q. Zie de figuur hiernaast.
De raaklijn aan de grafiek van f in het punt met x-coördinaat 2 gaat door het punt A.

5p

10.

 Toon dit aan
De grafiek van f verdeelt het vierkant in twee stukken. Eén van die stukken is in onderstaande figuur grijs gekleurd; dat stuk noemen we V.

4p

11.

 Bereken de omtrek  van V in twee decimalen nauwkeurig.

 
4p

12.

 Toon aan dat de oppervlakte van V exact gelijk is aan 1 + 2ln4

 
Voor de zijde van het vierkant kan ook een andere waarde dan 4 gekozen worden. Noem de zijde a. Zie onderstaande figuur.

In deze figuur is a zodanig gekozen dat de lijn AC niet raakt aan de grafiek van f.  Er is één waarde van a waarvoor AC wel raakt aan de grafiek van f.
4p

13.

 Bereken deze waarde van a exact.

 
Knock-out-systeem
Een spelprogramma op televisie telt bij aanvang 16 deelnemers. Het spel wordt gespeeld in vier rondes. In elke ronde nemen de spelers het in een spelletje van één-tegen-één tegen elkaar op. Van elk tweetal gaat de winnaar door naar de volgende ronde; de verliezer doet niet meer mee. In elke ronde wordt het aantal deelnemers dus gehalveerd; men sprekkt van een knock-out-systeem.
De spelletjes zijn van zodanige aard dat de uitslag volledig bepaald wordt door het toeval. Bij elk spelletje hebben beide spelers dus kans 1/2 om te winnen.
Vooraf wordt een speelschema opgesteld; zie de volgende figuur.

Elke deelnemer krijgt door loting een nummer. Dit nummer is zijn plaats in het schema. Boven in het schema zie je wie tegen wie speelt in de eerste ronde. Na de eerste ronde zijn er nog acht spelers over. De winnaar van de spelers 1 en 2 speelt in de tweede ronde tegen de winnaar van de spelers 3 en 4, enzovoort. In de vierde ronde wordt de finale gespeeld door de twee overgebleven deelnemers.

Er nemen 8 mannen en 8 vrouwen aan het spelprogramma deel.
3p

14.

 Bereken de kans dat de nummers 1 tot en met 4 worden gegeven aan drie mannen en een vrouw.

 
4p

15.

 Bereken de kans dat speler 1 de finale speelt tegen speler 16 en speler 1 deze finale wint.

 
Elke deelnemer speelt 1, 2, 3 of 4 rondes.
4p

16.

 Bereken de verwachtingswaarde van het aantal rondes dat een deelnemer speelt.

 
In een jaar is het spelprogramma 52 keer op televisie geweest. Elke keer hebben er evenveel mannen als vrouwen meegedaan. Er is enige twijfel of elke deelnemer wel evenveel kans heeft om het spelprogramma te winnen. Misschien hebben vrouwen meer kans.
Daarom wordt het aantal keren geteld dat een vrouw het spelprogramma won. Daarna berekent men de kans op dat aantal of een hoger aantal, aangenomen dat alle deelnemers evenveel kans hebben om het spelprogramma te winnen. Het aantal wordt abnormaal hoog gevonden als deze kans kleiner is dan 5%.
5p

17.

 Bereken welke aantallen vrouwelijke winnaars abnormaal hoog worden gevonden.

 

 

Oppervlakte van een trapezium.
In de figuur hieronder staat een kwart van de eenheidscirkel met O(0,0), A(1,0) en B(0,1).
Op tijdstip t = 0 start een punt P in A en beweegt langs de cirkelboog AB; op tijdstip t heeft P de coördinaten (cos t, sin t). Q is de loodrechte projectie van P op de y-as.
We bekijken de oppervlakte V van het trapezium OAPQ op tijdstip t waarbij t in het interval  〈0, 1/2π〉 ligt.

De oppervlakte V van het trapezium is  1/2sin t + 1/4sin 2t
4p

18.

 Toon dit aan.

 
De waarde die V op tijdstip 1/4p heeft, wordt ook op een ander tijdstip aangenomen.
3p

19.

 Bereken dit andere tijdstip in twee decimalen nauwkeurig.

 
5p

20.

 Bereken met behulp van differentiëren voor welke waarde van t de oppervlakte V maximaal is.

 
De oppervlakte van het trapezium OAPQ verandert op het tijdsinterval 〈0, 1/2π〉  voortdurend. In de figuur hiernaast is de grafiek van V getekend als functie van t op dit tijdsinterval.
De gemiddelde oppervlakte van het trapezium OAPQ over het tijdsinterval 〈0, 1/2π〉  noemen we k. In de figuur hiernaast is de lijn y = k getekend.

Er geldt: de oppervlakte van het gebied dat wordt ingesloten door de grafiek van V, de t-as en de lijn t = 1/2π is gelijk aan de oppervlakte van het gebied dat wordt ingesloten door de horizontale lijn y = k, de t-as , de y-as en de lijn t = 1/2π.

6p

21.

 Bereken met behulp van integreren de exacte waarde van k.

 

 
OPLOSSING
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. 100 = 200 - 180 • e-0,29t  ⇒  -100 = -180 • e-0,29t  ⇒  e-0,29t = 100/180  ⇒  -0,29t = ln(100/180) » -0,588
 ⇒  t = -0,588/-0,29 ≈ 2,0268 uren en dat is  2,0268 • 60 = 121,6 minuten
Dus ongeveer 2 minuten over 5  (17:02) wordt het opwarmen gestopt.
2. S'(t) = -180 • e-0,29t • -0,29 = 52,2 • e-0,29t
S'(1) = 39,059 ºC/uur en dat is 0,65 ºC/minuut dus ongeveer 0,7 ºC/minuut.
3. S - 200 = -180 • e-0,29t  Þ  (S - 200)/-180 = e-0,29t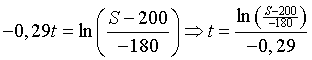
4. Minder dan 10% afwijking is tussen  720 en 880, en de kans daarop is
normalcdf(720, 880, 800, 33) ≈ 0,9847  dus de kans op minstens 10% afwijking is 1 - 0,9847 ≈ 0,015
5. 98% van 950 is 931
normalcdf(0, 931, 950, X) = 0,01
Y1 = normalcdf(0, 931, 950, X) en Y2 = 0,01
window bijv. Xmin = 0,   Xmax = 20, Ymin = 0,  Ymax = 0,02
intersect levert  X ≈ 8,17
6. A(t,8) en B(8,0) dus Pythagoras geeft:  AB = √((t - 8)2 + 82 ) = √(t2 - 16t + 64 + 64) = √(t2 - 16t + 128)
7. Een gelijkbenige driehoek met lange zijde t heeft rechthoekszijden 1/2√2 • t
Een gelijkbenige driehoek met lange zijde 16 - t heeft rechthoekszijden 1/2√2 • (16 - t)
De oppervlakte is dus 1/2√2 • t • 1/2√2 • (16 - t) = 1/4 • 2 • (16t - t2) = 8t - 1/2t2 
8. G'(t) = -t + 8 en dat is nul als t = 8

a'(t) = 1/2(128 - 16t + t2 )-1/2 • (-16 + 2t) en dat is nul als -16 + 2t = 0  ofwel als t = 8.

Dat is dus tegelijk.
9. c - 1/2a2 = c - 1/2(128 - 16t + t2 ) = c - 64 + 8t - 1/2t2 =  (c - 64) + G
Dat is gelijk aan G als c - 64 = 0  ⇒  c = 64
10. f '(x) = -1 • x-2  dus  f '(2) = -1/4
De raaklijn is dus  y = -1/4x + b en moet door het punt (2, 1/2) gaan.
Dus 1/2 = -1/4 • 2 + b  ⇒  b = 1
De raaklijn is dus  y = -1/4 x + 1
11. Voor de lengte L van het deel van de grafiek tussen P en Q geldt: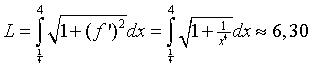

De totale omtrek OAPQC wordt dan  4 + 1/4 + 6,30 + 1/4 + 4 ≈ 14,80
12. Voor de oppervlakte onder de grafiek van f tussen x = 1/4 en x = 4 geldt: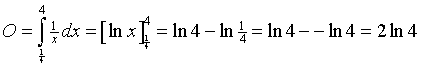

Daar moet nog een rechthoek van 1/4 bij 4 bij opgeteld worden, zodat de totale oppervlakte gelijk wordt aan 1/4 • 4 + 2 ln4 = 1 + 2ln4.
13. De helling van AC is -1, dus moet de afgeleide van f ook -1 zijn.
-x-2 = -1  ⇒  x = 1  (dat hadden we ook uit symmetrieoverwegingen wel kunnen raden trouwens)
De lijn y = -x + a  moet dus door (1,1) gaan, dus 1 = -1 + a ⇒ a = 2
14. P(MMMV) = 8/16 • 7/15 • 6/14 • 8/13 = 4/65
Er zijn  4 nCr 1 = 4  zulke mogelijke volgorden, dus de totale kans is 4 • 4/65 = 16/65
15. Dan moet speler 1 vier wedstrijden winnen: kans (1/2)4 = 1/16
verder moet speler 2 de eerste drie wedstrijden winnen: kans (1/2)3 = 1/8
Samen geeft dat een kans van  1/16 • 1/8 = 1/128
16.
aantal wedstrijden 1 2 3 4
kans 1/2 1/2 • 1/2 = 1/4 1/2 • 1/2 • 1/2 = 1/8 1/2 • 1/2 • 1/2 = 1/8
De verwachtingswaarde is dan  1 • 1/2 + 2 • 1/4 + 3• 1/8 + 4 • 1/8 = 1,875

of:
Er worden 8 + 4 + 2 + 1 = 15 wedstrijden gespeeld, dus wordt 30 keer door iemand een wedstrijd gespeeld.
Er zijn 16 deelnemers, dus gemiddeld is dat 30/16 = 1,875 wedstrijden per persoon.

17. Stel V het aantal vrouwen dat wint, en g het grensgetal waarnaar we opzoek zijn;
P(V ≥ g , n = 52, p = 1/2) < 0,05
1 - P(V ≤ g - 1) < 0,05
Voer dus in Y1 = 1 - binomcdf(52, 0.5, X - 1) en kijk met TABLE wanneer de waarde voor het eerst kleiner is dan 0,05. Dat is bij X = 33 (P = 0,0352)
Dus 33 of meer vrouwelijke winnaars wordt abnormaal hoog gevonden.
18. Noem P' de projectie van P op de x-as.
Rechthoek OP'PQ heeft oppervlakte cos t • sin t
Driehoek PP'A heeft oppervlakte  1/2•(1 - cos t) • sint
Samen is dat   cost • sin t + 1/2•(1 - cost) • sint = cost sint + 1/2sint - 1/2cost • sint =
= 1/2sint +  1/2cost • sint = 1/2sint +  1/4 (2cost • sint) = 1/2sint + 1/4sin2t
19. V(1/4 p) = 1/2sin1/4 p + 1/4 sin1/2p = 1/4 √2 + 1/4
Y1 =  1/4 √2 + 1/4 en  Y2 = 1/2sin X + 1/4sin 2X
window bijv.  Xmin = 0,   Xmax = 1/2 p, Ymin = 0,  Ymax =1
intersect levert X ≈ 1,32
20. V' = 1/2cos t + 2 • 1/4 cos(2t) = 1/2cos t +  1/2cos 2t
V' = 0  ⇒  cos t + cos 2t = 0 
⇒  cos t = -cos 2t = cos(π -2t)
 ⇒  t = π - 2t  ∨   t = 2π - (π - 2t)
 ⇒ t = π/3 
21. Voor de oppervlakte onder de grafiek van V geldt: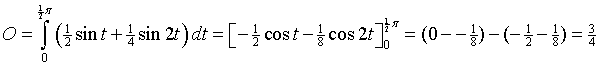

De oppervlakte onder de lijn y = k is  1/2π • k
1/2π • k  = 3/4  ⇒  k = 3/2π