| Spreekuur | |||
| Een huisarts heeft op elke werkdag twee uren
gereserveerd voor een spreekuur. De ervaring heeft haar geleerd dat zij
tijdens het spreekuur gemiddeld tien minuten voor een patiŽnt nodig
heeft. De huisarts deelt de patiŽnten die van haar spreekuur gebruik maken in drie groepen in: |
|||
|
|||
| We maken bij deze situatie het volgende wiskundige model: | |||
|
|||
| 4p | 4. | Bereken de verwachtingswaarde van het aantal tijdrovende patiŽnten tijdens een spreekuur in twee decimalen nauwkeurig. | |
| 5p | 5. | Bereken in twee decimalen nauwkeurig de kans dat de huisarts tijdens een spreekuur 2 gemakkelijke en 10 gewone patiŽnten krijgt. | |
| 5p | 6. | Bereken in twee decimalen nauwkeurig de kans dat tijdens een spreekuur minstens zes patiŽnten meer dan 10 minuten kosten. | |
| Neem aan dat de totale tijd die
de arts voor 60 patiŽnten nodig heeft normaal verdeeld is met een
gemiddelde van 600 minuten en een standaardafwijking van 4÷60
minuten. In een week voor de 60 patiŽnten op haar spreekuur in totaal 654 minuten nodig. Dat is aanzienlijk meer dan de 600 minuten die je zou verwachten. |
|||
| 5p | 7. | Onderzoek of deze gegevens voldoende aanleiding geven om de veronderstelde gemiddelde tijd van 10 minuten te verhogen, bij een significantieniveau van 5%. | |
| De huisarts beweert dat zij de afgelopen 5
jaar van haar ruim 3000 patiŽnten 30% wel eens een keer doorverwezen
heeft naar een specialist in het ziekenhuis. Haar plaatsvervanger (tijdens een vakantie) denkt dat dit percentage minder is en neemt een steekproef van 50 patiŽnten. |
|||
| 4p | 8. | Bereken de kans dat de plaatsvervanger in deze steekproef minder dan 10 doorverwezen patiŽnten vindt, als de huisarts gelijk heeft. | |
| Voedselbehoefte | |||
| In een zeker gebied wordt een grote
toename van de bevolking voorzien. Om de daarmee gepaard gaande
problemen het hoofd te kunnen bieden, heeft men een schatting nodig van
de grootte van de bevolking voor de komende jaren. Daarvoor stelt men
het volgende model op voor de grootte van de bevolking: B(t)
= 228 ē e0,1t Hierin is B het aantal mensen in duizenden en t de tijd in jaren. Het komende jaar loopt van t = 0 tot t = 1. In deze opgave werken we met jaren van 360 dagen en maanden van 30 dagen. |
|||
| 4p | 9. | Bereken de procentuele toename van de bevolking per maand. | |
| Voedseldeskundigen hanteren
als vuistregel: per persoon is er per dag
0,4 kg vast voedsel nodig. De totale benodigde hoeveelheid vast voedsel voor de inwoners van het gebied in het komende jaar noemen we V (in kg). Iemand wil berekenen hoe groot V is. Hij gebruikt daartoe eerst een benaderingsmethode. Hij bepaalt het gemiddelde van de groottes van de bevolking op t = 0 en t = 1. Hij gaat er vanuit dat de bevolkingsomvang het gehele jaar gelijk is aan dit gemiddelde. |
|||
| 3p | 10. | Bereken V volgens deze methode. | |
| Een nauwkeuriger schatting van V kan verkregen worden door voor iedere dag van het jaar de voedselbehoefte te berekenen en deze voedselbehoeften op te tellen. | |||
| 5p | 11. | Bereken V volgens deze tweede methode. | |
| Een derde methode om V te berekenen is met behulp van een integraal. | |||
| 4p | 12. | Bereken V met behulp van primitiveren volgens deze derde methode. | |
| De wijzers van een uurwerk | |||
| We volgen de eindpunten van
de wijzers van een uurwerk. Daartoe brengen we een assenstelsel aan met
de oorsprong in het draaipunt van de wijzers, de positieve x-as
door "drie uur", de positieve y-as door "12
uur" en met de cm als eenheid. We rekenen de tijd t in uren,
vanaf 0:00 uur.
De bewegingsvergelijkingen van het eindpunt van de grote wijzer
zijn: |
|||
| 5p | 13. | Teken in ťťn figuur op ware grootte de banen van de eindpunten van de wijzers en geef daarin de wijzers aan op het tijdstip t = 1,3. Licht je werkwijze toe. | |
| Op het tijdstip t = 0 liggen de wijzers over elkaar heen. | |||
| 4p | 14. | Bereken het eerste tijdstip na t = 0 waarop dit weer het geval is. | |
| De (rechtstreekse) afstand tussen de eindpunten van de wijzers verandert voortdurend. | |||
| 6p | 15. | Toon aan dat deze afstand op tijdstip t gelijk is aan: |
|
| 4p | 16. | Bereken het eerste tijdstip na t = 0 waarop de eindpunten van de wijzers, samen met de oorsprong, een gelijkbenige driehoek vormen. | |
| Twee halve parabolen | |||
| Gegeven zijn de functies: f(x) = x2 en g(x) = √x, beide met domein [0,→〉. Zie de volgende figuur. | |||
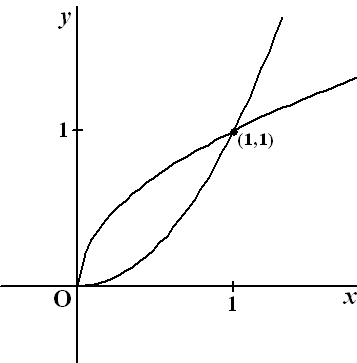 |
|||
| De lijn x = p, met 0 < p < 1, snijdt de grafiek van f in A en de grafiek van g in B. | |||
| 7p | 17. | Bereken de exacte waarde van p waarvoor de lengte van het lijnstuk AB maximaal is. | |
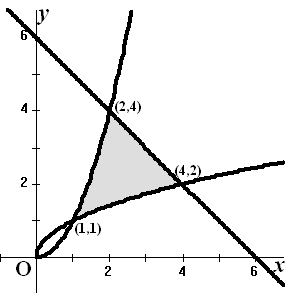
| In de figuur hieronder zijn
de grafieken van f en g en ook de lijn y
= 6 - x getekend. Het gebied, ingesloten door de grafiek van f, de grafiek van g, en de lijn y = 6 - x, is in de figuur grijs gekleurd. |
|||
 |
|||
| 7p | 18. | Bereken algebraÔsch de exacte oppervlakte van dit gebied. | |
| OPLOSSINGEN | |
| Het officiŽle (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten. | |
| 1. | Stroomopwaarts is de
snelheid 20 - 8 = 12 km/u, dus dat duurt 42/12 =
3,5 uur. Stroomafwaarts duurt de tocht 42/28 = 1,5 uur. Samen is dat 5 uur. |
| 2. | Ten opzichte van de
wal is de snelheid v - 8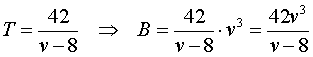
|
| 3. |
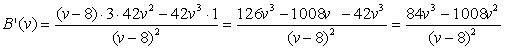
B'= 0 ⇒ 84v3 - 1008v2 = 0 ⇒ v2 ē (84v - 1008) = 0 ⇒ v = 0 ∨ v = 1008/84 = 12 Het minimum van B is bij v = 12 |
| 4. | De kans op een
tijdrovende patiŽnt is normalcdf(15,1E99,10,4) = 0,1056 De verwachtingswaarde is dan 12 ē 0,1056 = 1,27 tijdrovende patiŽnten per spreekuur |
| 5. | P(makkelijke) =
P(tijdrovende) = 0,1056 (zie vraag 4) P(gewone) = 1 - 0,1056 - 0,1056 = 0,7887 (of normalcdf(5,15,10,4)) P(2 makkelijk en 10 gewoon) = 0,10562 ē 0,788710 ē 12 nCr 2 = 0,07 |
| 6. | P(meer dan 120
minuten) = 0,5. Het aantal is binomiaal verdeeld met n = 12 en p = 0,5 P(X ≥ 6) = 1 - P(X ≤ 5) = 1 - binomcdf(12 , 0.5 , 5) = 1 - 0,387 = 0,61 |
| 7. | H0: het
gemiddelde is 10 (de huisarts). Voor 60 patiŽnten wordt dit Ķ =
600 met s = 4√60 H1: het gemiddelde is meer dan 10 eenzijdige toets met α = 0,05 overschrijdingskans is P(X > 654) = normalcdf(654, 1E99 , 600 , 4√60) = 0,4068... Dat is kleiner dan α dus moet H0 verworpen worden Er is dus WEL voldoende aanleiding om het gemiddelde te verhogen. |
| 8. | Het aantal
doorverwezen patiŽnten X is binomiaal verdeeld met n = 50 en p
= 0,30 P(X < 10) = P(X ≤ 9) = binomcdf(50, 0.3 , 9) = 0,04023... |
| 9. | De groeifactor per
jaar is e0,1 dus per maand (e0,1)1/12
= 1,00836... Dat is dus ongeveer 0,84% |
| 10. | B(0) = 228 dus dat
zijn 228000 mensen B(1) = 228 ē e0,1 = 251.9789.. dus dat zijn 251979 mensen Gemiddelde is (228000 + 251979)/2 = 239989,5 en omdat hij ervan uit gaat dat de bevolking hier het hele jaar aan gelijk is, moet dat in hele mensen worden 239990 V = 0,4 ē 360 ē 239990 = 34558560 kg. |
| 11. | Op dag 1: V =
0,4 ē 228 ē e0,1 ē 1/360 Op dag 2: V = 0,4 ē 228 ē e0,1ē2/360 enz. Alles optellen geeft V = 0,4 ē 228 ē (e0,1 ē 1/360 + e0,1ē2/360 + e0,1ē3/360 + ... + e0,1ē360/360 ) Tussen haakjes staat een meetkundige rij met reden e1/360 De som van deze 360 termen wordt dan : 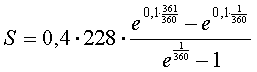
Daar komt uit (vermenigvuldig met 1000 omdat B in duizendtallen is): V = 0,4 ē 228 ē 1000 ē 37,8194... = 3449136 kg |
| 12. |
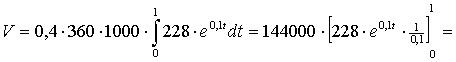
= 144000 ē (2519,789... - 2280) = 34529716 kg |
| 13. | De banen zijn twee
cirkels met middelpunt oorsprong en stralen 3 en 2. Grote wijzer: x(1,3) = 2,85 en y(1,3) = -0,93 Kleine wijzer: x(1,3) = 1,26 en y(1,3) = 1,55 Dat geeft deze tekening: 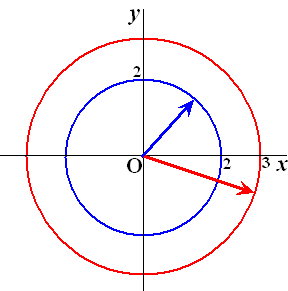 |
| 14. | Als de wijzers over
elkaar liggen moeten de x-coŲrdinaten ťn de y-coŲrdinaten
van hun uiteinden gelijk zijn. cos 2πt = cos 1/6πt ⇒ 2πt = 1/6πt (mod 2π) ∨ 2πt = 2π - 1/6πt (mod 2π) ⇒ 15/6πt = 0 (mod 2π) ∨ 1/6πt = 0 (mod 2π) ⇒ t = 0 (mod 12/11) ∨ t = 0 (mod 12) Dat geeft de rij oplossingen: 0 , 12/11 , 24/11 , 36/11 , ..... sin 2πt =
sin 1/6πt
|
| 15. |
Maar omdat cos2x + sin2x = 1 vereenvoudigt dit tot: Het deel tussen haakjes onder de wortel staat op de formulekaart: sinasinb + cosacosb = cos(a-b), dus: en dat is inderdaad de gezochte formule. |
| 16. | Als de wijzers voor
't eerst een gelijkbenige driehoek vormen, dan moet de afstand tussen de
uiteinden van de wijzers gelijk zijn aan de lengte van de kleine wijzer,
in dit geval 2. Dus 13 - 12cos11/6π t = 4 ⇒ 12 cos 11/6πt = 9 ⇒ cos 11/6πt = 0,75 ⇒ 11/6πt = 0,7227 (mod 2π) ∨ 11/6πt = 2π - 0,7227 = 5,5605 (mod 2π) ⇒ t = 0,125 (mod 1,09) ∨ t = 0,965 (mod 1,09) (maar oplossen met de GR mag natuurlijk ook....) De kleinste oplossing is t = 0,125 |
| 17. | De lengte van AB is
L = yg - yf =
√x
- x2 Dat is maximaal als de afgeleide nul is. L' = 0,5 ē x-0,5 - 2x 0,5 ē x-0,5 - 2x = 0 ⇒ 0,5x-0,5 = 2x ⇒ 0,5 = 2x1,5 ⇒ x1,5 = 0,25 ⇒ x = 0,251/1,5 = 0,252/3 |
| 18. | Verdeel het gebied
in twee stukken. gebied I: tussen x = 1 en x = 2 Daar ligt f boven g 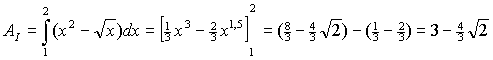
gebied
II : tussen x = 2 en x = 4. Daar ligt 6 - x
boven g Totale oppervlakte is dan 3 - 4/3√2 + 2/3 + 4/3√2 = 32/3 |