VWO WB1,  2002 - II
Cesuur bij examens
Bij de eindexamens in de jaren 1997 tot en met 2000 werden aan enkele VWO-scholen experimentele examens afgenomen in het vak Wiskunde-B. Bij deze examens waren elk jaar maximaal 90 punten te behalen.
Na afname van een examen bepaalt een overheidsinstelling de grens tussen onvoldoende en voldoende, de zogeheten cesuur. Cesuur 44/45 betekent dat kandidaten met een score van 45 of meer punten een voldoende krijgen en kandidaten met een score van 44 of minder punten een onvoldoende.

Bij het experimentele examen in 1997 waren de scores bij benadering normaal verdeeld met gemiddelde 52,0 en standaardafwijking 16,0. De Cesuur was  44/45. De grens tussen voldoende en onvoldoende lag dus bij 44,5 punten. De vragen 1 en 2 hebben betrekking op het experimentele examen in 1997.
3p 1. Bereken het percentage onvoldoendes.

 
Er zijn onderwijsdeskundigen die van mening zijn dat het percentage onvoldoendes bij een examen 25% zou moeten zijn.
3p 2. Bereken bij welke cesuur het percentage onvoldoendes het dichtst bij 25% ligt.

 
De tabel hieronder bevat de cumulatieve frequenties van alle scores bij het experimentele examen in 2000. In deze tabel is onder andere af te lezen dat bij een cesuur van 44/45 het aantal onvoldoendes 104 zou bedragen.
score freq. cum.
freq.		   score freq. cum.
freq.		   score freq. cum.
freq.		   score freq. cum.
freq.
0 0 0   23 2 11   46 3 112   69 0 215
1 0 0   24 0 11   47 5 117   70 0 215
2 1 1   25 6 17   48 6 123   71 3 218
3 0 1   26 1 18   49 4 127   72 1 219
4 0 1   27 3 21   50 9 136   73 4 223
5 0 1   28 2 23   51 7 143   74 5 228
6 0 1   29 5 28   52 7 150   75 1 229
7 0 1   30 2 30   53 5 155   76 0 229
8 0 1   31 1 31   54 1 156   77 3 232
9 0 1   32 4 35   55 2 158   78 1 233
10 2 3   33 1 36   56 6 164   79 0 233
11 0 3   34 9 45   57 7 171   80 0 233
12 0 3   35 4 49   58 6 177   81 1 234
13 0 3   36 4 53   59 3 180   82 2 236
14 0 3   37 7 60   60 8 188   83 1 237
15 0 3   38 8 68   61 2 190   84 1 238
16 0 3   39 11 79   62 1 191   85 1 239
17 0 3   40 8 87   63 6 197   86 1 240
18 2 5   41 4 91   64 1 198   87 1 241
19 3 8   42 5 96   65 6 204   88 1 242
20 0 8   43 4 100   66 3 207   89 0 242
21 0 8   44 4 104   67 6 213   90 2 244
22 1 9   45 5 109   68 2 215        
3p 3. Lees uit deze tabel af bij welke cesuur het percentage voldoendes het dichtst bij 25% ligt.

 
Men vraagt zich af of de verdeling uit de tabel redelijk benaderd kan worden door de normale verdeling. Het gemiddelde uit de tabel is 49,0 en de standaardafwijking 16,5.
6p 4. Onderzoek of de verdeling uit bovenstaande tabel voldoet aan de vuistregels van de normale verdeling.

Oppervlakte
Gegeven is de functie:  f(x) = √(x - 1)

De lijn k raakt de grafiek van f in het punt P(10,3). Zie de figuur hieronder.
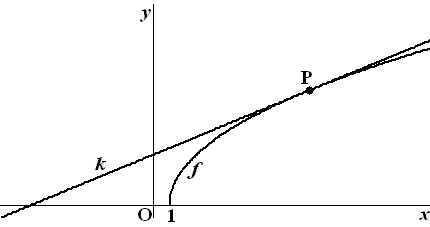5p 5. Stel met behulp van differentiëren een vergelijking op van k.
De grafiek van f  , de lijn k en de x-as sluiten een vlakdeel in.
7p 6. Bereken exact de oppervlakte van dit vlakdeel.
Kortste weg.
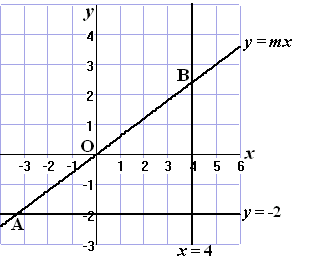
We bekijken de lijn l met vergelijking y = mx , met m > 0.
De lijn l snijdt de lijn y = -2 in A en de lijn x = 4 in B. Zie de figuur hierboven.
6p 7. Bewijs dat voor elke positieve waarde van m de lengte van lijnstuk AB gelijk is aan: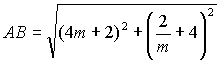

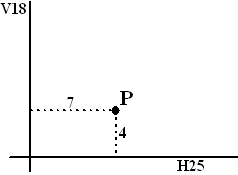
5p 8. Los nu het volgende probleem op:
Plaats P ligt dicht bij het kruispunt van twee wegen; de H25 en de V18. De wegen snijden elkaar loodrecht. Plaats P ligt 4 km van de H25 en 7 km van de V18 af.
Er wordt een nieuwe rechte weg aangelegd die de twee wegen met elkaar verbindt. De nieuwe weg moet door plaats P gaan.
Bereken in meters nauwkeurig de lengte van de kortste weg die aan deze eisen voldoet.

Schone-grond-verklaring
Om te mogen bouwen op een perceel grond is een zogeheten schone-grond-verklaring nodig.
Een onafhankelijke instantie neemt twee grondmonsters van zo'n perceel. Van elk perceel wordt in een laboratorium één monster getest op verontreiniging. Als er geen verontreiniging wordt aangetroffen wordt een schone-grond-verklaring afgegeven voor het betreffende perceel.

Ga in deze opgave uit van de volgende veronderstellingen:
Als de grond van een perceel verontreinigd is, wordt die verontreiniging in elk monster van dat perceel aangetroffen.
De kans dat een perceel verontreinigd is is 1%.
De kansen op verontreiniging voor verschillende percelen zijn onafhankelijk van elkaar.

Het testen van een monster is een kostbare zaak. In plaats van het afzonderlijk testen van de grond van elk perceel worden - om kosten te besparen - de grondmonsters van meerdere percelen bij elkaar gevoegd en als één geheel getest.

Veronderstel dat men grondmonsters van vijf percelen bij elkaar neemt en dit mengsel test. Als er geen verontreiniging in dit mengsel wordt aangetroffen, wordt voor elk van de betreffende percelen een schone-grond-verklaring afgegeven. Als er wel verontreiniging wordt aangetroffen test men van elk van de vijf percelen het tweede monster apart.
3p 9. Bewijs dat de kans dat men de tweede monsters zal moeten testen, afgerond op drie decimalen, gelijk is aan 0,049

Het nemen van twee grondmonsters van een perceel kost € 20,-. Een test in het laboratorium kost € 150,-.
6p 10. Toon aan dat de te verwachten kostenbesparing op het onderzoek van vijf percelen grond op deze manier € 563,25 is.

Uit de uitkomst van vraag 10 blijkt dat het inderdaad kostenbesparend is om een aantal monsters tegelijk te testen. Men vraagt zich af of een verdere kostenbesparing te realiseren is.
De grondmonsters van n percelen worden bij elkaar genomen.
5p 11. Bewijs dat de verwachtingswaarde van de kosten per perceel gelijk is aan :

170 + (150/n) - 150 • (0,99)n.

3p 12. Bereken bij welke waarde van n deze verwachtingswaarde minimaal is.

Een Lissajous-figuur
De bewegingsvergelijkingen: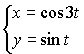



(met 0 ≤ t ≤ 2π) beschrijven de baan van een bewegend punt. Deze baan heeft precies vier punten met de y-as gemeen.
4p 13. Bereken de coördinaten van deze punten.
Tijdens de beweging verandert de snelheid van het punt voortdurend. De hoogste snelheid die het punt kan bereiken wordt enkele malen bereikt. Als je de beweging op de GR simuleert lijkt het alsof deze hoogste waarde bereikt wordt bij het passeren van de y-as.
8p 14. Toon aan dat dit niet het geval is.

Een verzameling toppen
Gegeven zijn de functies:
4p 15. Neem k = 1.
Bereken exact de coördinaten van de top van de grafiek van f1

Voor elke waarde van k ≠ 0 heeft de grafiek van fk één top.
De top van de grafiek van f1 ligt op een kromme met vergelijking  y = 1/x
6p 16. Bewijs dat voor elke waarde van k ≠ 0 de top van de grafiek van fk op de kromme y = 1/x ligt.

De waarde van k wordt zodanig gekozen dat de grafiek van fk de lijn y = 1 snijdt in de punten A en B. De lengte van AB hangt af van de keuze van k.
6p 17. Wat is de kleinste gehele waarde van k waarvoor de lengte van AB groter is dan 1? Licht je antwoord toe.

OPLOSSINGEN
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. NORMALCDF(0, 44.5 , 52.0 , 16.0) = 0,31904...en dat is ongeveer 32%.
2. Dan moet gelden  NORMALCDF(0 , X , 52.0 , 16.0) = 0,25
Voer in in de GR:  Y1 = NORMALCDF(0 , X , 52.0 , 16.0)
In de tabel zie je X = 41  geeft  Y1 = 0,24530...  en  X = 42 geeft  Y1 = 0,26540...
Dus de cesuur   41/42 geeft een percentage het dichtst bij 25%.
3. Het totaal aantal metingen is 244
25% daarvan is 61
Bij cesuur  37/38 is het aantal onvoldoendes 60, en dat ligt het dichtst bij 61.
4. De vuistregels zijn:

Tussen μ + σ en μ - σ ligt 68% van de metingen. In dit geval is dat tussen 49 + 16,5 = 65,5 en  49 - 16,5 = 32,5.
Bij 32 is de cumulatieve frequentie 35 en bij  65 is de cumulatieve frequentie  204.
Daartussen lagen dus 169 metingen, en dat is  (169/244) • 100% = 69,3%

Tussen μ + 2σ en μ - 2σ ligt 95% van de metingen.
In dit geval is dat tussen 49 + 2 • 16,5 = 82 en  49 - 2 • 16,5 = 16.
Bij 82 is de cumulatieve frequentie 236 en bij  16 is de cumulatieve frequentie  3.
Daartussen lagen dus 233 metingen, en dat is  (233/244)•100% = 95,5%

De vuistregels lijken redelijk goed te kloppen.
5. f ' (x) = 0,5 • (x - 1)-0,5  dus  f '(10) = 0,5 • (9)-0,5 =  1/6 en dat is het hellinggetal van de raaklijn.
De raaklijn heeft dus vergelijking y = (1/6) • x + b
b kun je vinden door het raakpunt (10,3) in te vullen:  3 = 10 • (1/6) + b dus  b = 4/3
Daarmee is de vergelijking geworden  y = 1/6 • x + 11/3
6. Bereken de oppervlakte onder de rechte lijn en trek er daarna de oppervlakte onder de wortel vanaf.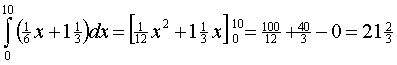


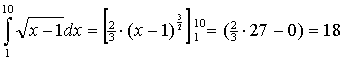
De gevraagde oppervlakte is dus  het verschil tussen deze twee en is  32/3
7. y = mx  snijden met  x = 4 geeft  y = 4m  en dus is  B = (4 , 4m)
y = mx  snijden met  y = -2 geeft  mx = -2 ofwel x = -2/m  en dus is  A = (-2/m , -2)
Pythagoras geeft dan :  AB2 =  (4 - - 2/m)2 + (4m - - 2)2 = (4 + 2/m)2 + (4m + 2)2
Door van beide kanten de wortel te nemen volgt de gevraagde vergelijking.
8. Leg een assenstelsel aan met de oorsprong in punt P.
Dan is de H25 de lijn met vergelijking y= -4 en de V18 de lijn met vergelijking x = -7 Noem AB = y = mx
Op dezelfde manier als in opgave 7 vinden we dan:

A = (-7 , -7m)  en  B = (-4/m , -4)
AB2 = (-4/m - - 7)2 + (-4 - -7m)2
AB2 = (7 - 4/m)2 + (7m - 4)2
AB = √{(7 - 4/m)2 + (7m - 4)2}

Plot Y1 = √{(7 - 4/X)2 + (7X - 4)2}
WINDOW bijv. Xmin = -5 , Xmax = 0 , Ymin = 0 , Ymax = 50
Bereken met CALC-minimum de minimumlengte.
Dat geeft  X = m = -0.829...  en  Y = AB = 15,363618.. km.
De kortste weg is  dus 15364 meter

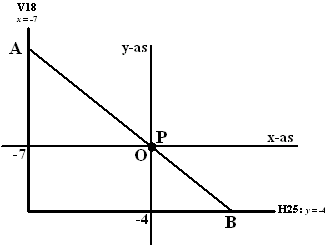9. P(tweede monsters moeten getest) = P(minstens één monster verontreinigd) = 1 - P(geen monster verontreinigd) =
= 1 - 0,995 = 1 - 0,95099.. = 0,0490099... - 0,049 (afgerond)
10. Bij apart meten kost het 5 • 150 = 750 euro.

In groepjes meten geeft kans 0,049 dat de tweede monsters getest moeten worden, en in dat geval zijn er 6 metingen gedaan dus zijn de totale kosten 6 • 150 = 900 euro.
De kans is 1 - 0,049 = 0,951 dat de tweede monsters niet getest hoeven te worden , in dat geval was er maar 1 meting nodig en zijn de koster 150 euro.
De gemiddelde kosten (verwachtingswaarde) zijn dus  900 • 0,049 + 150 • 0.951 = 186,75 euro.

Dat is een besparing van 750 - 186,75 = 563,25 euro.
11. Groepjes van n geeft kans  0,99n dat er maar één meting nodig is (alles schoon) en dus kans  1 - 0,99n dat alle tweede monsters gemeten moeten worden. In dat geval zijn er n + 1 metingen nodig.
Het gemiddelde aantal metingen voor n monsters is dus 
0,99n • 1 + (1 - 0,99n) • (n + 1) = 0.99n + n  + 1 - n • 0,99n - 0,99n = n + 1 - n • 0,99n
Per monster is dat (delen door n):  1 + (1/n) - 0,99n  metingen
De kosten zijn per meting 150 euro, dus totaal wordt dat  150 + 150/n - 150 • 0,99n  en daar komt nog 20 euro voor het nemen van de grondmonsters bij.
Samen in totaal 170 + 150/n - 150 • 0,99n
12. Voer in:  Y1 = 170 + 150/n - 150 • 0,99n  en kijk in de tabel.
Dat geeft een minimum bij n = 11 van 49,3356..... euro
13. y-as wil zeggen x = 0  dus  cos3t = 0
 ⇒ 3t = 0,5π (+ k • 2π)  of  3t = 1,5π (+ k • 2π)
 ⇒ t = 1/6π (+ k • 2/3π)  of  t = 0,5π (+ k • 2/3π)
Tussen 0 en 2π geeft dat de oplossingen t =  1/6π  ,  1/2π  ,  5/6π ,  7/6π  ,  3/2π  ,  11/6π
De bijbehorende y-waarden zijn respectievelijk:  1/2  ,  1  ,  1/2  ,  -1/2  ,  -1  ,  -1/2
De gevraagde punten zijn dus  (0 , 1/2) en (0, 1)  en  (0,-1/2)  en  (0, -1)
14. x' = -3•sin3t  en  y' = cost
snelheid = v = √(x'2 + y '2) = √(9sin23t + cos2t)
voer in Y1 = √(9sin23t + cos2t) en bereken met CALC-Maximum de maximale snelheid.
Tussen 0 en 2π geeft dat  X = 0,5182... en  1,5707.... en  2,6233... en  3,6598... en  4,7123... en  5,7649.....
Het passeren van de y-as was bij  t =  1/6π  ,  1/2π  ,  5/6π ,  7/6π   ,  3/2π  ,  11/6π (opgave 13)
Dat is resp. afgerond  0,5235... en  1,5707...  en  2,6179... en   3,66519... en  4,7123... en  5,7595...
Daaruit blijkt dat de hoogste snelheid niet altijd wordt bereikt bij het passeren van de y-as.
15.
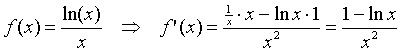
f'(x) = 0 geeft  1 - lnx = 0  ⇒ lnx = 1 ⇒ x = e
dat geeft  y = ln(e)/e = 1/e dus de top is het punt  (e , 1/e)
16.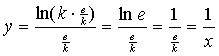
f'(x) = 0 geeft  1 - ln kx = 0  ⇒ ln kx = 1 ⇒ kx = e  ⇒ x = e/k
17. Hiernaast zie je een grafiekenbundel van  y = ln(kx)/x voor k = 1, 2, 3, 4, 5   en de lijn y = 1.
Makkelijk in te toetsen in de GR als  Y1 = ln({0,1,2,3,4,5}X)/X met gebruik van de "dikke komma" tussen de k-waarden
Het lijkt erop dat bij de rode grafiek de lengte van AB voor het eerst groter is dan 1.

Controle met  Y1 = ln(4x)/x en Y2 = 1 en INTERSECT geeft de punten (0.3574.. , 1)  en  (2.1532... , 1)  en de afstand daartussen is inderdaad meer dan 1.

Hetzelfde met Y1 = ln(3x)/x
geeft de punten (0.6190.. , 1) en  (1.5121... , 1) en de afstand daartussen is kleiner dan 1.

Dus voor k = 4 is de afstand AB voor het eerst groter dan 1.
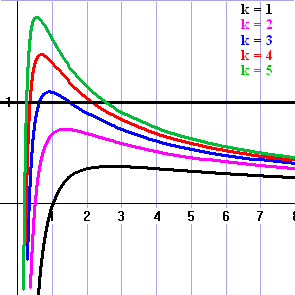