VWO WA, 2022 - III

 

Temperatuurschalen.
       
In Nederland drukken we temperaturen meestal uit in graden Celsius (°C), maar er bestaan veel meer temperatuurschalen. In deze opgave bekijken we een aantal van deze temperatuurschalen.

In de Verenigde Staten wordt de temperatuur uitgedrukt in graden Fahrenheit (°F). De Fahrenheitschaal is in 1724 ontwikkeld door de Duitser Gabriel Fahrenheit. Hij gebruikte bij het bedenken van deze schaal de volgende drie referentiepunten:
       
1. Hij maakte een mengsel van ijs, water en een bepaald soort zout. Dat was in die tijd de manier om een zo laag mogelijke temperatuur te verkrijgen.
Die temperatuur noemde hij 0 °F.
2. Het vriespunt van water. Dat noemde hij 32 °F.
3. De lichaamstemperatuur van een gezond mens. Die noemde hij 96 °F
       
In graden Celsius is de lichaamstemperatuur van een gezond mens gelijk aan 37 °C en is het vriespunt van water 0 °C. Zowel de Celsiusschaal als de Fahrenheitschaal is lineair. En ook het verband tussen de temperatuur in graden Celsius en die in graden Fahrenheit is lineair.
       
4p. 1. Bereken met behulp van de bovenstaande referentiepunten de temperatuur in °C van het ijsmengsel dat Fahrenheit gebruikte.
     

 
De metingen van Fahrenheit waren vrij onnauwkeurig en daarmee was zijn temperatuurschaal dat ook. Inmiddels is de Fahrenheitschaal nauwkeuriger vastgesteld en geldt tussen graden Celsius (C) en graden Fahrenheit (F) het volgende verband:   C = 5/9 • (F - 32).
       
3p. 2. Bereken bij welke temperatuur beide temperatuurschalen dezelfde temperatuur aangeven.
     

 
In de wetenschap werkt men meestal met de Kelvinschaal. Deze schaal is afgeleid van de Celsiusschaal, maar heeft een ander nulpunt, namelijk het zogenoemde absolute nulpunt. Dat is de laagst mogelijke temperatuur.
In graden Celsius is dat −273,15 °C.

Er geldt: K = C + 273,15 met K in Kelvin. Door de twee bovenstaande formules te gebruiken, kun je een formule opstellen die de temperatuur in Kelvin uitdrukt in graden Fahrenheit.
Deze formule heeft de vorm  K = aF + b
       
3p. 3. Bereken de waarden van a en b. Geef je antwoorden in twee decimalen.
     

 
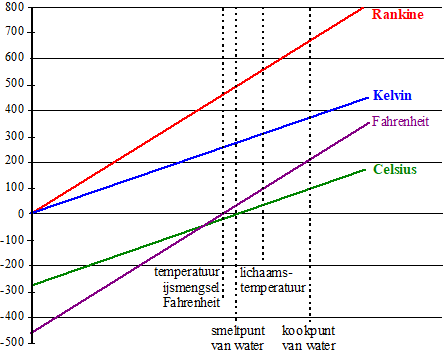
In de figuur zijn de grafieken getekend van verschillende temperatuurschalen: Celsius, Fahrenheit en Kelvin. Beide assen hebben een lineaire schaalverdeling. Op de horizontale as is echter geen schaalverdeling weergegeven: daar staan enkele natuurkundige verschijnselen die bij de betreffende temperaturen plaatsvinden. In de figuur is ook de grafiek getekend van de schaal van Rankine. Deze schaal is in de negentiende eeuw afgeleid van die van Fahrenheit, maar heeft, net als de Kelvinschaal, het absolute nulpunt als nulpunt. De grafieken die horen bij Fahrenheit en Rankine zijn evenwijdig.
       

       
Met behulp van deze grafieken en/of de voorgaande formules is het mogelijk om een verband op te stellen tussen de temperatuur in °C en die in graden Rankine (°Ra).

Dat verband heeft de vorm:   C = pR + q  met C de temperatuur in °C en R de temperatuur in °Ra.
       
4p. 4. Stel deze formule op. Licht je antwoord toe en geef de waarden van p en q in twee decimalen.
     

 
       
Zonkracht en beschermingsfactor.
       
Op de verpakking van een zonnebrandcrème staat de volgende tabel:
       
maximale tijd in de zon in uren en minuten  (bij zonkracht 8)
huidtype zonder crème met crème factor 20
1. zeer lichte huid 7,5 minuten 2 uur 30 minuten
2. lichte huid 12,5 minuten 4 uur 10 minuten
3. licht getinte huid 25 minuten 8 uur 20 minuten
4. getinte huid 37,5 minuten 12 uur 30 minuten
       
De beschermingsfactor van een zonnebrandcrème geeft aan met welke factor je de maximale tijd in de zon zonder crème moet vermenigvuldigen om de maximale tijd in de zon met crème te krijgen. Zo kun je in de tabel aflezen dat met huidtype 1 de maximale tijd in de zon zonder crème 7,5 minuten is. Met crème factor 20 is deze maximale tijd 20 maal zo lang.

Bovengenoemde tabel geldt voor zonkracht 8. De zonkracht is een maat voor de intensiteit van de zonnestraling. Zonkracht 8 is de maximale zonkracht die in Nederland voorkomt. Hoe lang iemand in de zon kan blijven, hangt niet alleen af van zijn huidtype en de zonnebrandcrème, maar ook van de zonkracht. Voor T, de maximale tijd in de zon zonder crème, wordt wel de volgende formule gebruikt:
       

       
Hierbij is T in minuten en heeft huidtype 1 huidwaarde 60, huidtype 2 huidwaarde 100, huidtype 3 huidwaarde 200 en huidtype 4 huidwaarde 300.

Er zijn zonnebrandcrèmes met beschermingsfactor 10, 15, 20, 30 en 50 beschikbaar.

Op een licht bewolkte dag in juni is de zonkracht 5. Iemand met huidtype 2 wil 4 uur in de zon kunnen blijven.
       
3p. 5. Bereken welke beschermingsfactor hij van bovenstaande beschikbare beschermingsfactoren minimaal nodig heeft in zijn zonnebrandcrème.
     

 
In werkelijkheid is de zonkracht gedurende een dag nooit constant, maar varieert afhankelijk van de bewolking en het moment van de dag. In de figuur zie je de gemeten zonkracht op 5 september 2015 in Bilthoven.
       

       
De met lijntjes verbonden punten geven de metingen aan. In de figuur is ook een grafiek getekend die de maximaal mogelijke zonkracht geeft, dat wil zeggen de zonkracht bij onbewolkte hemel. Onderzoekers benaderen deze grafiek met een formule van de vorm:   Z = a + bsin(c(t - d))
Hierin is Z de maximaal mogelijke zonkracht en t de tijd in uren.
       
4p. 6. Bepaal, met behulp van de figuur, de waarden van a, b, c en d in deze formule. Licht je antwoorden toe.
     

 
Op een bepaalde dag in augustus moet Marieke een lange tijd in de zon werken. Marieke heeft huidtype 1 en ze smeert zich altijd in met zonnebrandcrème factor 15. Je kunt nu berekenen dat Marieke maximaal 225 minuten in de zon kan blijven als de zonkracht constant 4 zou zijn.

Voor die dag in augustus is door een onderzoeker voor de maximaal mogelijke zonkracht Z de volgende formule opgesteld:

Z = 2,65 + 2,65sin(0,50(t - 10,7))
 
Hierin is t de tijd in uren met 7,6 ≤ t ≤ 20,1.
Neem aan dat de zon op deze dag de hele dag schijnt met de maximaal mogelijke kracht, dus volgens de formule.
       
4p. 7. Toon met behulp van deze formule aan dat Marieke met zonnebrandcrème factor 15 niet deze hele dag in de zon kan blijven.
     

 
       
       
Touwtjespringen.
       
Op veel schoolpleinen van basisscholen zie je groepen kinderen touwtjespringen. Twee kinderen draaien een lang touw rond, terwijl andere kinderen één voor één al springend het draaiende touw binnengaan en weer uitgaan.

In de figuur is een model van het springtouw in een assenstelsel getekend. De doorgetrokken lijn is het springtouw in de laagste stand en de stippellijn is het springtouw in de hoogste stand. Het springtouw wordt door de draaiers vastgehouden in de punten A en B. Het springtouw raakt de grond precies midden tussen de draaiers in. We gaan er in dit model van uit dat het springtouw symmetrisch om de as AB heen draait.
       

       
De formule die hoort bij de doorgetrokken lijn in de figuur is:
       

H(x) = e-0,31x + e0,31x + 2
       
Hierin is H(x) de hoogte (in meters) van het springtouw en x de ‘afstand’ (in meters) gemeten vanaf het punt waar het springtouw de grond raakt. In dit model verwaarlozen we de dikte van het springtouw. Het model is symmetrisch ten opzichte van de H-as en de maximale hoogte van de stippellijn in de figuur is 1,54 meter.

Uit de gegevens volgt dat de draaiers ongeveer 5,5 meter van elkaar staan.
       
4p. 8. Bereken de afstand tussen de punten A en B. Geef je antwoord in hele centimeters.
     

 
Bij een bepaald onderdeel van het spel moeten de kinderen rechtop onder het springtouw door rennen, zonder daarbij het touw te raken. Dat moeten ze zo dicht mogelijk bij een van de draaiers doen. Het is natuurlijk het handigst om het zo te doen dat je onder het touw door rent als het in de hoogste stand is.

Milan is 1,39 meter lang.
       
4p. 9. Onderzoek op welke afstand van de draaiers Milan minimaal moet rennen om het touw niet tegen zijn hoofd te krijgen. Geef je antwoord in hele centimeters.
     

 
Bij het touwtjespringen kunnen verschillende spelletjes gespeeld worden. Een groep van tien kinderen speelt zo’n spel. Bij dit spel wordt deze groep als volgt verdeeld:
- twee kinderen draaien met het touw, de zogenaamde draaiers;
- de overige acht kinderen worden in twee gelijke teams verdeeld.
       
4p. 10. Bereken hoeveel verschillende verdelingen er op deze manier mogelijk zijn.
     

 
Bij dit spel gaan de kinderen van een team één voor één het springtouw binnen. Het eerste kind maakt dan één sprong. Zodra het eerste kind één sprong gemaakt heeft, komt het tweede kind het springtouw binnen en samen maken ze twee sprongen. Na deze twee sprongen komt het derde kind het springtouw binnen en met z’n drieën maken ze vier sprongen. Tot slot komt het vierde kind binnen en met z’n vieren springen ze dan zes keer.
Direct na deze laatste sprongen verlaat het eerste kind het springtouw weer en kind 2, 3 en 4 volgen hem steeds met tussenpozen van drie sprongen. In totaal wordt er zo dus 22 keer gesprongen.

Hieronder zie je een gedeeltelijk ingevuld schema bij dit spel.
       
  aantal sprongen per kind totaal aantal
sprongen per kind
kind 1 1 2 4          
kind 2                
kind 3                
kind 4                
       
3p. 11. Vul het schema verder in en onderzoek hiermee welk kind de meeste sprongen maakt.
     

 
       
Hoe ver is de horizon?
       
Bij helder weer geldt: naarmate je hoger staat, kun je verder kijken. Maar is het ook zo dat je tweemaal zo ver kunt kijken als je tweemaal zo hoog staat? Dat onderzoeken we in deze opgave.

Daarvoor maken we een model: we beschouwen de aarde als een gladde bol. Zie de figuur.
       

       
De ogen van een waarnemer staan in punt A en de waarnemer kan tot punt H kijken: zó ver reikt zijn horizon. Punt M is het middelpunt van de aarde. Lijnstuk MH is een straal van de aarde; MH = 6371 km. De lengte van lijnstuk MA is 6371 km plus de hoogte van A boven de grond. De hoogte van A boven de grond noemen we x (in kilometers).
Driehoek AHM is rechthoekig. Met de stelling van Pythagoras AH 2 + HM 2 = AM 2  kunnen we nu de afstand AH (in kilometers) uitdrukken in x:

       
4p. 12. Toon aan dat de formule voor AH juist is.
     

 
Wie de Domtoren in Utrecht beklimt, kan op 75 meter ooghoogte en op 90 meter ooghoogte naar buiten kijken.
       
3p. 13. Bereken hoeveel je op 90 meter ooghoogte verder kunt kijken dan op 75 meter ooghoogte. Geef je antwoord in gehele km nauwkeurig.
     

 
Dat je verder kunt kijken als je hoger staat, betekent dat AH toeneemt als x toeneemt.
Uit de formule blijkt dat dit het geval is.
       
2p. 14. Beredeneer aan de hand van de formule van AH dat AH toeneemt als x toeneemt.
     

 
Ook door te differentiëren kun je aantonen dat AH toeneemt als x toeneemt.
       
5p. 15. Bepaal de afgeleide dAH/dx en beredeneer aan de hand van de formule van deze afgeleide, dus zonder een schets of tekening van de grafiek van de afgeleide te maken, dat AH toeneemt als x toeneemt.
     

 
Henk beweert dat, als je tweemaal zo hoog staat, je ook altijd tweemaal zo ver kunt kijken.
       
3p. 16. Onderzoek met behulp van de formule voor AH of Henk gelijk heeft.
     

 
       
Hypotheek.
       
In 2015 koopt Casper een nieuwe woning. Om die te kunnen betalen, sluit hij bij een bank een hypotheek af. Hij spreekt met de bank een periode af waarin hij de lening terugbetaalt, de looptijd van de hypotheek. Hierbij is het maandelijks te betalen bedrag gedurende de looptijd iedere maand hetzelfde. Dit bedrag bestaat voor een deel uit rente en voor een deel uit aflossing; deze aflossing is een terugbetaling van een gedeelte van het geleende bedrag.

De hoogte van de maandelijkse betaling wordt zó gekozen dat aan het eind van de looptijd de hypotheek precies is afgelost en alle rente is betaald.

De hypotheek van Casper is € 250000. Bij zijn hypotheek is de rente gedurende de gehele looptijd van 30 jaar hetzelfde, namelijk 4,3% rente per jaar over het nog terug te betalen deel van het geleende bedrag. Voor de restschuld van Casper kan de volgende recursieve formule worden opgesteld:

Rn = 1,0035 • Rn - 1  - B   met   R0 = 250000

In deze formule is Rn de restschuld (in euro’s) na n maanden en B het bedrag (in euro’s) dat hij per maand betaalt. De maandelijkse groeifactor is in deze formule afgerond op 4 decimalen tot 1,0035.
       
3p. 17. Bereken deze maandelijkse groeifactor in 5 decimalen nauwkeurig.
     

 
Voor de hypotheek van Casper geldt B = 1225,10 . Volgens zijn hypotheekadviseur is het zo dat hij na 10 jaar meer dan 20% van zijn hypotheek heeft afgelost.
       
4p. 18. Onderzoek of de hypotheekadviseur gelijk heeft.
     

 
Het bedrag dat Casper per maand betaalt, bestaat voor een deel uit rente (I) en voor een deel uit aflossing (F). Er geldt dus: B = I + F .

Aan het begin van de looptijd bestaat dit bedrag voor het grootste deel uit rente en slechts voor een klein deel uit aflossing, maar naarmate er meer afgelost wordt, neemt het rentedeel af en de aflossing toe.
Voor de hypotheek van Casper is met B =1225,10 het verloop van I en F weergegeven in de figuur.
       

       
Voor Casper kan de figuur aflossing van zijn hypotheek benaderd worden met de formule
F = 345,24 • e 0,0035n   met n in maanden.
       
4p. 19 Bereken na hoeveel maanden Casper voor het eerst meer aflossing dan rente betaalt.
     

 
In het algemeen geldt voor het berekenen van het maandelijks te betalen bedrag B de volgende formule:
       

       
In deze formule is L de hoogte van de lening, r het rentepercentage per maand en n de (resterende) looptijd van de lening in maanden.

Na 10 jaar bedraagt de restschuld van Casper nog € 198396.  Hij heeft op dat moment de mogelijkheid € 50000 van zijn hypotheek af te lossen. Het nadeel is wel dat hij dan voor de resterende looptijd van 20 jaar een nieuwe lening moet afsluiten met 0,375% rente per maand.
       
2p. 20. Toon aan dat het bedrag dat hij per maand moet betalen, gelijk wordt aan € 938,83 als hij € 50000 van zijn hypotheek aflost.
     

 
Casper heeft nu twee mogelijkheden: 
I Hij verandert niets aan zijn hypotheek en blijft € 1225,10 per maand betalen. De € 50000 zet hij op een lange-termijnspaarrekening waar hij 2,95% rente per jaar krijgt.
II Hij lost met de € 50 000 zijn hypotheek voor een deel af en betaalt nog maar € 938,83 per maand. Het geld dat hij per maand minder uitgeeft, zet hij op de bank maar hij ontvangt hier geen rente over.
       
5p. 21. Onderzoek welke mogelijkheid voor Casper het gunstigst is.
     

 
       
Wijkertunnel.
       
‘Banken verdienen fors aan Wijkertunnel’

In mei 2013 stond deze kop boven een artikel in het Financieel Dagblad over de Wijkertunnel. Deze tunnel, deel van de A9 tussen Velsen en Beverwijk, is gebouwd tussen 1993 en 1996 om de fileproblemen op de weg op te lossen.

Dit artikel is door vele kranten geciteerd.

Fragment uit het artikel
       
Wijkertunnel dubbel betaald
De staat verliest tot 2026 honderden miljoen euro’s op de Wijkertunnel bij Beverwijk. De tunnel is in de jaren negentig gebouwd met privaat geld. De afspraak was dat de overheid de investeerders ING en Commerzbank in 30 jaar zou terugbetalen afhankelijk van het gebruik van de tunnel. Doordat er veel meer auto’s doorheen gaan dan verwacht, betaalt de staat meer dan de bouw van de tunnel de investeerders heeft gekost.
       
Hieronder staan enkele infographics. Dat zijn figuren die de gemaakte berekeningen van het Financieel Dagblad toelichten. Met behulp van deze infographics kun je berekenen hoeveel meer de banken in de periode van 1996 tot 2026 betaald krijgen door de staat dan ze hebben uitgegeven aan de bouw van de tunnel.
       

       
Als de groei zoals die was in de periode 1997 tot en met 2010 zich zo voortzet tot en met 2025 dan gaan de banken inderdaad veel verdienen aan de tunnel.
       
7p. 22 Bereken met behulp van de infographics hoeveel de banken meer betaald krijgen dan ze uitgegeven hebben aan de bouw van de tunnel.
     

 
       

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. (C, F)  is  (0, 32) en  (37, 96)
rc is  (96 - 32)/(37 - 0) = 1,729...
F = 1,729C + 32
0 = 1,729C + 32
C = -18,5
   
2. C = F
C = 5/9 • (C - 32)
C = 5/9C - 17,77...
4/9C = -17,77...
C = -40 °C
   
3. K = C + 273,15
K = 5/9 • (F - 32) + 273,15
K = 5/9F - 5/9 • 32 + 273,15
K = 0,56F + 255,37
a = 0,56  en  b = 255,37
   
4. De lijnen van Fahrenheit en Rankine zijn evenwijdig dus hebben ze dezelfde richtingscoëfficiënt.
Dat betekent dat p = 5/9 = 0,56
0 °RA = 0 °K = -273,15 °C
Dus q = -273,15
   
5. huidwaarde  = 100
zonkracht = 5
T = 100/5 = 20 minuten zonder crème
4 uur  = 240 minuten
240/20 = 12  dus factor 12 is nodig
De minimale beschikbare factor is factor 15.
   
6. top Z = 4, minimum Z = 0
Dus de evenwichtslijn is a = 2  en de amplitude is  b = 4 - 2 = 2
periode is 12 uur, dus  c = 2π/12 = π/6
Top bij t = 13,7  dus het beginpunt een kwarperiode daarvoor, dus bij  13,7 - 3 = 10,7
Dus d = 10,7
   
7. Hoe lang is de zonkracht 4 of hoger?

Y1 =  2,65 + 2,65sin(0,50(t - 10,7))
Y2 = 4
intersect geeft  t = 11,7... en t = 15,9...
Daartussen ligt  15,9 - 11,7 = 4,2 uur
Dat is meer dan 4 uur
Zelfs bij zonkracht precies 4 mag ze maar 225 minuten in de zon blijven en dat is al korter dan 4 uur.
   
8. Het hoogste punt is 1,54 m en omdat de figuur symmetrisch is zitten A en B dus op een hoogte 0,77 m
Y1 = e-0,31x + e0,31x + 2
Y2 = 0,77
intersect geeft  x = 2,746....
De afstand AB is het dubbele daarvan:   5,49 m
   
9. 1,54 - 1,39 = 0,15
De stippellijn heeft bij het grensgeval afstand 0,15 tot het hoogste punt
Dan heeft de doorgetrokken lij n afstand 0,15 tot de boden.
Y1 = e-0,31x + e0,31x + 2
Y2 = 0,15
intersect geeft   x = 1,24...
De afstand tot de draaier is dan  2,75 - 1,24 = 1,51 m
   
10. Kies er twee uit de 10 voor de draaiers:  10 nCr 2 = 45 mogelijkheden
Kies er daarna 4 uit de acht voor team 1:  8 nCr 4 = 70 manieren
in totaal dus 45 • 70 = 3150 manieren.
maar elke is nu dubbel geteld, want team 1 en team 2 verwisselen geeft dezelfde onderverdeling.
dus blijven over 3150/2 = 1575  manieren.
   
11.
  aantal sprongen per kind totaal aantal
sprongen per kind
kind 1 1 2 4 6 - - - 13
kind 2 - 2 4 6 3 - - 15
kind 3 - - 4 6 3 3 - 16
kind 4 - - - 6 3 3 3 15

Het derde kind maakt de meeste sprongen.
   
12. AH 2 + HM 2 = AM 2
AH 2 = AM 2  - HM 2 
AM  = x + 6371
HM = 6371
AH2 = (x + 6371)2 - 63712
AH 2 = x2 + 12742x + 63712 - 63712
AH 2 = x2 + 12742x
AH = √(x2 + 12742x)
   
13. x = 90  geeft  AH = √(12742 • 0,09 + 0,092 ) = 33.8... km
x = 75  geeft  AH = √(12742 • 0,075 + 0,0752 ) = 30,9... km
Het verschil is ongeveer 3 km.
   
14. Als x toeneemt dan nemen 12742x en x2 beiden ook toe
Dan neemt het deel onder de wortel dus ook toe
Dan neemt de wortel zelf ook toe.
   
15. AH = (12742x + x2)0,5
AH ' =  0,5(12742x + x2)-0,5 • (12742 + 2x)
omdat x > 0 is  alles positief, dus  AH ' is altijd positief, dus AH neemt toe.
   
16. x = 10 geeft  AH = √(12742 • 10 + 102) = 357,09...
x = 20 geeft  AH = √(12742 • 20 + 202) = 505,21.....
Dat is niet het dubbele, dus het is NIET WAAR.
   
17. bij 4,3% hoort een groeifactor 1,043
Voor de g per maand geldt dan  g12 = 1,043
g = 1,04431/12 = 1,00351
   
18. Invoeren in de GR
Mode seq
nmin = 1
u(n) = 1,0035*u(n - 1) - 1225,10
TABLE geeft dan bij n = 120  dat  R = 197901
80% van 250000 is 200000
De hypotheekadviseur heeft gelijk.
   
19. 1225,10 = I + F
Als I en F gelijk zijn dan is dus F = 612,55
612,55 = 345,24 • e 0,0035n 
1,77... = e 0,0035n 
ln(1,77...) = 0,0035n
0,5733.. = 0,0035n
n = 163,82...
Dus F is voor het eerst groter dan I  na 164 maanden
   
20. De restschuld is nu € 198396
Als hij 50000 aflost is de restschuld nog € 148396
20 jaar betekent dat n = 240
Dat geeft  B = 148396 • (0,01 • 0,375)/(1- (1 + 0,01 • 0,375)-240) = 938,83
   
21. I:
240 • 1225,10 = 294024
50000 • 1,029520 = 89432,84
Dat kost uiteindelijk  294024 - 89432,84 = 204591,16

II:
240 • 938,83 = 225319,20

Methode I is voordeliger.
   
22. Het aantal auto's neemt vanaf 1997 ongeveer lineair toe.
Het gemiddelde jaar in de periode 1997-2025 is het jaar 2011
In dat jaar reden er ongeveer 43 mln auto's door de tunnel.
Dat leverde de banken  dat jaar  43 mln • 0,53 = 22,79 mln.
De hele periode is 29 jaar, dus dat geeft  29 • 22,79 =660,91 mln euro.
In 1996 was de opbrengst   15 mln • 0,53 = 7,95 mln.
Samen is dat 660,91 + 7,95 = 669 mln euro voor de banken.

De investering was 185 mln.
De winst voor de banken is dus 669 - 185 = 484 mln euro.