Nieuwe pagina 1

Asperges.

Vooral in Zuid-Nederland worden asperges als groente geteeld. Uit aspergezaad groeien aspergeplanten en als deze voldoende gegroeid zijn, worden de asperges geoogst.

De prijs van het zaad is € 4500 per kg. Per hectare groeien ongeveer 20000 aspergeplanten. Hiervoor is ongeveer 750 gram zaad nodig. Een aspergeplant levert in een oogstseizoen gemiddeld twintig asperges. In één kilo gaan gemiddeld tien asperges.
De gemiddelde opbrengst van één kilo asperges is € 4.

4p.

Bereken het verschil van de gemiddelde opbrengst per hectare en de kosten voor het benodigde zaad.

De geoogste asperges worden op basis van kleur en dwarsdoorsnede gesorteerd. In deze opgave bekijken we witte asperges met een dwarsdoorsnede van 10 tot 38 mm. Een aspergeteler heeft in een week in mei 20 000 asperges geoogst en daarna gesorteerd. In de volgende tabel staan de aantallen per klasse weergegeven.

klasse	dwarsdoorsnede (in mm)	frequentie
C1	10 - < 12	1600
B1	12 - < 16	4000
A1	16 - < 20	4500
AA1	20 - < 28	8800
AAA1	28 - < 38	1100

5p.

Zet de gegevens uit deze tabel uit op normaal waarschijnlijkheidspapier en toon daarmee aan dat de dwarsdoorsneden van de geoogste asperges van deze aspergeteler bij benadering normaal verdeeld zijn.

We nemen vanaf nu aan dat we de dwarsdoorsneden van asperges mogen benaderen met de normale verdeling met μ = 20,1 mm en σ = 5,6 mm. Zoals in de tabel te zien is, verdelen we de asperges in vijf klassen.
We kunnen nu het percentage asperges in klasse AA1 berekenen met behulp van de normale benadering, maar ook met behulp van de gegevens uit de tabel.

4p.

Bereken deze beide percentages. Rond je antwoord af op hele percentages.

Op een ochtend oogst een andere aspergeteler 200 asperges. Neem weer aan dat de dwarsdoorsneden van asperges benaderd mogen worden met de normale verdeling met μ = 20,1 mm en σ = 5,6 mm.

5p.

Bereken hoe groot de kans is dat er van de 200 geoogste asperges minstens 50 in klasse A1 zitten.

Topinkomens.

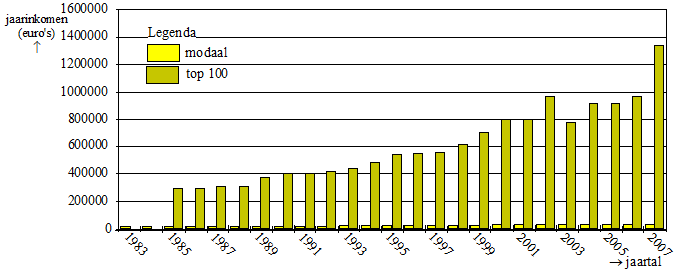
Op 17 mei 2008 stond in de Volkskrant een artikel waarin gesteld werd dat de salariskloof tussen topbestuurders en gewone werknemers in Nederland steeds groter wordt. Bij het artikel was een figuur afgedrukt waarin het gemiddelde van de 100 topinkomens en het modale inkomen in de periode 1983-2007 te zien waren. Zie onderstaande figuur. Alle bedragen in deze figuur zijn jaarinkomens in euro’s.

De Volkskrant stelt dat in de periode 1983-2007 de inkomens van topbestuurders elk jaar met gemiddeld 7,2% zijn gestegen. In de figuur staan geen gegevens over topinkomens in 1983 en 1984 omdat die toen nog niet openbaar waren.
In 1985 was het gemiddelde van de 100 topinkomens € 295000.

Uitgaande van het bedrag voor 1985 levert een gemiddelde groei van 7,2% per jaar inderdaad ongeveer het gemiddelde jaarsalaris van de 100 topinkomens op zoals dit in de figuur bij 2007 af te lezen is.

4p.

Bereken dit gemiddelde jaarsalaris en vergelijk je antwoord met het gemiddelde jaarsalaris dat in de figuur af te lezen is.

In de figuur is ook te zien dat het gemiddelde topinkomen in 2007 aanzienlijk hoger was dan in 2006. In 2006 was het gemiddelde jaarsalaris van de 100 topinkomens € 980000. Als men met de gegevens van 1985 en 2006 berekent met hoeveel procent het gemiddelde jaarsalaris van de 100 topinkomens gestegen is, komt men niet uit op 7,2% per jaar maar op een lager percentage.

4p.

Bereken dit percentage in één decimaal nauwkeurig.

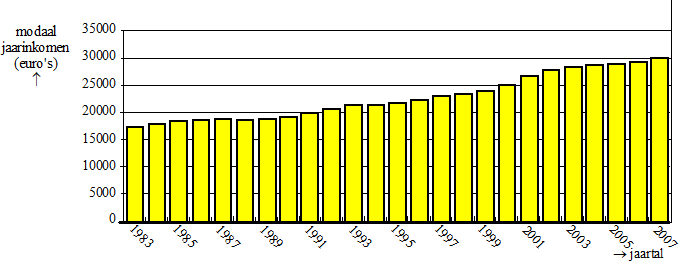
De kleine staafjes van het modale jaarinkomen uit de eerste figuur zijn in bovenstaande figuur nogmaals weergegeven. Het modale jaarinkomen is een maat voor het salaris van de “gewone werknemer”: veel mensen verdienen een salaris dat rond dit bedrag ligt. In 1983 verdiende een topbestuurder uit de top-100 gemiddeld 16 keer zoveel als het modale inkomen en in 2007 gemiddeld 44 keer zoveel.

4p.

Toon aan dat het gemiddelde jaarsalaris van de 100 topinkomens in 2007 ongeveer 5 keer zo hoog was als in 1983.

Ook binnen de 100 topinkomens zijn nog grote verschillen. In 2004 was het gemiddelde jaarsalaris van de 100 topinkomens € 910000. Het gemiddelde jaarsalaris van de 25 hoogste inkomens uit deze groep was € 1720000.

4p.

Onderzoek of de 25 topbestuurders met de hoogste inkomens gemiddeld meer dan drie keer zoveel verdienen als het gemiddelde van de rest van de bestuurders uit deze top-100.

Op de website van de Volkskrant kan iemand laten berekenen hoeveel hij zou verdienen als zijn salaris de afgelopen 25 jaar evenveel gestegen was als dat van topbestuurders. Op de website staat de onderstaande tekst:

Hoe hoog zou jouw topsalaris moeten zijn? Kruip in de huid van een topbestuurder en doe net alsof je salaris in de afgelopen 25 jaar even hard opliep als het inkomen van de hoogste baas. Vul je huidige salaris in en zie wat je eigenlijk had moeten verdienen. Voor het gemak is ervan uitgegaan dat je er de afgelopen 25 jaar net als Jan Modaal maar 2,3 procent per jaar aan salarisverhoging bij hebt gekregen, terwijl Jan Top er jaarlijks 7 procent op vooruitging.

Bij ieder salaris dat je invult als huidig salaris geeft de website een salaris als antwoord. Dit antwoord is het salaris dat je zou verdienen als je salaris even snel gestegen zou zijn als dat van topbestuurders. Het blijkt dat de website dan als antwoord een salaris geeft dat ongeveer 3 maal zo hoog is als je huidige salaris.

4p.

Bereken in twee decimalen nauwkeurig hoeveel maal zo hoog het antwoord van de website is.

Zuivere dobbelsteen ?

Op de foto zie je twee ronde dobbelstenen. Op deze dobbelstenen staan aantallen ogen van 1 tot en met 6, net als op gewone dobbelstenen. Een ronde dobbelsteen is hol met binnenin een stalen kogeltje. Bij elk getal zit in de holle binnenkant een soort kuiltje waar het kogeltje in past. Aan het einde van een worp komt het kogeltje in zo’n kuiltje terecht. Hierdoor blijft de dobbelsteen liggen, bijvoorbeeld met de vier onder en de drie boven: er is dan drie gegooid.

Of een dobbelsteen zuiver is of niet, kun je onderzoeken door er een groot aantal keer mee te gooien. Dit wordt geïllustreerd door de volgende figuur. In deze figuur is het resultaat te zien van een aantal simulaties van het gooien met een zuivere dobbelsteen. Er werd hierbij alleen gekeken naar het aantal drieën.



Elk cirkeltje stelt het resultaat van een simulatie voor. Langs de horizontale as is het aantal worpen bij een simulatie uitgezet op een logaritmische schaalverdeling. Langs de verticale as staat de relatieve frequentie van het aantal drieën dat hierbij gegooid is. In de figuur is bijvoorbeeld te zien dat bij de simulatie van 10 worpen de relatieve frequentie 0,1 is: er is precies één keer een drie gegooid. Bij een simulatie van 60 worpen is 4 keer een drie gegooid.

3p.	10.	Teken het punt dat bij deze simulatie hoort in de figuur. Licht je werkwijze toe.

In de figuur is de verwachte relatieve frequentie aangegeven met een horizontale lijn op een hoogte van ongeveer 0,167. Dit komt overeen met kans ¹/₆. Het punt dat hoort bij de simulatie van 200 worpen ligt dichter bij deze horizontale lijn dan het punt dat hoort bij de simulatie van 30 worpen. Bij de simulatie van 200 worpen is het verschil tussen de verwachte en de werkelijke relatieve frequentie dus kleiner. We kunnen ook kijken naar de verschillen bij het aantal geworpen drieën. Rik beweert dat het verschil tussen het werkelijke en het verwachte aantal geworpen drieën bij de simulatie van 200 worpen kleiner is dan bij de simulatie van 30 worpen.

5p.	11.	Onderzoek of Rik gelijk heeft.

Als het aantal gesimuleerde worpen groter wordt, komen de punten van de simulaties steeds dichter bij de horizontale lijn te liggen. De resultaten van de simulaties benaderen de werkelijke kans van ¹/₆ dan steeds beter. Dit is ook theoretisch te berekenen. Het aantal geworpen drieën bij een simulatie van n keer gooien is voor grote waarden van n te benaderen met een normale verdeling. Hiermee kan men berekenen dat voor een simulatie van 10000 worpen geldt: de kans dat de relatieve frequentie van het aantal geworpen drieën minder dan 1% van ¹/₆ verschilt, is ongeveer 0,35. Voor een simulatie van 100000 worpen is deze kans veel groter.

6p.	12.	Laat dit met een berekening zien.

Jesse vermoedt dat de kans om met zijn ronde dobbelsteen drie te gooien kleiner is dan ¹/₆. Na het zien van de figuur besluit hij om 600 keer met zijn ronde dobbelsteen te gooien om dit te onderzoeken. Na 600 keer gooien heeft hij 87 keer drie gegooid.

6p.	13.	Onderzoek of Jesse op grond van dit steekproefresultaat mag concluderen dat de kans om met deze dobbelsteen drie te gooien kleiner is dan ¹/₆. Neem een significantieniveau van 5%.

Bouwgrafiek.

Bij nieuwbouw stellen gemeentes bestemmingsplannen op om onder meer te voorkomen dat een nieuwe wijk een rommelig aanzicht krijgt. In het bestemmingsplan voor de wijk “Den Brabander fase 2” van de gemeente Alphen-Chaam is de volgende grafiek opgenomen.



In de nieuwe wijk wordt een aantal bouwpercelen verkocht. Een bouwperceel is een stuk grond waarvan een gedeelte bebouwd mag worden. In de grafiek kun je aflezen hoeveel vierkante meter bij een bepaalde oppervlakte van een bouwperceel maximaal bebouwd mag worden. Voorbeeld: van een bouwperceel met een oppervlakte van 300 m² mag maximaal 175 m² bebouwd worden. Mevrouw Groen koopt een bouwperceel van 20 bij 20 meter. Zij wil precies de maximaal toegestane oppervlakte aan bebouwing gebruiken voor een vierkant huis. Op de overige grond wil zij rondom het huis grindpaden van 3 meter breed aanleggen.

4p.	14.	Onderzoek of dit te realiseren is.

Een architectenbureau hanteert als vuistregel dat van een bouwperceel maximaal 20 m² meer dan de helft van de oppervlakte bebouwd zou mogen worden. In formulevorm: B = 0,5p + 20 Hierin is B de maximale oppervlakte aan bebouwing in m² en p de oppervlakte van een bouwperceel in m².

3p.	15.	Gebruik de grafiek om te bepalen vanaf welke perceelgrootte de regeling die is weergegeven in de grafiek strenger is dan deze vuistregel.

De bouwpercelen zijn minstens 100 m² groot. Voor bouwpercelen van 500 m² tot 800 m² neemt de maximale bebouwing lineair toe. Van geen enkel bouwperceel mag meer dan 240 m² bebouwd worden. De grafiek bestaat dus uit drie delen: van 100 tot 500, van 500 tot 800 en vanaf 800. De drie delen van de grafiek kunnen we elk karakteriseren met een beschrijving uit de volgende lijst: - toenemend stijgend - constant stijgend - afnemend stijgend - constant - afnemend dalend - constant dalend - toenemend dalend. Tussen 100 en 500 is de grafiek afnemend stijgend, van 500 tot 800 constant stijgend en vanaf 800 constant. Met behulp van de grafiek kunnen we ook een grafiek tekenen van de oppervlakte die minimaal onbebouwd moet blijven. Ook de drie delen van deze nieuwe grafiek kunnen we karakteriseren met behulp van bovenstaande lijst.

4p.	16.	Geef voor elk van de drie delen van de nieuwe grafiek een karakterisering. Geef een toelichting.

Energie.

Een machine, zoals een automotor, gebruikt energie in de vorm van brandstof. Een machine levert ook energie, maar de hoeveelheid geleverde energie is altijd kleiner dan de hoeveelheid energie die erin wordt gestopt. Wanneer de hoeveelheid energie die een machine levert 30% is van de hoeveelheid energie die erin wordt gestopt, spreken we van een machine met een rendement R = 0,3. De resterende 70% energie gaat verloren, bijvoorbeeld in de vorm van warmte. Het rendement is daarom altijd kleiner dan 1. Aan het einde van de vorige eeuw schreef de Amerikaanse onderzoeker J. Ausubel een artikel met de titel ‘Can technology spare the earth?’. Daarin beschrijft hij de ontwikkeling van nieuwe machines die een hoger rendement hebben en waarmee dus veel brandstof bespaard kan worden. In het artikel van Ausubel komt een grafiek voor die de ontwikkeling van het rendement van een aantal machines weergeeft. Zie de figuur.



Op de verticale as zie je een logaritmische schaalverdeling.

In deze formule is R het rendement van de machine. Een van de machines uit deze figuur heeft een rendement van 0,43.

3p.	17.	Ga met behulp van een berekening na welke machine in de figuur hier bedoeld wordt.

De punten in de figuur geven een trend aan die met de rechte lijn aangegeven wordt. Het laatste stuk van deze rechte lijn is een voorspelling voor de komende jaren. Zo voorspelt Ausubel een brandstofcel (Fuel Cell) met een hoog rendement. Uit de figuur volgt dat hiervoor geldt dat R* = 2 .

3p.	18.	Bereken hoe groot het rendement van deze brandstofcel volgens Ausubel is.

In de figuur is niet R, maar R* weergegeven ten opzichte van de tijd. Dit is gedaan omdat de grafiek dan een rechte lijn wordt als op de verticale as een logaritmische schaalverdeling wordt gebruikt. Het gebruik van R* levert geen problemen op omdat bij elke waarde van R* precies een waarde van R hoort. Op grond van de formule R^* = ^R/_{(1 - R)}kunnen we beredeneren dat als R toeneemt van 0 tot 1, dat R* dan ook steeds toeneemt.

4p.	19.	Geef deze redenering.

In de figuur is de grafiek van R* een rechte lijn. Dat betekent dat de formule voor R* van de vorm R* = b • g^t is, met t de tijd in jaren en t = 0 voor het jaar 1700. Uit de figuur lezen we af dat bij 1700 de waarde R* = 0,01 hoort en bij 2050 de waarde R* = 2 .

3p.	20.	Bereken de waarden van b en g.

UITWERKING

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

opbrengst.
20000 planten met 20 asperges per plant betekent 20000 • 20 = 400000 asperges per ha.
dat is 400000/10 = 40000 kilo asperges.
dat levert 40000 • 4 = 160000 euro op.

kosten.
voor 1 ha is 750 gram zaad nodig, en dat is 0,75 kg.
Dat kost 0,75 • 4500 = 3375 euro

Het verschil tussen opbrengst en kosten is 160000 - 3375 = 156625 euro.

klasse	dwarsdoorsnede (in mm)	rechter- klassengrens	frequentie	cumulatieve frequentie	relatieve cumulatieve frequentie
C1	10 - < 12	12	1600	1600	8%
B1	12 - < 16	16	4000	5600	28%
A1	16 - < 20	20	4500	10100	50,5%
AA1	20 - < 28	28	8800	18900	94,5%
AAA1	28 - < 38	38	1100	20000	100%

De derde kolom op de x-as en de laatste op de y-as geeft een rechte lijn op normaal-waarschijnlijkheidspapier.
Dus de dwarsdoorsneden zijn bij benadering normaal verdeeld.

P(20 ≤ X < 28) = normalcdf(20, 28, 20.1, 5.6) = 0,4279... = 43%

tabel: 8800 van de 20000 is 44%

de kans dat een asperge in klasse A1 zit is normalcdf(16, 20, 20.1, 5.6) = 0,2608...

binomiale verdeling: n = 200 en p = 0,2608...
P(X ≥ 50) = 1 - P(X ≤ 49) = 1 - binomcdf(200, 0.2608, 49) = 0,6623...

een groei van 7,2% betekent een groeifactor g = 1,072
de beginwaarde is 295000 en het gaat om een periode van 22 jaar.
Dan geldt y = 295000 • 1,072²² = 1361781 dus ongeveer 1 360 000
Dat klopt redelijk met het salaris uit de figuur.

de groei is van 295000 naar 980000 en dat is een groeifactor ⁹⁸⁰⁰⁰⁰/₂₉₅₀₀₀ = 3,322...
Maar dat is in een periode van 21 jaar, dus per jaar is dat een factor 3,322..^1/21 = 1,0588...
Dat betekent een jaarlijks percentage van 5,9%

in 1983 was het modale salaris ongeveer 17000 dus het gemiddelde top-100 salaris 16 • 17000 = 272000
in 2007 was het modale slaris ongeveer 30000 dus het gemiddelde top-100 salaris 44 • 30000 = 1320000
Dat scheelt een factor ^1320000/₂₇₂₀₀₀ = 4,8....
Dat is ongeveer 5 keer zo hoog.

(het kan natuurlijk ook met de groeifactor 1,072: 1,072²⁴ = 5,3 dus ongeveer 5. (Maar ja, waarom zouden dan al die gegevens over het modale inkomen in de opgave staan?)

100 inkomens die gemiddeld 910000 zijn, betekent een totaal inkomen van 100 • 910000 = 91000000
de 25 hoogstens hebben gemiddeld 1720000 dus een gezamenlijk inkomen van 25 • 1720000 = 43000000
dan blijft er voor de andere 75 nog 91000000 - 43000000 = 48000000 over.
Gemiddeld is dat ^48000000/₇₅ = 640000
3 • 640000 = 1920000 en dat is meer dan 1720000 dus de hoogste 25 verdienden niet meer dan drie keer zoveel.

het salaris van Jan Modaal wordt per jaar vermenigvuldigd met 1,023. Dat geeft in 25 jaar een vermenigvuldiogiong met 1,023²⁵= 1,766Een topsalaris wordt elk jaar met 1,07 vermenigvuldigd. Dat egeft e=uin 25 jaar een vermenigvuldiging met 1,07²⁵ = 5,427
Dat is dus ^5,427/_1,766 = 3,07 keer zo hoog.

10.

4 van de 60 is kans ⁴/₆₀ = 0,067
zie de figuur.

11.

Bij 30 worpen is de relatieve frequentie ongeveer 0,10. Dat betekent dat er 0,1 • 30 = 3 keer een 3 is gegooid.
Het verwachte aantal was ¹/₆ • 30 = 5 dus dat scheelt 5 - 3 = 2

Bij 200 worpen was de relatieve frequentie ongeveer 0,13. Dat betekent dat er 0,13 • 200 = 26 keer een drie is gegooid.
Het verwachte aantal was ¹/₆ • 200 = 33¹/₃ dus dat scheelt 33¹/₃ - 26 = 7¹/₃

7¹/₃ is meer dan 2 dus Rik heeft geen gelijk.

12.

Voor 100000 worpen geldt μ = ¹⁰⁰⁰⁰⁰/₆ = 16666²/₃ en σ = √(100000 • ¹/₆ • (1 - ¹/₆)) = 117,85...
1% afwijking van 16666²/₃ is een afwijking van 166²/₃ worpen.
Het aantal zal dus tussen 16666²/₃ - 166²/₃ = 16500 en 16666²/₃ + 166²/₃ = 16833¹/₃ moeten liggen
P(16500 < X < 16833¹/₃) = normalcdf(16500, 16833¹/₃, 16666²/₃, 117,85...) = 0,84..
Dus de kans is veel groter.

13.

H₀: p = ¹/₆
H₁: p < ¹/₆
de meting is 87 van de 600 keer.
overschrijdingskans: P(X ≤ 87) = binomcdf(600, ¹/₆, 87) = 0,0836....
Dat is groter dan 0,05 dus H₀ aannemen: Jesse mag NIET concluderen dat de kans om 3 te gooien kleiner is dan ¹/₆.

14.

aflezen uit de figuur: de oppervlakte van het huis wordt 200 m²
de zijden van het huis zijn dan √200 = 14,1421... meter.
voor het hele perceel komt daar tweemaal een breedte van 3 meter bij,
dus dat krijgt zijden van 14,1421 + 6 = 20,1421....
Maar dan zou de oppervlakte meer dan 400 m² worden, want 20,1421² = 405,7..., dus dit is niet te realiseren.

15.

teken de lijn B = 0,5p + 20 (door bijv (0, 20) en (100, 70)
snijpunt aflezen: p = 323
vanaf p = 323 is de regeling strenger want daar ligt de grafiek van de regeling onder de lijn B = 0,5p + 20.

16.

p	100	200	300	400	500	600	700	800
bebouwd	70	137,5	175	200	217,50	225	232,50	240
onbebouwd	30	62,5	125	200	282,5	375	467,5	560

tussen 100 en 500 (blauwe deel) is er toenemende stijging (de toenames zijn 32,5 - 62,5 - 75 - 82,5)
tussen 500 en 800 (paarse deel) is er constante stijging (de toenames zijn steeds 92,5)
vanaf 800 is er constante stijging immers als p toeneemt en het bebouwde deel blijft gelijk, dan moet het onbebouwde deel even hard als p toenemen.

17.

R^* = ^0,43/_{(1 - 0,43)} = ^0,43/_0,57 = 0,754....
in de figuur zie je dat dat hoort bij Gas Turbine.

18.

R^* = 2 geeft ^R/_{(1 - R)} = 2
R = 2(1 - R)
R = 2 - 2R
3R = 2
R = ²/₃

19.

Als R groter wordt, dan wordt 1 - R kleiner.
Dus van R^* wordt de teller groter en de noemer kleiner.
Dus R^* neemt toe.

20.

b = 0,01 want dat is de beginwaarde.
2050 hoort bij t = 350
(350, 2) invullen: 2 = 0,01 • g³⁵⁰
g³⁵⁰ = ²/_0,01 = 200
g = 200^1/350 = 1,01525...

VWO WA, 2018 - II Bezem.