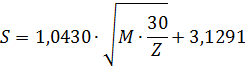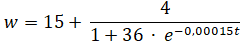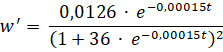VWO WA, 2016 - II  PILOT
SMOG - index
       

Er is veel onderzoek gedaan naar de moeilijkheidsgraad van teksten. Er zijn dan ook verschillende manieren om die in een getal uit te drukken. Deze opgave gaat over één van die manieren.

Begin 2014 publiceerde NRC Handelsblad het volgende fragment uit een artikel over de gebruiksvoorwaarden van Googlesoftware.
       
Fragment.

Google’s gebruiksvoorwaarden worden met argusogen gevolgd door privacywaakhonden als Bits of Freedom en het College Bescherming Persoonsgegevens. Ze hebben het vaak over de inhoud van zulke teksten, maar hoe zit het met de moeilijkheidsgraad van de teksten? Die is hoog bij Google’s privacyvoorwaarden, volgens SMOG, de methode waarmee de moeilijkheidsgraad van een tekst berekend wordt aan de hand van woordlengte en zinlengte (hoe langer, hoe moeilijker).
       

De SMOG-index van een tekst geeft het aantal jaar opleiding aan dat nodig is om de tekst te kunnen begrijpen. Je berekent de SMOG-index (S) met de formule:
       

       

Hierin is M het aantal woorden van drie of meer lettergrepen en Z het aantal zinnen.
Voor bovenstaand fragment geldt dat M = 14.
       

3p.

1.

Bereken de SMOG-index van de tekst in het fragment. Rond je antwoord af op een geheel getal.
   

 

Als de SMOG-index van een tekst te hoog is, kun je de tekst herschrijven. Als je bij het herschrijven van een tekst 15% minder woorden met drie of meer lettergrepen gebruikt, wordt S kleiner. Maar die verkleining van S had je ook kunnen bereiken door de tekst alleen te herschrijven in meer zinnen.
       

4p.

2.

Bereken hoeveel procent meer zinnen die nieuwe tekst moet hebben om een even grote afname in de moeilijkheidsgraad op te leveren.
   

 

Als een tekst herschreven wordt maar S niet verandert, dan moet gelden dat   1,0430 • √(M • 30/Z)  + 3,1291 constant blijft.
       

4p.

3.

Beredeneer, dus zonder gebruik te maken van rekenvoorbeelden, dat hieruit volgt dat dan moet gelden:
Z = constante • M .
   

 

Door een tekst te herschrijven in een tekst met meer zinnen, kun je S kleiner maken. Als we ervan uitgaan dat van een tekst het aantal woorden met drie of meer lettergrepen 75 is en blijft, dan kun je de formule van S herschrijven als

S = 1,0430 • √75 • √30 • Z -0,5  + 3,1291

en dus als

S = 49,47 • Z-0,5 + 3,1291

Die laatste formule kun je vervolgens differentiëren.
       

4p.

4.

Geef de formule van de afgeleide  dS/dZ en leg met behulp van deze afgeleide uit dat S afnemend daalt als de hoeveelheid zinnen groter wordt.
   

 
Tarwe.
       

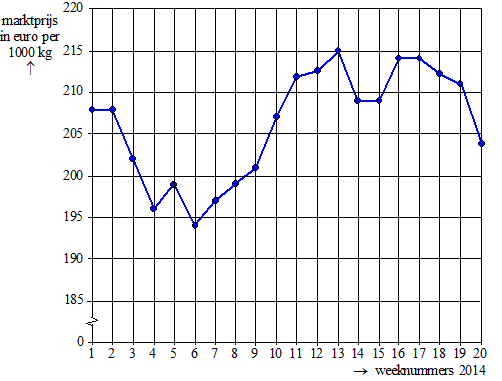
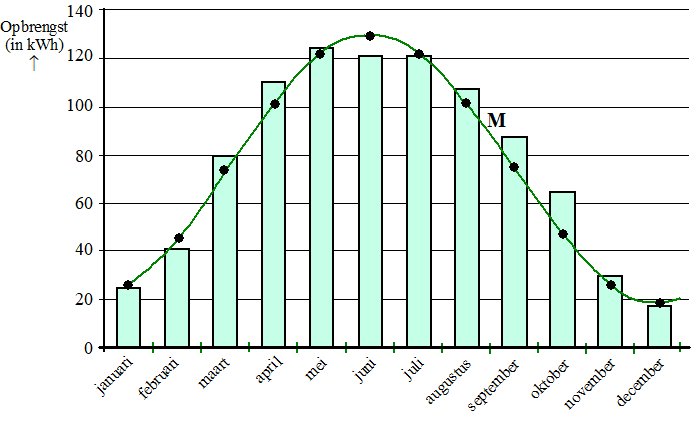
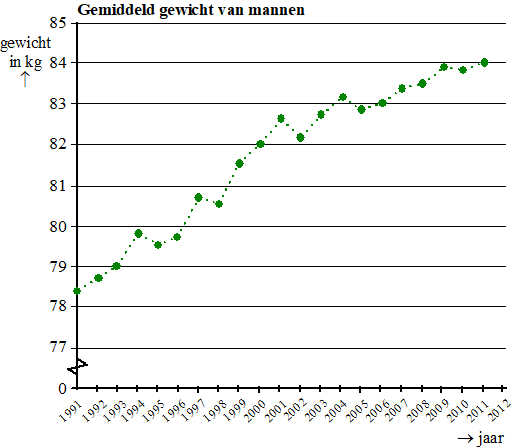
Tarwe is één van de belangrijkste granen. Van tarwe wordt bloem gemalen en brood gemaakt. Aan het begin van iedere week wordt op de groothandelsbeurs van Rotterdam de actuele marktprijs van tarwe (in euro per 1000 kg) bekendgemaakt. Op de site productschapakkerbouw.nl zijn voor de eerste weken van 2014 deze marktprijzen door middel van stippen in een figuur gezet. De stippen zijn met lijnstukjes verbonden. Zie onderstaande figuur.
       

       

In de figuur zie je dat de marktprijs van week 3 naar week 4 gedaald is. Ook van week 13 naar week 14 is een daling te zien.
       

3p.

5.

Beredeneer, zonder berekening, in welk van beide perioden de procentuele daling van de marktprijs van tarwe het grootst is.
     

 

Er is een verband tussen de vraag naar tarwe en de prijs van tarwe. In het boek ‘Wiskunde voor economie’ wordt daarvoor de volgende prijs-vraag-formule vermeld:

       

Hierin is p de prijs in euro per 1000 kg en q de vraag in 1000 kg per maand.
       

3p.

6.

Bereken de grootste gehele waarde van q waarvoor deze prijs-vraag-formule nog betekenis heeft.
     

 

Op een bepaald moment wordt tarwe verhandeld voor 232 euro per 1000 kg.
       

4p.

7.

Bereken, uitgaande van de formule, met hoeveel kg per maand de vraag afneemt als de prijs toeneemt van 232 euro per 1000 kg naar 238 euro per 1000 kg. Rond je antwoord af op tientallen kilo’s.
     

Men kan aantonen dat de totale maandopbrengst een maximale waarde heeft.
       

5p.

8.

Bereken, mede gebruikmakend van de formule, bij welke prijs per 1000 kg die maximale waarde bereikt wordt. Rond je antwoord af op hele euro’s.
     

 
Prille groei
       

Gemiddeld duurt een zwangerschap bij de mens 38 weken. Een ongeboren kind van 8 weken of ouder wordt een foetus genoemd.
In de volgende tabel staat het (gemiddelde) lichaamsgewicht G in gram van een foetus bij een leeftijd van t weken.
       
Leeftijd t in weken Lichaamsgewicht G in gram
8 4,7
10 21
15 160
20 480
25 990
30 1700
35 2700
38 3500
       

In deze opgave willen we onderzoeken welk model er bij deze tabel zou kunnen passen.
Het eerste model dat we bekijken is dat van exponentiële groei:

G = b • at  met a en b constanten.

Veronderstel dat de groei tussen week 8 en week 10 inderdaad exponentieel verloopt.
       

3p.

9.

Bereken met hoeveel procent per week het gewicht van de foetus dan toeneemt in die periode.
     

 

Exponentiële groei is echter geen goed model voor de groei van de foetus in de gehele periode van 8 tot 38 weken. Dit kun je afleiden uit de tabel.
       

3p.

10.

 Laat dat met een berekening zien.
     

 

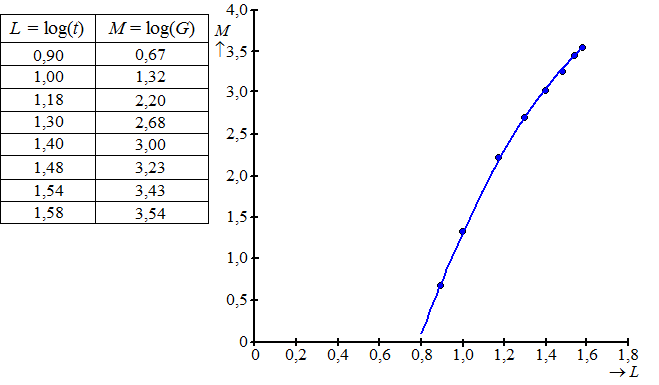
Om een beter model voor de groei van de foetus te maken, berekenen we de logaritmes van de getallen in de vorige tabel.
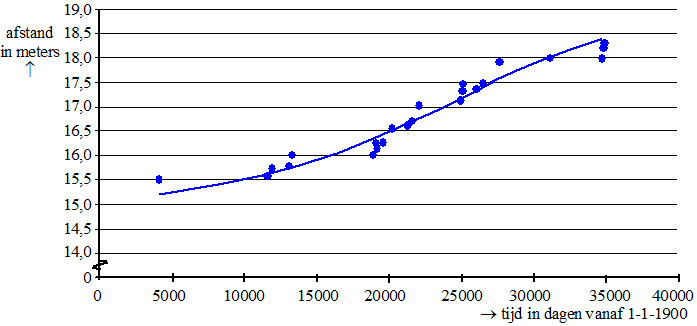
We bekijken dus de waarden van M = log (G) ten opzichte van L = log (t) . Zie de volgende tabel en de bijbehorende punten in de figuur ernaast.
       

       

De punten in de figuur liggen bij benadering op een bergparabool. Deze parabool is in de figuur getekend. Bij deze parabool hoort de volgende formule:

M = −7,131+11,305 • L − 2,892 • L2

Als de parabool van de figuur de groei goed beschrijft, dan zou de grafiek moeten stijgen gedurende de hele zwangerschap.
       

4p.

11.

Bereken met behulp van de afgeleide functie M' de waarde van t waar de grafiek van M weer gaat dalen en leg uit dat dit voor het model geen bezwaar is.
     

 

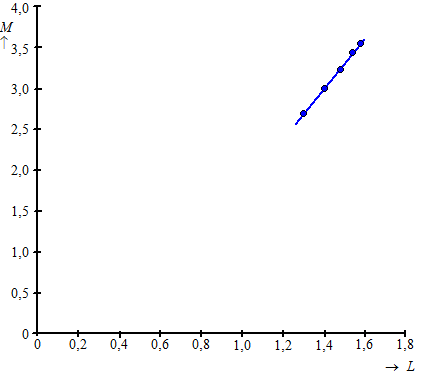
Voor een foetus van 20 weken en ouder blijkt een rechte lijn nog beter bij de punten in de figuur te passen dan de parabool van zojuist. Deze lijn is in onderstaande figuur getekend.
       

       

De vergelijking van deze lijn is:

M = −1,314 + 3,075 • L

Omdat geldt M = log (G) en L = log (t) is deze vergelijking te schrijven als

log(G) = −1,314 + 3,075 • log(t)   (formule 1)

Deze formule 1 is te herschrijven tot formule 2:

G = 0,0485 • t3,075  (formule 2)
       

4p.

12.

Laat zien hoe je formule 1 kunt herleiden tot formule 2 of hoe je formule 2 kunt herleiden tot formule 1.
     

 

 

Zonne-energie.
       

Met zonnepanelen kan elektriciteit geproduceerd worden. De opbrengst van zonnepanelen varieert door het jaar heen: in de zomer is de opbrengst groter dan in de winter.

In de figuur zie je in het staafdiagram de gemiddelde maandopbrengsten van een zonnepanelensysteem bij Leiden. Om de gemiddelde maandopbrengsten te bepalen, worden de maandopbrengsten van de laatste 10 jaren gebruikt. De opbrengst wordt gemeten in kilowattuur (kWh).
       

       

De gemiddelde maandopbrengsten kunnen benaderd worden door een model: zie de kromme M in de figuur. De werkelijke gemiddelde maandopbrengst wijkt relatief het meest af in oktober van de door het model voorspelde waarde.
       

4p.

13.

Licht toe hoe je in de figuur kunt zien dat die relatieve afwijking inderdaad in oktober het grootst is en bereken deze relatieve afwijking.
       

De kromme van de gemiddelde maandopbrengst M in de figuur is een sinusoïde.
       

4p.

14.

Stel een formule op voor M als functie van de tijd t in maanden. Neem hierbij voor januari t =1.
       

Bij een ander zonnepanelensysteem is voor elke dag in het jaar op basis van de gegevens van 10 jaar de gemiddelde dagopbrengst bepaald. De gemiddelde dagopbrengst kan benaderd worden met de formule:

D = 6,34 + 4,19sin(0,0172(t −74))

Hierin is D de gemiddelde dagopbrengst in kWh en t de tijd in dagen met t = 1 op 1 januari.
       

3p.

15.

Bereken op hoeveel dagen per jaar de gemiddelde dagopbrengst volgens deze formule groter is dan 10 kWh.
       
Hink stap sprong
       

Het wereldrecord op het atletieknummer hink-stap-sprong is in de 20e eeuw 24 maal verbeterd. De tabel geeft hiervan een overzicht.
       
30 - 5 - 1911 15,52 m   26 - 3 - 1955 16,56 m   5 - 8 - 1971 17,40 m
27- 10 - 1931 15,58 m 19 - 7 - 1958 16,59 m 17 - 10 - 1972 17,44 m
14 - 8 - 1932 15,72 m 3 - 5 - 1959 16,70 m 15 - 10 - 1975 17,89 m
14 - 12 - 1935 15,78 m 5 - 8 - 1960 17,03 m 16 - 6 - 1985 17,97 m
6 - 8 - 1936 16,00 m 16 - 10 - 1968 17,10 m 18 - 7 - 1995 17,98 m
30 - 9 - 1951 16,01 m 17 - 10 - 1968 17,22 m 7 - 8 - 1995 18,16 m
23 - 7 - 1952 16,12 m 17 - 10 - 1968 17,23 m 7 - 8 - 1995 18,29 m
23 - 7 - 1952 16,22 m 17 - 10 - 1968 17,27 m    
19 - 7 - 1953 16,23 m 17 - 10 - 1968 17,39 m    
       

Het verloop van het wereldrecord in de tijd wordt met stippen weergegeven in de onderstaande figuur.
       

       

Voor het verband tussen tijd t (in dagen sinds 1 januari 1900, dus t = 0 op 1 januari 1900) en het wereldrecord w in meters is door een wiskundige het volgende model opgesteld:
       

       
Ook de grafiek die hoort bij dit model zie je in de bovenstaande figuur.
       

4p.

16.

Bereken met de formule in welk jaar volgens dit model het wereldrecord voor het eerst boven de 18 meter zou komen. Je hoeft hierbij geen rekening met schrikkeljaren te houden.
       

Volgens dit model zal het wereldrecord hink-stap-sprong op den duur naar een grenswaarde naderen.
       

3p.

17.

 Beredeneer met behulp van de formule voor w wat deze grenswaarde is.
       

Een formule voor de afgeleide functie van w is

       

4p.

18.

 Toon dit aan.
       

De afgeleide beschrijft met hoeveel meter het record (theoretisch) per dag stijgt.
       

5p.

19.

Bereken met behulp van de afgeleide in welk jaar het wereldrecord hink-stap-sprong volgens het model het snelst toenam en onderzoek of dit overeenkomt met de werkelijkheid. Je hoeft hierbij geen rekening met schrikkeljaren te houden.
       

Veel mensen meten de tijd liever in jaren dan in dagen. Voor hen stelt de wiskundige een andere formule op, van de vorm
       

       
Hierin is j de tijd in jaren, waarbij j = 0 overeenkomt met 1 januari 1900.
       

3p.

20.

Bepaal de waarde van het getal dat op de puntjes voor j moet staan. Je hoeft hierbij geen rekening met schrikkeljaren te houden.
       
Lengteverschil.
       

Het Centraal Bureau voor de Statistiek schreef in december 2012 het volgende:
       

Nederlanders steeds langer maar vooral dikker

Nederlanders groeien nog steeds, zowel in de lengte als in de breedte.
In de afgelopen twintig jaren is de Nederlander een stuk zwaarder geworden. Het gemiddelde gewicht van vrouwen is vanaf 1991 tot en met 2011 met 3,7 kg toegenomen tot 70 kg. Bij mannen is deze toename aanzienlijk groter.
       

De schrijver van het artikel baseert deze conclusies op berekeningen met de gemiddelde Body Mass Index (GBMI).
De GBMI berekent men met de formule
       

       

Hierbij wordt het gewicht uitgedrukt in kg en de lengte in meters.

In de figuur hieronder staat het gemiddelde gewicht van mannen vanaf 1991. In de tabel vind je de GBMI voor zowel mannen als vrouwen voor de jaren 1991, 1993, 1995, 1997, 1999, 2001, 2003, 2005, 2007, 2009 en 2011.
       

       
tabel GMI
jaar mannen vrouwen
1991 24,5234 23,8013
1993 24,6009 23,8160
1995 24,7014 24,1383
1997 24,8521 24,3890
1999 25,0707 24,5094
2001 25,3247 24,7004
2003 25,4116 24,8133
2005 25,4167 24,8073
2007 25,5135 24,8133
2009 25,6097 24,9440
2011 25,6686 24,9499
       

Met behulp van de gegevens kun je aantonen dat Nederlanders sinds 1991 gemiddeld een stuk langer zijn geworden. Vooral mannen worden steeds langer. Het verschil in gemiddelde lengte tussen mannen en vrouwen neemt nog steeds toe.

Een wetenschapsjournalist beweert: “Als we aannemen dat het lengteverschil vanaf 1991 ieder jaar evenveel toeneemt, zal dit verschil in 2030 al meer dan 16 cm zijn.”
       

8p.

21.

Onderzoek met behulp van de gegevens in het artikel, de figuur en de tabel of deze bewering waar is.
       

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. De tekst bestaat uit drie zinnen, dus Z = 3
S = 1,0430 • √(14 • 30/3) + 3,1291 = 1,0430 • √140 + 3,1291 = 15,47
Afgerond is S = 15
   
2. als M 15% kleiner wordt is de nieuwe M dus gelijk aan 0,85M
Dan staat er onder de wortel  0,85M • 30/Z
Als je Z verandert in X dan staat er onder de wortel   M • 30/X

Die twee moeten gelijk zijn:    0,85M • 30/Z  =   M • 30/X 
0,85/Z = 1/X    geeft   Z = 0,85X  dus  X = 1/0,85 • Z = 1,18Z
Dat is dus 18% meer
   
3. 1,0430 • √(M • 30/Z)  + 3,1291 is constant
dus √(M • 30/Z) is constant
dus M • 30/Z is constant
M • 30/Z = c  geeft  M • Z = c/30 en dat is weer constant.
   
4. S' = -0,5 • 49,47Z-1,5 
S' = -24,735 • Z-1,5
S' = -24,735/Z1,5

Omdat Z > 0  is dit altijd negatief dus is S dalend.
Als Z groter wordt, dan wordt Z1,5 ook groter dus wordt S' kleiner (negatief), en dat betekent dat de daling afneemt, dus dat S afnemend dalend is.
   
5. De daling is in beide perioden gelijk want de lijntjes lopen even steil omlaag
Maar dan is dat in procenten tussen week 3 en 4 in procenten groter want daar is de marktprijs lager.
   
6. De formule heeft betekenis zolang het deel onder de wortel groter dan nul is.
-23q + 3800 = 0
23q = 3800
q = 165,22
   
7. 232 = 10√(-23q + 3800)
23,2 = √(-23q + 3800)
538,24 = -23q + 3800
23q = 3261,76
q = 141,8157

238 = 10√(-23q + 3800)
23,8 = √(-23q + 3800)
566,44 = -23q + 3800
23q = 3233,56
q = 140,5896

Dat is een afname van 1,2261 duizend kilo, dus ongeveer 1230 kg 
   
8. O = p • q = p • 10 • √(-23q + 3800)
Plot de grafiek van Y1 = X * 10 * √(-23X + 3800)
calc - maximum geeft   (q = 110 en) O = 356.
   
9. in twee weken is de groeifactor  21/4,7 = 4,468
voor de g per week geldt dus  g2 = 4,468  dus  g = 4,4680,5 = 2,11
dat is een toename van 111% per week
   
10. bijvoorbeeld:
tussen week 10 en 15 is de groeifactor  160/21 = 7,62
tussen week 30 en 35 is de groeifactor 2700/1700 = 1,59
Dat is niet gelijk, terwijl de tijdsverschillen wel gelijk zijn (5 weken) dus de groei is niet exponentieel.
   
11. de grafiek gaat weer dalen als M' = 0
M' =  11,305 - 5,784 • L = 0
5,784L =  11,305
L = 1,95
Dan is  log(t) = 1,95  dus  t = 101,95 ≈ 89  weken.
Maar zo lang duurt een zwangerschap nooit.
   
12. van 1 naar 2:
log(G)( = -1,314 + 3,075  log(t)
10log(G) = 10-1,314 + 3,075log(t)
G = 10-1,314 • 103,075log(t)
G = 0,0485 • (10log(t))3,075 
G =  0,0485 • t3,075  

van 2 naar 1:
G = 0,0485 • t3,075
log(G) = log(0,0485 • t3,075)
log(G) = log(0,0485) + log(t3,075)
log(G) = -1,314 + 3,075 • log(t)
   
13. In oktober is het verschil het grootst en in de maanden met een kleiner totaal  (jan, feb, nov, dec)  is het verschil alleen maar kleiner. Dus is het relatieve verschil in oktober het grootst.

Het verschil is ongeveer 765 - 48 = 17
Het totaal in oktober is 48
Dat is dus  17/48 • 100% = 35% hoger.
   
14. Het maximum is 130 en het minimum is 19
De evenwichtlijn is dan   (130 + 19)/2 = 74,5
De amplitude is dan  130 - 74,5 = 55,5
De periode is 12 maanden dus in de formule, staat 2π/12 = 0,52
De sinus gaat door de evenwichtslijn omhoog bij t = 3
Dat geeft   M = 74,5 + 55,5 sin(0,52(t - 3))
   
15. 6,34 + 4,19sin(0,0172(t −74)) = 10
Y1 = 6,34 + 4,19 * sin(0,0172(X - 74)
Y2 = 10
GR op Rad.
Intersect geeft  t = 135,9  en t = 194,9
Dat is dus vanaf dag 136 tm dag 194 en dat zijn 59 dagen.
   
16. Y1 = 15 + 4/(1 + 36*e^(-0,00015X))
Y2 = 18
intersect geeft t = 31215 dus dat is 31215/360 = 85,5 jaar vanaf 1 januari 1900
Dat is in  1985.
   
17. Als t oneindig groot wordt, dan wordt e-0,00015t  bijna nul
Dus staat er in de  noemer van de breuk o0ngeveer 1
dan is w ≈ 15 + 4/1 = 19 meter,  dus dat is de grenswaarde.
   
18. quotiëntregel:
 
  4 • 36 • 0,00015 is inderdaad gelijk aan 0,0216
   
19. Plot de grafiek van  w'  en kijk wanneer die een maximum heeft.
calc - maximum geeft  t = 23890
23890/365 = 65,4 jaar na 1 jan 1900,   dus dat was in 1965
Dat klopt niet met de werkelijkheid want van 1960 naar 1968 steeg het record maar 7 cm in 8 jaar, terwijl in 1968 het al binnen een jaar 22 cm steeg.
   
20. t = 365j
dus -0,00015t wordt  -0,00015 • 365t = -0,05475t
   
21. 1991:  vrouwen: 
G = 66,3 (tekst) en GBMI = 23,8013 (tabel)  dus  L = √(G/B) = 1,6690 m
1991 mannen:
G = 78,4 (grafiek) en GBMI = 24,5234 (tabel)  dus L = √(G/B) = 1,788 m
het verschil in 1991 is 0,119 m

2011 vrouwen:
G = 70,0 (tekst) en GBMI = 24,9499 (tabel) dus L = √(G/B) = 1,6750 m
2011 mannen:
G = 84,0 (grafiek) en GBMI = 25,6686 (tabel) dus  L = √(G/B) = 1,8090 m
het verschil in 2001 is 0,134 m

Het verschil is in 20 jaar toegenomen van 0,119 m naar 0,134 m  en dat is 0,015 m = 1,5 cm.
Per jaar is dat 0,075 cm
2030 is over 19 jaar dus zal het verschil nog 19 • 0,075 = 1,425 cm zijn toegenomen
Dan is het verschil 13,4 + 1,425 = 14,825 cm

Dat is niet meer dan 16 cm dus de uitspraak klopt niet.