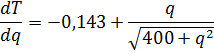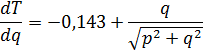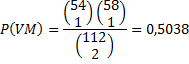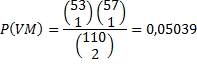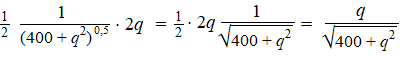VWO WA, 2016 - I

 

Aalscholvers en vis
       

In het IJsselmeergebied leven veel aalscholvers. Deze vogels voeden zich met vis. Zij zijn daarom een concurrent voor de visserij in het IJsselmeergebied.
In de periode 1997-2001 is uitgebreid onderzoek gedaan naar de visconsumptie van aalscholvers. Hiervoor werden braakballen van aalscholvers geanalyseerd.

Uit het braakballenonderzoek bleek dat een volwassen aalscholver ongeveer 360 gram vis per dag at en een jong ongeveer 285 gram per dag.
In juni 1999 zijn er in het IJsselmeergebied 30012 volwassen en 6961 jonge aalscholvers geteld. We gaan ervan uit dat die aantallen voor de gehele maand golden.
       
3p.

1.

Bereken hoeveel kg vis er in die maand door de aalscholvers gegeten is. Rond je antwoord af op duizendtallen.
     

 

Eén keer per dag braakt een  aalscholver een bal uit met alle onverteerbare resten van de vissen die hij die dag gegeten heeft. In zo'n braakbal zitten onder andere otolieten (gehoorsteentjes) en kauwplaatjes van verschillende vissoorten (zie foto). Deze worden gesorteerd op vissoort en de lengtes worden gemeten.

Met behulp van formules kan men dan de lengte en het gewicht berekenen van de vissen waarvan ze afkomstig zijn. Zo wordt vastgesteld wat de aalscholver die dag gegeten heeft. In de tabel staan de gebruikte formules voor twee belangrijke vissoorten die op het menu staan van de aalscholver.

       
vissoort formule voor de lengte formule voor het gewicht
pos L = -11,31+ 22,14 ·O log(G) = -5,607 + 3,335· log(L)
blankvoorn log(L) =1,692 + 0,734· log(K) log(G) = -5,833 + 3,396 · log(L)
       

In deze formules is O de gemeten otolietlengte in mm, K de gemeten kauwplaatlengte in mm, L de lengte van de vis in mm en G het gewicht van de vis in gram.

In een braakbal wordt een otoliet van een pos aangetroffen. Deze otoliet heeft een lengte van 3,4 mm.
       
4p.

2.

Bereken het gewicht van deze pos. Geef je antwoord in gram in één decimaal nauwkeurig
     

 

Voor de blankvoorn kunnen we de twee formules in de tabel herleiden tot één formule waarmee we het gewicht van deze vis uit de kauwplaatlengte kunnen berekenen.
Deze formule heeft de vorm: log(G) = a + b · log(K).
       
3p.

3.

Bereken de waarden van a en b in deze formule. Geef je antwoorden in drie decimalen nauwkeurig.
     

 

Bij de blankvoorn is het verband tussen kauwplaatlengte en de lengte van de vis in de tabel anders te schrijven: de formule log(L) = 1,692 + 0,734 · log(K) is te herleiden tot

L = 49,2 · K0,734

Aan de exponent 0,734 in deze formule kunnen we zien dat de lengte van de vis steeds minder sterk toeneemt bij toenemende kauwplaatlengte. Dat kun je ook met behulp van de afgeleide nagaan.
       
4p.

4.

Stel een formule op voor de afgeleide van L en laat met behulp hiervan zien dat L afnemend stijgend is.
     

  
Sociale psychologie
       

Psychologen denken dat een man door een gesprek met een mooie vrouw zo afgeleid kan zijn dat daardoor zijn denk- en leerprestaties na het gesprek tijdelijk verminderen. De afdeling sociale psychologie van de Radboud Universiteit Nijmegen onderzocht dit verschijnsel in 2009  (Het hier genoemde onderzoek had alleen betrekking op heteroseksuelen.). Deze opgave gaat over enkele experimenten die daarbij werden gebruikt.

Eerste experiment: de 2-back-taak
In het eerste experiment moest een aantal mannelijke proefpersonen een test op de computer doen. Deze test was een zogenoemde 2-back-taak: op het scherm verschijnt met tussenpozen steeds een willekeurig gekozen letter van het alfabet. De proefpersoon moet deze letter onthouden en vergelijken met de letter twee stappen later. Als de letters hetzelfde zijn, moet hij de linkertoets indrukken, anders de rechtertoets. Zie het voorbeeld in de volgende tabel.
       
letter T B N D W D A P P Q F Q ...
toets: li = links,  re = rechts ... ... re re re li re re re re re li ...
       

De proefpersoon moet voor een 2-back-taak 200 keer een toets indrukken
       
4p.

5.

Bereken de kans dat de proefpersoon in dat geval meer dan 10 keer de linkertoets moet indrukken.
     

 

Na deze test hadden de (mannelijke) proefpersonen een kort gesprek met een mannelijke onderzoeker of een vrouwelijke onderzoeker. Hierna moesten ze opnieuw een 2-back-taak doen. Nu werd er niet gekeken naar het aantal goede antwoorden maar naar de reactietijd bij de goede antwoorden. De (mannelijke) proefpersonen die een gesprek hadden gehad met een vrouw scoorden op deze test aanzienlijk minder goed dan degenen die met een man gesproken hadden. In de volgende tabel  zie je voor beide groepen de resultaten van deze laatste test.
       
gesprek met reactietijd van mannen in milleseconde
gemiddelde standaardafwijking
vrouw 1436 663
man 1255 589
       

We veronderstellen dat de reactietijden van beide groepen normaal verdeeld zijn.
       
3p.

6.

Bereken de kans dat een willekeurig gekozen man uit de groep die een gesprek had met een vrouw beter scoorde dan het gemiddelde van de groep die een gesprek had met een man.
     

 

Tweede experiment
In een tweede experiment was een groep van 112 proefpersonen betrokken, bestaande uit 54 mannelijke en 58 vrouwelijke willekeurig gekozen studenten. Voor dit experiment werden tweetallen gevormd.

Veronderstel dat van deze personen er steeds willekeurig twee aan elkaar gekoppeld werden, zonder erop te letten of de persoon een man of vrouw is.
       
5p.

7

Bereken de kans dat de eerste twee tweetallen die zo gevormd werden allebei uit een man en een vrouw bestonden. Rond je antwoord af op vier decimalen.
     

 

De proefpersonen van elk tweetal moesten met elkaar een gesprek van 5 minuten voeren. Na dit gesprek moesten ze individueel een test doen. Ook hier werd gekeken naar de gemiddelde reactietijd bij de goede antwoorden.

Op grond van eerder onderzoek mogen we aannemen dat de reactietijd van mannen in het algemeen na zo'n gesprek normaal verdeeld is met een gemiddelde van 594 milliseconde en een standaardafwijking van 53 milliseconde.

Zoals al eerder vermeld, vermoeden psychologen dat mannen die een gesprek met een vrouw gevoerd hebben, gemiddeld een langere reactietijd hebben. De 22 mannen in dit onderzoek die een gesprek met een vrouw gevoerd hadden, bleken een gemiddelde reactietijd van 631 milliseconde te hebben.
       
4p.

8.

Bereken, uitgaande van de genoemde normale verdeling, de kans dat de gemiddelde reactietijd van een groep van 22 willekeurig gekozen mannen 631 milliseconde of meer is.
     

  
Fietsen en energie.
       

De formules voor het basisenergieverbruik, de energie die iemand per dag nodig heeft voor alle activiteiten van een lichaam in rust, zoals hartwerking, ademhaling, enzovoort, staan in tabel 1. In deze formules is B het basisenergieverbruik in kcal (kilocalorieën) per dag en G het lichaamsgewicht van de persoon in kg.
       
Tabel 1:  basisenergieverbruik
leeftijdsgroep formule
18 - 30 jaar (jongvolwassen) B = 15,3G + 679
31 - 60 jaar (ouder) B = 11,6G + 879
       

Er gelden verschillende formules voor jongvolwassen en voor oudere personen. We vragen ons af welke van deze twee groepen het laagste basisenergieverbruik heeft. Dit hangt volgens de formules in tabel 1 af van het lichaamsgewicht van een persoon.
       
4p.

9.

 Onderzoek bij welke lichaamsgewichten tussen 40 en 120 kg de jongvolwassenen een lager basisenergieverbruik hebben dan de ouderen.
     

 

Als iemand sport, is de totale energie die hij of zij nodig heeft groter dan het basisenergieverbruik. De formule voor de totale energie T per dag is T = 1,3B + S. Hierbij is B het basisenergieverbruik per dag en S het energieverbruik voor het sporten per dag zoals fietsen, zwemmen en hardlopen.

In tabel 2 staat het energieverbruik in kcal per kg lichaamsgewicht per uur bij fietsen bij een aantal snelheden. Neem aan dat het energieverbruik tussen de aangegeven snelheden in lineair verloopt.
       
Tabel 2:  energieverbruik bij fietsen
snelheid (km/uur) 14 17 20 24 28 35 42
energieverbruik
(kcal/kg/uur)		 4 6 8 10 12 16 20
       

Frits is 58 jaar en weegt 70 kg. Hij doet mee aan de fietselfstedentocht in Friesland, een tocht waarbij op één dag 240 km gefietst wordt. We nemen aan dat hij de hele tocht rijdt met een snelheid van 25 km/uur.
       
4p.

10.

 Bereken het totale energieverbruik van Frits op deze dag.
     

 

Bij een hogere snelheid wordt per uur een grotere afstand afgelegd. Je kunt voor elke snelheid die in de tabel  vermeld wordt, het energieverbruik per kg lichaamsgewicht bij het fietsen per afgelegde kilometer berekenen. Alex beweert dat dit voor elke snelheid gelijk is. Bert zegt dat dit hoger is bij hogere snelheden en Carolien beweert dat dit lager is bij hogere snelheden. Eén van deze drie personen heeft gelijk.
       
4p.

11.

 Onderzoek met behulp van tabel 2 wie van de drie gelijk heeft.
     

 

Bij een triatlon wordt er achtereenvolgens gezwommen, gefietst en hardgelopen. Er zijn veel verschillende afstanden mogelijk voor de drie onderdelen. Zo bestaat de Ironman − ook wel de hele triatlon genoemd − uit een zwemonderdeel van 3800 m, een fietsonderdeel van 180 km en een hardlooponderdeel van 42,2 km. De Olympische triatlon echter, gaat over 1500 m zwemmen, 40 km fietsen en 10 km hardlopen.

Je zou een triatlon kunnen samenstellen waarbij voor elk onderdeel het energieverbruik voor het sporten even groot is. We gaan daarbij uit van een atleet die met een dusdanige snelheid hardloopt, dat zijn energieverbruik 1 kcal per afgelegde kilometer is. De atleet zwemt met een snelheid waarbij zijn energieverbruik 4 kcal per km is. En hij fietst met een snelheid waarbij hij 0,4 kcal per km verbruikt. De genoemde waarden voor het energieverbruik gelden steeds per kg lichaamsgewicht.
       
5p.

12.

Bereken de afstanden voor het zwemmen, fietsen en hardlopen in een triatlon van in totaal 21 km waarbij het energieverbruik van deze atleet voor elk onderdeel steeds even groot is.
     

  

 

Elvis
       

De Amerikaan T.J. Pennings heeft onderzocht hoe snel zijn hond Elvis een weggegooide bal bereikt. In onderstaande figuur staat een schets van het bovenaanzicht van de situatie. Pennings en Elvis staan bij het vaste punt A. Het vaste punt C bevindt zich 15 meter verderop langs de waterkant. Pennings gooit een bal in het water, zodanig dat deze ergens op de denkbeeldige lijn door C loodrecht op de waterkant terechtkomt; het punt waar de bal terechtkomt, noemen we B. De afstand BC, uitgedrukt in meters, noemen we p.
       

       

Elvis bepaalt zelf het punt vanaf waar hij gaat zwemmen. Dat punt noemen we D. Dus Elvis rent van A naar D langs de waterkant en zwemt vervolgens van D naar B.
Pennings doet dit experiment 35 keer (eigenlijk gooide Pennings wel vaker dan 35 keer, maar alle keren waarbij hij er niet in slaagde om de bal ter hoogte van C te gooien, schrapte hij uit zijn waarnemingen), waarbij hij de afstand p steeds varieert. Bij elke worp noteert hij p en de afstand CD. Deze afstand CD, uitgedrukt in meters, noemen we q. De waarden van p en q heeft Pennings uitgezet in de figuur hieronder: elk punt hoort bij een worp.
       

       

Zo lees je af dat bij een van de worpen geldt: p = 15,3 en q = 2,3 (zie punt E). Dat betekent dat Elvis 2,3 meter voor punt C in het water springt.
Uit de figuur blijkt dat de punten bij benadering op een rechte lijn door (0,0) liggen. Dat betekent dat q recht evenredig is met p.
Op basis van deze recht evenredigheid kan men de volgende conclusies trekken:
 
1.

Hoe verder van punt C de bal in het water komt, hoe eerder Elvis het water in springt.
2.

Als de afstand CB twee keer zo klein wordt, wordt de afstand AD ook twee keer zo klein.
       

4p.

13.

Geef van elk van de beide bovenstaande conclusies aan of deze volgt uit het recht evenredige verband. Licht je antwoord toe.
     

 

De vergelijking van de rechte lijn uit de figuur is bij benadering q = 0,2 • p. Hierin is de richtingscoëfficiënt 0,2 een grove benadering.
       

3p.

14.

Bereken de waarde van de richtingscoëfficiënt van deze lijn in twee decimalen nauwkeurig met behulp van de figuur.
     

 

Het is ook mogelijk het gedrag van Elvis theoretisch te bekijken. Hierover gaat de rest van deze opgave.

De afstand AC is 15 meter en de afstand BD is volgens de stelling van Pythagoras gelijk aan  √(p2 + q2).

We nemen bovendien aan dat Elvis met een constante snelheid van 7 m/s rent en met een constante snelheid van 1 m/s zwemt. In de figuur zie je voor punt E dat p =15,3 en q = 2,3.

       

5p.

15.

Bereken met deze gegevens de totale tijd die Elvis nodig heeft om de bal te bereiken bij de worp die bij punt E hoort.
     

 

Voor elke worp kunnen we de totale tijd die Elvis nodig heeft om de bal te bereiken, berekenen met de formule:

T = 0,143 • (15 - q) + √(p2 + q2).

Hierin is T de totale tijd in seconden en q de afstand CD in meters.
Voor de volgende vraag bekijken we een worp waarbij de afstand CB = 20m, dus p = 20 . De formule wordt dan:

T = 0,143 • (15 - q) + √(400 + q2).
 
De afgeleide van deze formule is:

       

5p.

16.

Toon met behulp van differentiëren aan dat deze afgeleide juist is en bereken door deze afgeleide gelijk aan 0 te stellen, na hoeveel meter rennen Elvis het water in moet springen om zo snel mogelijk de bal te bereiken.
     

 

We gaan nu weer uit van de formule  T = 0,143 • (15 - q) + √(p2 + q2)   en we  bekijken  dT/dq
Er geldt:
       

       

4p.

17.

Laat zien dat door deze afgeleide gelijk aan 0 te stellen de vergelijking q = 0,14p ontstaat, waarbij 0,14 is afgerond op twee decimalen.
     

  

 

Huizenprijzen.
       

In dagblad Trouw van 22 augustus 2012 stond bij een artikel over de daling van de gemiddelde huizenprijs de onderstaande figuur.
       

       

In deze figuur is de verandering in prijs van verkochte koopwoningen in Nederland weergegeven in procenten ten opzichte van dezelfde maand een jaar eerder. Je kunt bijvoorbeeld aflezen dat de huizenprijs in oktober 2008 gemiddeld 2,3% hoger was dan in oktober 2007. Ook kun je zien dat de huizenprijs in oktober 2009 gemiddeld 5,2% lager was dan in oktober 2008.

De huizenprijs in februari 2012 is ten opzichte van februari 2009 met ongeveer 8,8% gedaald.
       

4p.

18.

Bereken met behulp van de figuur deze daling in procenten in twee decimalen nauwkeurig.
     

 

In de figuur kun je aflezen dat de huizenprijs in april 2010 gedaald is ten opzichte van april 2009. Je kunt echter niet aflezen of de huizenprijs in april 2010 gedaald is ten opzichte van de voorgaande maand (maart 2010).

Met behulp van indexcijfers kunnen we wel dergelijke conclusies trekken. In de tabel staan de indexcijfers voor maart en april 2009. Bij deze indexcijfers is de huizenprijs in januari 2005 op 100 gesteld en de huizenprijs in een bepaalde maand wordt uitgedrukt als percentage van die huizenprijs in januari 2005.
       
indexcijfers huizenprijs 2009
maart april
110,1 109,5
       

4p.

19.

Onderzoek met behulp van de tabel en de figuur of de huizenprijs in april 2010 gedaald is ten opzichte van maart 2010.
     

 

Dalende huizenprijzen zijn niet alleen vervelend voor huizenbezitters, maar ook voor banken. Banken hebben namelijk vaak geld uitgeleend aan huizenbezitters in de vorm van hypotheken. Als iemand een dergelijke lening niet meer kan terugbetalen, verkoopt de bank het huis. Als de huizenprijzen gedaald zijn, is dat huis echter minder waard dan toen de lening afgesloten werd.

Om de waarde van een huis waarvoor een bank geld heeft uitgeleend te berekenen, gaat de bank uit van de laatste verkoopprijs van dat huis en berekent met behulp van indexcijfers steeds de huidige waarde, de zogenoemde berekende waarde.

Eens in de drie jaar moet getoetst worden of de berekende waarden van de huizen in het bestand van de bank kloppen.

De Nederlandsche Bank schrijft hiervoor de volgende procedure voor:
 
-

De bank moet uit haar bestand een aselecte steekproef nemen van minstens 100 huizen. Deze huizen worden getaxeerd: dit levert de getaxeerde waarde.
-

De bank berekent van elk huis in de steekproef de verhouding Q tussen de berekende waarde en de getaxeerde waarde. In formulevorm:
 

-

De bank toetst met behulp van deze steekproef of de gemiddelde waarde van Q voor de huizen in haar bestand significant lager is dan 1.
       

Deze procedure is ingevoerd om met een grote mate van zekerheid vast te stellen dat een bank de waarde van de huizen in haar bestand niet overschat.
       

2p.

20.

Leg met behulp van de formule voor Q uit waarom de bank de waarde van de huizen in haar bestand zou overschatten als de gemiddelde waarde van Q hoger zou zijn dan 1.
     

 

Om te toetsen of de gemiddelde waarde van Q lager is dan 1 moet er eenzijdig getoetst worden met een significantieniveau van 1%. Neem op grond van ervaringen uit het verleden aan dat Q normaal verdeeld is met standaardafwijking 0,35. Voor de nulhypothese H0 geldt dan μ = 1 en voor de alternatieve hypothese H1 geldt μ < 1.

In een steekproef van 100 huizen wordt de waarde van Q bepaald. Het steekproefgemiddelde blijkt 0,94 te zijn.
       

5p.

21.

Onderzoek of dit resultaat voldoende aanleiding geeft om te concluderen dat de gemiddelde waarde van Q significant lager is dan 1.
     

 

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. Per dag:
door de volwassenen  360 • 30012 = 10804320 gram
door de jongen:  285 • 6961 = 1983885
samen is dat 12788205 gram

Juni heeft 30 dagen dus in de hele maand  30 • 12788205 = 383646150 gram = 383646,150 kg
Op duizenden afgerond is dat 384000 kg. 
   
2. L = -11,31+ 22,14 · 3,4  =  63,966 mm
log(G) = -5,607 + 3,335· log(63,966) = 0,41584......
Dan is  G = 100,41584....  = 2,605... gram en dat is afgerond  2,6 gram
   
3. log(G) = -5,833 + 3,396 · log(L)
log(G) =  -5,833 + 3,396 • (1,692 + 0,734· log(K))
log(G) = -5,833 + 3,396 • 1,692 + 3,396 • 0,734 • log(K)
log(G) = -5,833 + 5,746032 + 2,492664 • log(K)
log(G) = -0,086968 + 2,492664 • log(K)
Dus  a = -0,087  en  b = 2,493
   
4. L = 49,2 · K0,734
L ' = 0,734 • 49,2 • K-0,266   = 36,1128/K0,266
L '  is groter dan nul, dus L is stijgend.
Als K groter wordt, wordt de noemer van L'   groter, dus wordt L'  kleiner, dus stijgt L minder snel.
Dus als K groter wordt, stijgt L minder snel, dus L is afnemend stijgend.
   
5. De kans op de linkertoets is elke keer 1/26.
Dit is dus een binomiaal experiment met n = 200 en p = 1/26
P(meer dan 10) = P(X > 10) = 1 - P(X ≤ 10) =  1 - binomcdf(200,  1/26, 10) = 0,1506.
   
6. Beter scoren betekent een kleinere gemiddelde reactietijd.
Dat betekent een reactietijd kleiner dan 1255.
De kans daarop is  normalcdf(0, 1255, 1436, 663) = 0,3773.
 (met  normalcdf(-1099, 1255, 1436, 663)  krijg je trouwens 0,3924,  maar een reactietijd onder de nul lijkt mij nogal onmogelijk).
   
7.

Eerste tweetal:
 
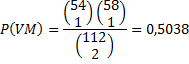
  Dan zijn er nog 53 mannen en 57 vrouwen over, dus voor het tweede tweetal geldt:
 

 
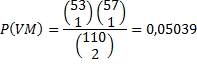  Als beiden moet gebeuren is de kans  0,5038 • 0,5039 = 0,254.

OF

P(MVMV) + P(MVVM) + P(VMVM) + P(VMMV)
= 54/112 • 58/111 • 53/110 • 57/109  +  54/112 • 58/111 • 57/110 • 53/109 +  58/112 • 54/111 • 57/110 • 53/109 + 58/112 • 54/111 • 53/110 • 57/109 = 0,254
   
8. Voor het gemiddelde van een groep van 22 geldt:   μ22 = μ = 594
Voor de standaarddeviatie van het gemiddelde van een groep van 22 geldt  σ22 = σ/√n = 53/√22 = 11,30  
P(631 of meer) =  normalcdf(631, 1099 , 594, 11.30) = 0,00053.
   
9. Wanneer zijn de verbruiken gelijk:
15,3G + 679 = 11,6G + 879
3,7G = 200
G = 200/3,7 = 54,1
De jongvolwassenen hebben bij lagere lichaamsgewichten een kleiner verbruik dan de ouderen
Dat is dus bij gewichten tussen de 40 en 54,1 kg.
   
10. B = 11,6G + 879 = 11,6 • 70 + 879 = 1691 kcal is zijn basisverbruik
240 km met 25 km/uur gemiddeld betekent dat hij  240/25 = 9,6 uur fietst
tussen 24 en 28 neemt het energieverbruik toe met 2 kcal/kg/uur
dus tussen 24 en 25 neemt het toe met 1/4 • 2 = 0,5 kcal/kg/uur
dus bij 25 km/uur is het verbruik  10,5 kcal/kg/uur
T = 1,3 • 1691 + 10,5 • 9,6 • 70 = 9254,3 kcal.
   
11. bekijk één uur, dan is de afstand in km gelijk aan de snelheid:
 
snelheid = afstand 14 17 20 24 28 35 42
energieverbruik 4 6 8 10 12 16 20
energieverbruik per km 0,29 0,35 0,4 0,42 0,43 0,46 0,48
  de laatste rij is gemaakt door het energieverbruik te delen door de afstand.
Je ziet dat het verbruik per km bij hogere snelheden groter wordt, dus Bert heeft gelijk.
   
12. Als je F kilometer fietst en  Z zwemt en H hardloopt, dan verbruik je daarbij  0,4F en 4Z en  H  kcal.
Samen moet dat 21 zijn, dus H + F + Z = 21
H = 4Z  dus  Z = 0,25H
H = 0,4F dus F = 2,5H
Dan staat er  H + 2,5H + 0,25H = 21
3,75H = 21
H = 5,6 km
dan is  F = 14 km en  Z = 1,4 km.
   
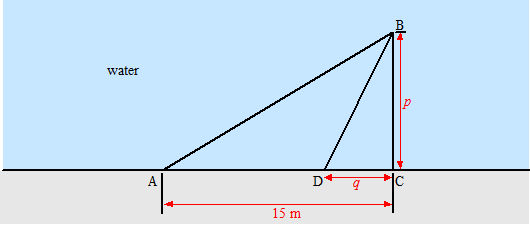
13. 1 volgt WEL uit het recht evenredige verband, immers als p groter wordt, wordt q ook groter.
2 volgt NIET uit het recht evenredige verband, immers als p twee keer zo klein wordt, wordt q dat ook  (recht evenredige verband)  maar dan wordt AD = 15 - q juist groter.
   
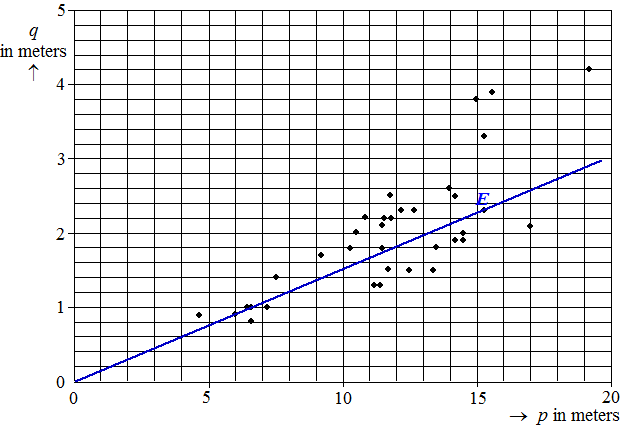
14. De lijn gaat bijvoorbeeld door (14.5, 2.2)
2,2 = a • 14,5  geeft  a = 2,2/14,5 = 0,15
   
15. rentijd:   afstand 15 - q = 12,7 en  snelheid 7 geeft tijd  12,7/7 = 1,8143 seconden
zwemtijd:  √(p2 + q2) = √239,38 = 15,472  en snelheid 1 geeft tijd  15,472 seconden
de totale tijd is dan 1,8143 + 15,472 = 17,28 seconden
   
16. T = 0,143 • 15 - 0,143q + (400 + q2)0,5
0,143  15 heeft afgeleide 0
-0,143q heeft afgeleide -0,143
(400 + q2)0,5  heeft afgeleide  0,5 • (400 + q2)-0,5 • 2q     (die laatste 2q komt van de kettingregel)
   
   
 
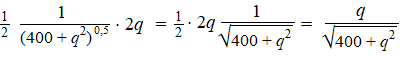  samen met 0 en -0,143 (afgeleide van het eerste deel) geeft dat de gevraagde formule.
   
17.

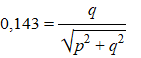  0,143 • √(p2 + q2) = q
kwadrateren:  0,020449(p2 + q2) = q2
0,020449p2 + 0,020449q2 = q2
0,02044p2 = q2 - 0,020449q2
0,020449p2 = 0,979551q2
0,020449/0,979551 • p2 = q2
0,020876 • p2 =  q2
wortel trekken:  0,14448 • p = q
dat is inderdaad ongeveer  q = 0,14p
   
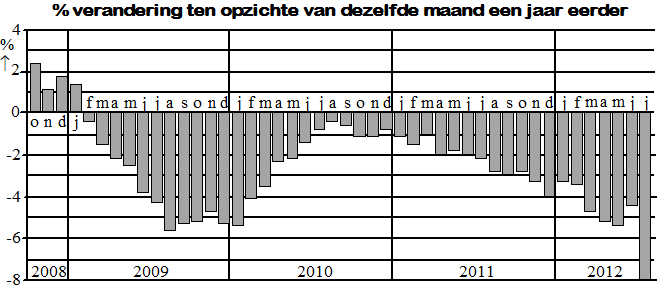
18. aflezen in de figuur: 
februari 2010:  -4,1%  en dat is een vermenigvuldiging met 0,959
februari 2011:  -1,5%  en dat is een vermenigvuldiging met 0,985
februari 2012:  -3,4%  en dat is een vermenigvuldiging met  0,966
samen is dat een vermenigvuldiging met  0,959 • 0,985 • 0,966 = 0,9125
Dat is een daling van  8,75%
   
19. april 2009:  109,5
april 2010 daling van 2,3%  dus vermenigvuldiging met 0,977
april 2010 wordt dan  109,5 • 0,977 = 106,98

maart 2009:  110,1
maart 2010 daling van 3,5% dus vermenigvuldiging met 0,965
maart 2010 wordt dan  110,1 • 0,965 = 106,24

april 2010 is dus NIET gedaald ten opzichte van maart 2010 (maar juist gestegen)
   
20. Als Q groter dan 1 is, dan is de teller groter dan de noemer.
Dus is de berekende waarde groter dan de getaxeerde waarde
Dus de bank overschat de waarde
   
21. H0:  μ = 1  met  σ = 0,35
voor een steekproefgemiddelde van 100 huizen wordt dat:
H0:  μ = 1 met σ = 0,35/√100 = 0,035
overschrijdingskans :  P(X ≤ 0,94)  =  normalcdf(0, 0.94, 1, 0.035) = 0,0432
dat is groter dan het significantieniveau van 0,01
Dus H0 wordt niet verworpen.
Er is dus GEEN aanleiding om de concluderen dat Q van de bank lager is dan 1.