VWO WA, 2015 - I  PILOT
Piramiden.
       
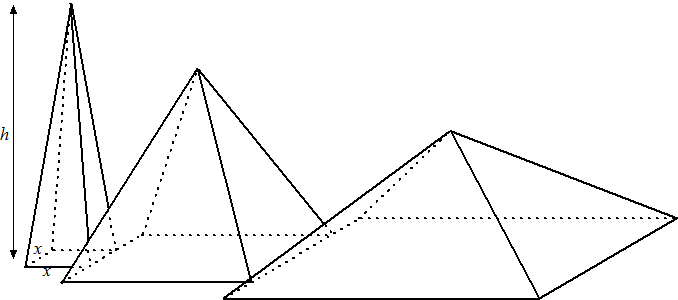
Een kunstenaar ontwerpt een kunstwerk. Hij wil een serie piramiden maken, elk met een vierkant grondvlak. Hij wil dat het grondvlak van de opeenvolgende piramiden steeds groter wordt en de hoogte steeds kleiner. In onderstaande figuur zie je de eerste drie piramiden van een mogelijk ontwerp.
       

       
De kunstenaar gaat de piramiden uitvoeren in beton. Hij moet dus weten hoeveel beton hij nodig heeft. Daarom rekent hij met de formule voor de inhoud van een piramide. De zijde van het vierkante grondvlak, uitgedrukt in dm, noemt hij x. De hoogte van een piramide in dm noemt hij h. Zie de figuur.
De kunstenaar kiest voor een lineair verband tussen h en x en daarvoor gebruikt hij de volgende formule:  h = 9 - ax. Omdat hij nog niet wil vastleggen hoe snel de hoogte afneemt, gebruikt hij de letter a in deze formule.
Voor de inhoud van een piramide geldt de volgende formule:    I = 1/3 • oppervlakte grondvlak • hoogte
In eerste instantie neemt de kunstenaar a = 1.
       
3p. 1. Bereken in die situatie de inhoud van zo’n piramide met een grondvlak van 2,5 bij 2,5 dm.
     

  
Als de waarde van a nog niet gekozen is, geldt voor de inhoud van zo’n piramide de volgende formule:
   
  I  =  1/3 x2 (9 - ax)
 
Hierin is I de inhoud in dm3 en x de lengte van de zijde van het grondvlak in dm.
Als de kunstenaar eenmaal een waarde voor a gekozen heeft, liggen de afmetingen en dus de inhoud van de piramide nog niet vast. Als x verandert, verandert ook de inhoud I.
Neem voor de volgende vraag weer a = 1.
       
4p. 2. Toon met behulp van differentiëren aan dat de inhoud van zo’n piramide dan maximaal is voor x = 6.
     

  
De kunstenaar maakt een nieuw ontwerp. Hij wil de breedte van het grondvlak van de piramiden constant houden en zowel de lengte als de hoogte laten veranderen.
In zijn nieuwe ontwerp is de breedte van het grondvlak van een piramide gelijk aan 2 dm en de lengte van dat grondvlak gelijk aan x dm. Voor de hoogte in dm van een piramide neemt hij weer:  h = 9 - ax .
Voor de inhoud van een piramide in dit nieuwe ontwerp geldt dan de formule:    I  = 6x - 2/3ax2
       
3p.

3.

 Toon dit aan door deze formule af te leiden uit de gegevens.
     

  

Als a = 0,5 is de inhoud van zo’n nieuwe piramide maximaal als x = 9. De waarde van x waarvoor de inhoud van zo’n nieuwe piramide maximaal is, is niet steeds gelijk, maar hangt af van a.
Deze waarde van x noemen we xMAX.
       
4p.

4.

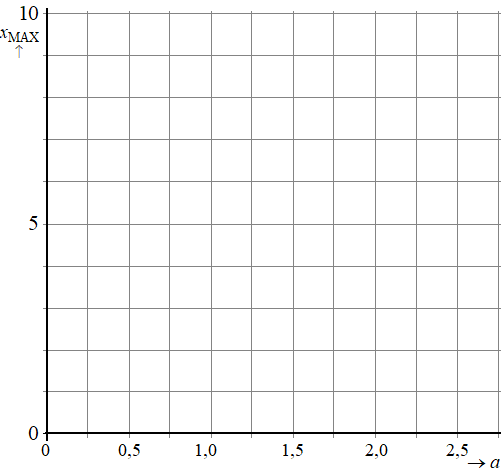
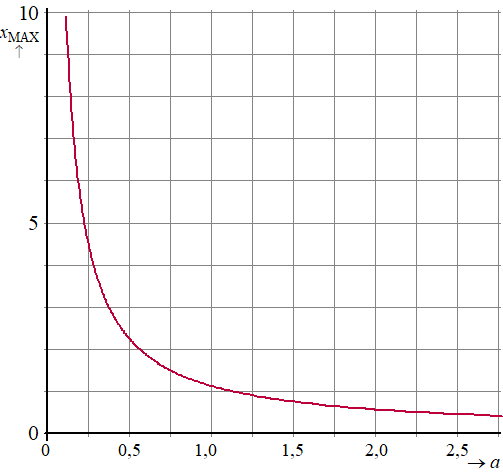
Teken in onderstaand assenstelsel de grafiek van het verband tussen xMAX en a. Licht je werkwijze toe.
       
 

     

   

 

Kosten van betalingsverkeer.
       
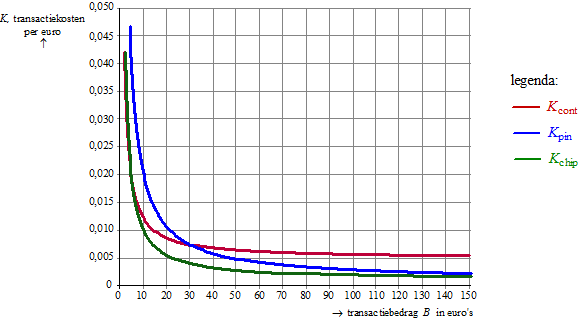
Winkeliers maken kosten bij elke betaling die een klant voor een aankoop doet. Uit een onderzoek van het Hoofdbedrijfschap Detailhandel uit 2002 blijkt dat deze kosten afhangen van de manier waarop de klant zijn aankoop betaalt. Alle bedragen in deze opgave hebben betrekking op het jaar 2002. Om de kosten voor de detailhandel bij contant betalen, pinnen en chippen met elkaar te kunnen vergelijken, is de onderstaande figuur gemaakt. Daarin zie je de kosten voor deze drie betaalmiddelen in grafieken weergegeven. De figuur staat ook vergroot op de uitwerkbijlage. Langs de verticale as staan de transactiekosten per euro K voor elk type betaling. Die transactiekosten K zijn in euro’s. Langs de horizontale as staat het transactiebedrag B in euro’s
       

       
In deze figuur kun je bijvoorbeeld aflezen dat bij een transactiebedrag van € 20 chippen het voordeligst is, namelijk ongeveer € 0,006 per euro. Nu kunnen we de transactiekosten voor een transactie van € 20 chippen berekenen, namelijk (ongeveer) € 0,006 × 20 = € 0,12.
       
4p.

5.

 Bereken met behulp van de figuur het verschil in transactiekosten bij contant betalen en chippen bij een transactiebedrag van € 80.
       
Bij de grafieken in de figuur kunnen we formules opstellen. Voor contant betalen geldt:
       

       
Hierin is Kcont de transactiekosten per euro bij contant betalen in euro’s. Uitgaande van de formule voor Kcont kunnen we een formule opstellen voor de transactiekosten bij contant betalen. Deze kosten geven we aan met TKcont. De formule heeft de vorm TKcont = aB + b
       
4p.

6.

 Laat dit zien en bepaal a en b.
     

  
Bij de grafiek van transacties met pinnen kunnen we de volgende formule opstellen:
       

       
Hierin is Kpin de transactiekosten per euro bij pinnen in euro’s.
Omdat de meeste betalingen contant of per pin uitgevoerd worden, is het snijpunt van Kcont en Kpin belangrijk voor de detailhandel.
       
3p. 7. Bereken met behulp van de formules voor Kcont en Kpin bij welke bedragen de transactiekosten per euro voor het pinnen lager zijn dan voor contant betalen. Rond je antwoord af op centen.
     

  
De formule voor de transactiekosten per euro bij chippen heeft ook de vorm  Kchip = p + q/B  met p en q constanten.

Op basis van de figuur is vast te stellen of p groter of kleiner is dan 0,00488 en ook of q groter of kleiner is dan 0,0744.
       
4p.

8.

 Beredeneer aan de hand van de figuur, zonder p of q te berekenen, of de waarde van p groter of kleiner is dan 0,00488 en beredeneer vervolgens of de waarde van q groter of kleiner is dan 0,0744.
   

 

Station Amersfoort.
       

Op het station van Amersfoort is een trap naar het perron voorzien van een overkapping.
De onderkant van de overkapping (op de foto met een donkere lijn
aangegeven) heeft de vorm van (een deel van) een sinusoïde.

In de figuur hieronder zie je een model van het zijaanzicht van de
overkapping en van de trap naar het perron. Hierin is h de hoogte ten opzichte van het perron en x de horizontale afstand tot het hoogste punt van de overkapping, beide in meters.
       

       

In de figuur is het hoogste punt van de sinusoïde (0; 6,46) en het laagste punt (15; 2,48).

We kunnen voor deze sinusoïde een formule opstellen van de vorm: h(x) = a + b • sin(c(x + 7,5))
Hierbij geldt: a ≈ 4,5; b ≈ 2,0 en c ≈ 0,2.
       

3p.

9.

Bereken met behulp van het hoogste en het laagste punt van de sinusoïde de waarden van de constanten a, b en c in twee decimalen nauwkeurig.
       

In de figuur is de trap weergegeven met lijnstukken: van (0; 4) via (2,7; 4), (6,9; 2), (8,1; 2) en (12,3; 0) naar (15; 0). We houden dus geen rekening met het feit dat de trap gedeeltelijk uit traptreden bestaat.
Door de gemiddelde hoogte van zowel de trap als van de overkapping te bepalen, kunnen we het verschil hiertussen berekenen.
       

3p.

10.

 Bereken dit verschil.
       

In de figuur lijkt het dat de afdalende delen van de trap steiler zijn dan de maximale daling van de overkapping.
       

4p.

11.

Laat met een berekening aan de hand van de formule zien dat dit het geval is.
       

Met behulp van de formule h(x) = 4,5 + 2,0 • sin(0,2(x + 7,5)) en de beschrijving van de trap kan voor iedere waarde van x het hoogteverschil tussen de overkapping en de trap berekend worden.
       

3p.

12.

Onderzoek of er een waarde van x is, waar het hoogteverschil kleiner is dan 2,35 meter.
       
Bevingen in Japan.
       
De laatste jaren waren de zeebevingen in de buurt van Japan regelmatig in het nieuws. De zeebeving van 11 maart 2011 met de daaropvolgende tsunami zorgde voor grote problemen bij de kerncentrale Fukushima I. Om de reactoren te koelen, werd zeewater in de reactoren gepompt. Dit water lekte, radioactief geworden, weer terug in zee. Hierdoor raakte vis besmet met radioactief jodium en moest de visvangst tijdelijk worden stopgezet.

Radioactief jodium verdwijnt volgens een exponentieel proces. De halveringstijd van radioactief jodium is 8 dagen. Op 6 april 2011 gaven metingen aan dat er 4800 keer de maximaal toegestane hoeveelheid radioactief jodium in het zeewater aanwezig was. De maximaal toegestane hoeveelheid radioactief jodium is 5 becquerel/liter. Op het moment dat de maximaal toegestane hoeveelheid werd bereikt, mocht er weer gevist worden. We gaan ervan uit dat er na 6 april 2011 geen nieuw radioactief jodium meer in zee lekte.
       

5p.

 13. Bereken na hoeveel dagen er weer gevist mocht worden.
     

  
De zeebeving van Sendai in 2011 en de aardbeving van 2004 die een enorme tsunami in de Indische Oceaan veroorzaakte, zijn allebei bevingen met een kracht van 9,0 of meer op de schaal van Richter.
De Amerikaan Charles Richter gebruikte seismogrammen om de magnitude (kracht) van een beving te kunnen bepalen. In de figuur zie je een voorbeeld van een seismogram. In dit seismogram zie je de gemeten trillingen van de aarde als uitwijkingen in mm. De grootste uitwijking in het seismogram heet de maximale amplitude.
       
       
Om de magnitude van een beving te bepalen, gebruikt men de formule van Richter. Hieronder staat een vereenvoudigde versie daarvan:
  M = log(A) + 3
In deze formule is M de magnitude en A de maximale amplitude in mm.

Uit de formule blijkt, dat als de maximale amplitude A tien keer zo groot wordt, de magnitude met 1 eenheid toeneemt.
       

3p.

 14. Toon met behulp van de rekenregels voor logaritmen aan dat  log(10A) + 3 altijd 1 groter is dan log(A) + 3.
     

  

De magnitude neemt dus met 1 eenheid toe als de maximale amplitude 10 keer zo groot wordt. Dus de grafiek van M is afnemend stijgend. Dit kun je ook zien aan de afgeleide van M.
       

4p.

15.

Stel een formule op voor  dM/dA en toon met behulp daarvan aan dat M toeneemt en dat deze toename steeds kleiner wordt.
 
Bij een beving komt heel veel energie vrij. Hierbij wordt een andere formule van Richter gebruikt:
   
  M = 0,67 • log(E) - 0,9
 
Hierin is E de vrijkomende energie in kilojoule en M de magnitude op de schaal van Richter.

Door deze formule te combineren met de formule M = log(A) + 3 is het mogelijk een verband op te stellen tussen de vrijkomende energie E en de maximale amplitude A.

Het verband tussen E en A is te schrijven als:  log(A) + 3 = 0,67 • log(E) -  0,9

Dit verband kan vereenvoudigd worden tot de vorm E =10p • log(A)+q
       

4p.

16.

Bereken de waarden van p en q in deze formule. Rond p en q af op twee decimalen.
       
Snoeken.
       

De snoek is een grote zoetwatervis. Het is één van de bekendste roofvissen in Nederland en wordt veel gevangen door sportvissers. Nederlandse sportvissers meten de lengte van hun vangst. In het buitenland zijn de vissers vaak meer geïnteresseerd in het gewicht van een vis. Dat gewicht is lastig te bepalen aan de waterkant. Voor snoeken is er een eenvoudige formule die het verband tussen lengte en gewicht beschrijft:

G = 0,003 • L3,206

Hierbij is G het gewicht in gram en L de lengte in cm.
       

4p.

17.

Herschrijf de formule in de vorm L = a  • Gb met a en b in één decimaal nauwkeurig.
       

Een vuistregel waarmee de lengte van een mannetjessnoek kan worden berekend, is:

L = 87,0 - 87,0 • e-0,188(t + 0,357)

Hierbij is L de lengte in cm op tijdstip t, en t de leeftijd in jaren.
       

3p.

18.

Beredeneer met behulp van deze formule dat de grenswaarde voor de lengte van een mannetjessnoek 87,0 cm is.
       

3p.

19.

Bereken door middel van differentiëren de waarde van de afgeleide van L voor t = 2 en leg uit wat de betekenis van die waarde is met betrekking tot de lengte van de mannetjessnoek.
       

De formule van L is een voorbeeld van de Von Bertalanffy-formule.
De algemene vorm van de Von Bertalanffy-formule is:

L =  Lmax -  Lmax• e -K( t +  c)

Lmax is de maximale lengte en c is een constante. K is een factor, die afhangt van de snelheid waarmee de vis groeit.

Neem in dit model aan dat vrouwtjes- en mannetjessnoeken bij hun geboorte even lang zijn, namelijk 5,6 cm, en dat de factor K gelijk is.
Omdat vrouwtjessnoeken veel ouder kunnen worden dan mannetjessnoeken, kunnen zij ook veel langer worden, tot wel 130 cm. Voor een vrouwtjessnoek geldt dus dat Lmax = 130.
       

4p.

20.

Stel de Von Bertalanffy-formule op voor de lengte van een vrouwtjessnoek.
       
Number rumba.
         

Het spel Number Rumba kan gespeeld worden met één of twee spelers.
Iedere speler heeft een standaard voor zich met vier staven. Verder heeft een speler 9 verschillende blokjes: 3 blauwe, 3 rode en 3 gele, waarbij de blokjes van elke kleur genummerd zijn van 1 tot en met 3.

Het doel van het spel is om de opstelling van de blokjes op de standaard vanuit een beginopstelling zo snel mogelijk te veranderen in de opstelling die op een opdrachtkaart staat. Hierbij wordt er steeds één blokje verplaatst en mogen niet meer dan drie blokjes tegelijk op een staaf staan.

Foto’s 1 en 2 laten twee mogelijke opstellingen tijdens het spel zien.
         

         

Tijdens het spel kan iedere mogelijke opstelling met de negen blokjes op de vier staven ontstaan.
         

7p.

21.

Onderzoek hoeveel opstellingen er in dit spel in totaal mogelijk zijn met de negen blokjes op de vier staven.
         

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. a = 1  geeft  h = 9 - x
x = 2,5 geeft dan h = 9 - 2,5 = 6,5
I = 1/3 • 2,5 • 2,5 • 6,5 = 13,54 dm3
   
2. I = 1/3x2(9 - x) = 3x2 - 1/3x3
I ' =  6x - x2
I ' = 0   geeft dan  6x - x2 = 0  ⇒  x(6 - x) = 0   ⇒  x = 0  of  x = 6
maximale inhoud bij x = 6 
   
3. grondvlak is nu 2 bij x  dus oppervlakte is 2x
h = 9 - ax
I = 1/3 • 2x • (9 - ax) = 2/3x(9 - ax) = 2/3x • 9 - 2/3x • ax  = 6x - 2/3ax2
   
4.. I = 6x - 2/3ax2
I ' = 6 - 4/3ax = 0
6 = 4/3ax
18 = 4ax
x = 18/4a

Dat geeft deze grafiek:
   
 

   
5. Aflezen:
B = 80  geeft  Kchip = 0,0025  dus de kosten zijn dan  0,0025 • 80 = 0,20
B = 80  geeft  Kcont = 0,006  dus de kosten zijn dan  0,006 • 80 = 0,48
Dat scheelt  0,48 = 0,20 = 0,28 euro
   
6. TK = K • B
TK = (0,00488 + 0,0744/B) • B
TK = 0,00488 • B  +  0,0744/B • B
TK = 0,00488B + 0,0744
dus a = 0,00488  en  b = 0,0744
   
7. snijpunt berekenen:
0,00488 + 0,0744/B = 0,00093 + 0,193/B
0,00488 - 0,00093 = 0,193/B - 0,0744/B
0,00395 = 0,1186/B
B = 0,1186/0,00395 = 30,0253 = 30,03
De transactiekosten voor pinnen zijn lager vanaf B = 30,03

(het kan uiteraard ook met de GR en dan intersect)
   
8. Om de grafiek van  K = p + q/B  te krijgen is de grafiek van  K = 1/B   vermenigvuldigd tov de B-as met factor q (en daardoor q keer zo steil geworden) en vervolgens p omhoog geschoven

p geeft dus de horizontale asymptoot.
omdat de asymptoot van Kchip lager ligt dan die van Kcont is p < 0,00488

q geeft aan hoe snel de grafiek daalt.
omdat de grafiek van Kchip sneller daalt dan de grafiek van Kcont is q > 0,0744
   
9. (0; 6,46) en het laagste punt (15; 2,48).

Het gemiddelde van de y-coördinaten is (6,46 + 2,48)/2 = 4,47 = a en dat is de evenwichtslijn.

De afstand van een top tot de evenwichtslijn is 6,46 - 4,47 = 1,99 = b en dat is de amplitude.

de afstand tussen de toppen is 15 - 0 = 15 en dat is een halve periode, dus de periode is 30
dan is 2π/30 = 0,21 = c
   
10. De gemiddelde hoogte van de overkapping is de evenwichtslijn en die is 4,5 meter
De gemiddelde hoogte van de trap is 2meter want hij is symmetrisch en het midden zit op hoogte 2 meter.
Het hoogteverschil is dus 2,5 meter.
   
11. De daling van de trap is  (2 - 4)/(6,9 - 2,7) = -2/4,2 = -0,476

De overkapping heeft maximale helling in het midden bij x = 7,5
GR op RAD!
Y1 =    4,5 + 2,0 • sin(0,2(X + 7,5))
calc - dy/dx  en dan X = 7,5  geeft helling  -0,396

De delen van de trap zijn dus inderdaad steiler dan de maximale daling van de overkapping.
   
12. Bij x = 2,7 heeft de trap hoogte 4
h(2,7) = 6,284
Het verschil is daar 2,284 en dat is kleiner dan 2,35
Er is dus een punt waar het hoogteverschil minder dan 2,35 meter is.
   
13. Als de halveringstijd gelijk is aan 8 dagen dan is  g8 = 0,5
g = 0,5(1/8) = 0,917
Eindwaarde is 5,  beginwaarde is  4800 • 5 = 24000
y = B • gt  invullen:   5 = 24000 • 0,917t
Het mag nu met de GR (intersect) maar het kan natuurlijk ook algebraïsch:
5/24000 = 0,0002083 = 0,917t
t = log(0,0002083)/log(0,917) = 97,8 dagen.
   
14. log(10A) = log(10) + log(A)  = 1 + log(A)   want log(10) = 10log(10) = 1
Dat is dus één meer dan log(A)
   
15. M = log(A) + 3
dM/dA = M' =  1/(Aln10)  = 1/2,3A
Omdat A positief is, is M' ook positief dus de grafiek van M stijgt.

Als A groter wordt, dan wordt de noemer van M' groter, dus wordt M' zelf kleiner.
Het stijgen neemt dus af.
   
16. log(A) + 3 = 0,67 • log(E) -  0,9
log(A) + 3,9 = 0,67log(E)
1/0,67 • (log(A) + 3,9)) = log(E)
1,4925(log(A) + 3,9) = log(E)
1,4925log(A) + 5,8209 = log(E)
E = 101,4925log(A) + 5,8209

Dus p = 1,49  en  q = 5,82
   
17. G = 0,003 • L3,206
1/0,003 • G = L3,206 
333,33G = L3,206
L = (333,33G)1/3,206
L = (333,33G)0,3119 
L = 333,330,l3119 • G0,3119
L = 6,1224 • G0,3119 
L = 6,1 • G0,3 
   
18. L = 87,0 - 87,0 • e-0,188(t + 0,357)  
Als t heel groot wordt, dan wordt de exponent van e een heel groot negatief getal
e(.....)  wordt dan bijna nul.
het tweede deel van de formule gaat naar nul, dus de waarde van L nadert dan naar 87,0.
   
19. L ' = -87,0 • e -0,188(t + 0,357)   • -0,188
L '(2) = -87,0 • e-0,188(2 + 0,357) • -0,188 = 10,50

Bij een leeftijd van 2 jaar groeit de lengte van een mannetjessnoek met ongeveer 10,5 cm per jaar.
   
20. L = 130 -  130 • e -0,188( t +  c) 
t = 0  met L = 5,6 geven:   5,6 = 130 - 130 • e-0,188c
-124,4 = -130 • e-0,188c
0,9569 = e-0,188c
-0,188c = ln(0,9569) = -0,0440
c = 0,2342
De formule wordt  L = 130 - 130 • e-0,188(t + 0,234)
   
21. Er zijn drie mogelijkheden voor de aantallen blokjes op de pinnen:

3330 en dat kan op 4 manieren (kies de plaats van de 0)

3321 en dat kan op  (4 nCr 2) • 2 = 6 • 2 = 12 manieren
(de 33 kun je op 4nCr2 = 6 manieren kiezen, en daarna zijn er nog 2 manieren om de 2 en de 1 te kiezen)

3222 en dat kan op 4 manieren  (kies de plaats van de  3)

Samen geeft dat 20 manieren

Omdat alle blokjes verschillend zijn zijn er bij elke manier 9 • 8 • .... • 1 = 9! = 362880 manieren om de blokjes te verdelen.
In totaal zijn er dus 20 • 362880 = 7257600 manieren.