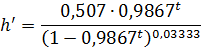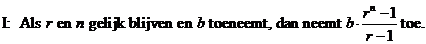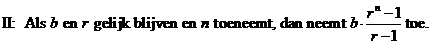VWO WA, 2010 - I
 

 

Marathonloopster
     
De Olympische hardloopwedstrijd met de grootste lengte is de marathon: ruim 42 kilometer, om precies te zijn 42195 meter. De marathon wordt zowel door mannen als door vrouwen gelopen. In deze opgave concentreren we ons op de
marathonloopsters.
De prestatie van een loopster geeft men in krantenberichten meestal weer door de tijd waarin de marathon is afgelegd, maar een even duidelijke maat is de gemiddelde snelheid over het gehele parcours. Dit noemen we kortweg de snelheid. Deze snelheid drukken we uit in m/s (meters per seconde).

Een marathonloopster legt de marathon af in 2 uur, 43 minuten en 32 seconden.
       
3p. 1. Bereken haar snelheid in m/s.
     

 
Elmer Sterken van de Rijksuniversiteit Groningen heeft onderzoek gedaan naar het verband tussen de snelheid van Amerikaanse marathonloopsters en hun leeftijden. De figuur hieronder is afkomstig uit het rapport dat hij daarover geschreven heeft. In onderstaande figuur is voor iedere leeftijd weergegeven de hoogste snelheid ooit gelopen door een Amerikaanse (zie de ‘zigzaglijn’). De geregistreerde leeftijden lopen van 6 tot en met 90 jaar1).
       

   
  noot 1:  Deze figuur is ontstaan door allerlei gegevens van verschillende loopafstanden (op verantwoorde manier) om te zetten naar de marathonlengte. Hierdoor zijn in deze figuur ook voor een marathon onwaarschijnlijk jonge leeftijden vermeld.
       
De ‘zigzaglijn’ is in deze figuur benaderd door de grafiek met de formule:

v = 2,836 • x0,665 −1,390• x0,818

Hierin is v de hoogste snelheid in m/s van marathonloopsters met een leeftijd van x jaar. In de figuur hieronder is de grafiek van v weergegeven.
       

       
In het vervolg van deze opgave beschouwen we deze laatste grafiek en de formule voor v als een wiskundig model van de werkelijkheid.

Petra loopt vaker een marathon en hoopt binnenkort de marathon binnen 3 uur te volbrengen. Petra is 52 jaar.
       
3p. 2. Kan een 52-jarige marathonloopster volgens dit model de marathon binnen 3 uur lopen? Licht je antwoord toe.
       
De grafiek van v heeft een maximum. Volgens het model is er dus blijkbaar een leeftijd waarop marathonloopsters (gemiddeld) het beste presteren.
       
5p. 3. Stel de afgeleide van v op en bereken hiermee deze leeftijd.
     

 
Stoppen met roken.
       
Veel mensen beginnen op jonge leeftijd met roken en proberen daar op latere leeftijd weer mee op te houden. Dat lukt niet altijd.
Het Centraal Bureau voor de Statistiek (CBS) publiceert regelmatig cijfers waarmee het rookgedrag van Nederlanders kan worden bestudeerd. In de volgende tabel vind je enkele getallen.
       
rokers en aantallen sigaretten
jaar 2001 2005
aantal Nederlanders, in miljoenen 16,0 16,3
percentage rokers 33,3% 29,5%
gemiddeld aantal sigaretten per roker per jaar 4526 4271
       
4p. 4. Bereken met hoeveel procent het totale aantal gerookte sigaretten in 2005 is afgenomen ten opzichte van 2001.
     

 
Er zijn veel hulpmiddelen om minder te gaan roken of er zelfs helemaal mee te stoppen. Eén daarvan is het gebruik van tabletten van het merk Fumostop.
Om na te gaan of Fumostop een middel is dat inderdaad helpt, wordt het volgende onderzoek uitgevoerd.
Uit alle zware rokers wordt aselect een groep van 18 proefpersonen gekozen. Elke proefpersoon krijgt 10 tabletten die uiterlijk niet van elkaar verschillen. De tabletten zijn verpakt in doordrukstrips met bij elk tablet een nummer. Zie de figuur.
       
       
Elke proefpersoon moet 10 dagen lang iedere dag bij het opstaan één willekeurig gekozen tablet innemen, het nummer van dat tablet noteren en bijhouden hoeveel sigaretten hij die dag rookt.
Wat de proefpersonen niet weten maar de onderzoekers wel, is dat 5 van de tabletten inderdaad van het merk Fumostop zijn. De andere 5 tabletten bevatten geen enkele werkzame stof. We geven de ‘echte’ tabletten aan met F en de andere tabletten met NF. Aan de genoteerde tabletnummers kunnen de onderzoekers zien wanneer de F- en de NF-tabletten ingenomen zijn.
Nico is één van de 18 proefpersonen. De mogelijkheid bestaat dat hij om de dag een F-tablet inneemt, waarmee bedoeld wordt dat hij de ene dag een F-tablet en de andere dag een NF-tablet inneemt.
       
4p. 5. Bereken de kans dat hij om de dag een F-tablet inneemt.
     

 
De proefpersonen kiezen hun tabletten iedere dag dus volledig aselect. Het kan dus gebeuren dat een proefpersoon de eerste dag een van de tabletten met nummer 1 of nummer 2 kiest.
       
4p. 6. Bereken hoe groot de kans is dat 6 of meer proefpersonen op de eerste dag van het onderzoek een van de tabletten met nummer 1 of 2 kiezen.
     

 
De onderzoekers vermoeden dat het gebruik van F-tabletten leidt tot het roken van minder sigaretten. Om dat na te gaan, wordt van elke proefpersoon bijgehouden hoeveel sigaretten hij in totaal heeft gerookt op de vijf dagen met een F-tablet en op de vijf dagen met een NF-tablet. Het resultaat vind je in de volgende tabel.
       
proefpersoon 1 2 3 4 5 6 7 8 9
bij gebruik van F-tabletten 106 90 109 72 103 118 124 103 89
bij gebruik van NF-tabletten 112 108 132 92 96 120 145 129 101
       
proefpersoon 10 11 12 13 14 15 16 17 18
bij gebruik van F-tabletten 87 92 145 101 100 97 112 104 101
bij gebruik van NF-tabletten 104 127 138 124 121 139 100 93 118
       
6p. 7. Onderzoek met behulp van een tekentoets of er voldoende aanleiding is om het vermoeden van de onderzoekers te bevestigen. Neem hierbij als significantieniveau 5%.
     

 
Van de mensen die in 2006 rookten, rookte 24,5% per dag 20 sigaretten of meer. Rokers rookten toen gemiddeld 11,4 sigaretten per dag. Tine wil onderzoeken of het aantal sigaretten per dag normaal verdeeld zou kunnen zijn.
Ze bedenkt de volgende aanpak: “Als er sprake is van een normale verdeling, dan kan ik de bijbehorende standaardafwijking berekenen. Daarna kan ik nagaan of die waarde – in combinatie met dat gemiddelde 11,4 – tot een conclusie leidt.”
       
4p. 8. Bereken die standaardafwijking en toon daarmee aan dat het aantal sigaretten dat een roker per dag in 2006 rookte, niet normaal verdeeld kan zijn.
     

 
Boomgroei.
       
Naar de groei van bomen is veel onderzoek gedaan. Dat heeft geleid tot een goed inzicht in het verband tussen de hoogte van een boom en de leeftijd van die boom. In de bosbouw wordt voor veel bomen de te verwachten hoogte berekend met de formule van Chapman-Richards:

h = a(1 - bt)c
       
Hierin is h de hoogte van een boom in meters en t de leeftijd in jaren. De waarden van de getallen a, b en c hangen af van de soort boom. De getallen a, b en c zijn positief. In de volgende tabel zijn deze waarden voor enkele boomsoorten weergegeven.
       
boom a b c
Japanse lariks 23,743 0,9603 1,22770
zomereik 39,143 0,9867 0,96667
Amerikaanse eik 29,026 0,9790 0,80820
berk 43,281 0,9876 0,95040
grove den 24,426 0,9656 1,59980
       
Het verband tussen de hoogte en de leeftijd van de zomereik wordt dus gegeven door de formule:
       

h = 39,143(1 - 0,9867t)0,96667
       
De zomereik wordt op den duur veel groter dan de Amerikaanse eik, maar in de eerste levensjaren groeit de Amerikaanse eik veel sneller.
       
5p. 9. Toon door berekening aan dat volgens de formule van Chapman-Richards de Amerikaanse eik in het vierde levensjaar ruim 20 cm méér groeit dan de zomereik.
     

 
Elke boom groeit, maar die groei gaat steeds langzamer. We kunnen dit nagaan met behulp van de afgeleide van h. Dat gaan we hier doen voor de zomereik. Voor de snelheid waarmee deze boomsoort groeit, kijken we naar de formule voor de afgeleide:
       

       
Aan de vorm van deze afgeleide kun je door redeneren, dus zonder berekeningen uit te voeren, zien dat de zomereik steeds groeit en dat die groei steeds langzamer gaat.
       
6p. 10. Laat zien (door een redenering) hoe uit de formule van de afgeleide volgt dat de zomereik steeds groeit en dat deze groei steeds langzamer gaat.
     

 
Voor de formule voor de zomereik hebben we gebruik gemaakt van de waarden van a, b en c uit de tabel. Maar niet alle zomereiken hebben de waarde 39,143 voor a.
Factoren zoals klimaat en bodemgesteldheid beïnvloeden de waarde van a.
Chapman en Richards gaan er in hun model van uit dat de waarden van b en c uitsluitend afhangen van de boomsoort.
Vaak weet men niet van tevoren welke waarde van a een boom heeft. Om de waarde van a voor een boom te bepalen, laat men de boom eerst een aantal jaren groeien.
Daarna meet men de boom op en berekent men welke waarde van a past bij de groei van die boom. Men gaat ervan uit dat die waarde van a daarna niet meer verandert.

Een zomereik bereikt op de leeftijd van 10 jaar een hoogte van 6,18 meter.
       
3p. 11. Bereken de waarde van a die hierbij hoort.
     

 
Afhankelijk van de waarde van a krijgen we verschillende groeiformules. In de volgende figuur zie je de grafieken van enkele groeiformules van de grove den. De waarde van a staat er steeds bij vermeld.
       

       
Het ziet ernaar uit dat je aan de waarde van a kunt zien hoe groot de verschillende grove dennen uiteindelijk worden.
       
4p. 12. Onderzoek aan de hand van de formule of dit inderdaad het geval is voor de grafiek die hoort bij a = 30,1.
     

 
Als je naar de figuur hierboven kijkt, kun je je afvragen of deze grafieken door de oorsprong (0, 0) gaan als we ze verder naar links zouden doortekenen. Dit is inderdaad het geval.
Sterker nog: dit is het geval voor alle grafieken die horen bij de algemene formule  h(t) = a(1 − bt)c  van Chapman-Richards.
       
4p. 13. Beredeneer, dus zonder getallenvoorbeelden te gebruiken, dat alle grafieken die horen bij de formule van Chapman-Richards door de oorsprong gaan.
     

 
Inkomen.
       
Het CBS (Centraal Bureau voor de Statistiek) besteedt elk jaar aandacht aan de verdeling van de inkomens van huishoudens in Nederland. In de volgende tabel is voor het jaar 2004 weergegeven hoeveel huishoudens in een bepaalde inkomensklasse zaten.
       
besteedbaar inkomen in euro's aantal huishoudens in duizendtallen
0 - 10000 490
10000 - 20000 2057
20000 - 30000 1777
30000 - 40000 1309
40000 - 50000 687
50000 - 70000 460
meer dan 70000 197
       
Met behulp van lineair interpoleren kun je een schatting maken van het percentage huishoudens met een besteedbaar inkomen van ten hoogste 27000 euro.
       
5p. 14. Schat dat percentage huishoudens met behulp van lineair interpoleren.
     

 
De verdeling van de inkomens is geen normale verdeling, zelfs niet bij benadering.
Dat kun je bijvoorbeeld zien door het histogram (Een histogram wordt ook wel staafdiagram genoemd) te tekenen voor de inkomensklassen 0 – 10000 tot en met 40000 – 50000.
       
4p. 15. Teken dit histogram en leg met behulp daarvan uit dat deze frequentieverdeling niet kan worden benaderd met een normale verdeling.
     

 
Toch is er wel een manier om de tabel in verband te brengen met een normale verdeling. Dat gaat als volgt:
We geven de inkomens aan met X en berekenen van alle inkomens de logaritme. Die noemen we L, dus L = log(X ) . We krijgen dan voor L een klassenindeling met andere grenzen. Omdat log(0) niet bestaat, nemen we bij de eerste klasse als linkergrens log(1) .
Deze klassenindeling levert wel (bij benadering) een normale verdeling op.
       
6p. 16. Maak de frequentieverdeling die bij L hoort en toon met behulp van normaal waarschijnlijkheidspapier aan dat deze frequentieverdeling bij benadering normaal verdeeld is  (hier kun je een velletje vinden).
     

 

 

Verzekering.
       
Verzekeringsmaatschappijen maken op verschillende manieren reclame voor allerlei verzekeringen. Een voorbeeld daarvan vind je in de figuur hieronder. Daar zie je een deel van een reclamefolder die in 2004 huis aan huis werd verspreid.
In de folder legt de verzekeraar uit dat de kosten voor een uitvaart sneller stijgen dan de kosten voor het levensonderhoud. Ook wordt de ontwikkeling van beide kostensoorten met een grafiek in beeld gebracht.
       

       
Uitgaande van een jaarlijkse kostenstijging met 4,5% berekende men de kosten in 2044. De uitvaartkosten stijgen van € 4700 in 2004 tot ongeveer € 27000 in 2044.

Het bedrag in 2044 is afgerond op duizendtallen.
       
3p. 17 Bereken dit bedrag in euro’s nauwkeurig.
     

 
Met “anderhalf keer harder” bedoelt de schrijver van de folder dat de jaarlijkse procentuele stijging van de kosten voor een uitvaart 1,5 keer zo groot is als die van de kosten voor het levensonderhoud. Daardoor zullen de kosten voor het levensonderhoud in de periode 2004─2044 stijgen met een percentage dat aanzienlijk kleiner is dan 474% (het stijgingspercentage van de uitvaartkosten).
Dit is in de folder ook grafisch weergegeven.
       
3p. 18. Bereken met hoeveel procent de kosten voor het levensonderhoud volgens de folder zullen toenemen in de periode 2004─2044.
     

 
Op de achterzijde van de folder doet de verzekeraar een aanbod om de kosten van een uitvaart te verzekeren. Wie aan deze verzekering deelneemt, betaalt maandelijks een premie. De hoogte daarvan hangt af van de leeftijd van de verzekeringnemer op het moment dat de verzekering wordt afgesloten. De verzekeraar bepaalt die hoogte onder andere op grond van de gemiddelde leeftijd van overlijden in Nederland. Voor iemand die volgens deze inschatting van de verzekeraar gemiddeld nog 40 jaar lang premie zal betalen, bedraagt de premie € 4,79 per maand.
De verzekeraar gaat deze premiegelden beleggen. De jaarlijkse procentuele stijging op zijn beleggingen wordt het jaarlijkse rendement van de beleggingen genoemd.
De premies en de winst van de beleggingen kunnen samen uitgroeien tot een bedrag waarmee de uitvaart kan worden betaald.
De verzekeraar maakt bij zijn berekeningen gebruik van de volgende formule:
       

       
In deze formule is b de maandelijkse premie, r de groeifactor van de beleggingen per maand en n het aantal maanden dat er (naar verwachting) premie moet worden betaald.
Uit de folder blijkt dat de verzekeraar ervan uitgaat dat bij een maandelijkse premie van € 4,79 de opbrengst na 40 jaar minstens € 27 000 zal zijn.
       
6p. 19. Onderzoek hoeveel het jaarlijkse rendement op zijn beleggingen dan moet zijn.
     

 
Als de maandelijkse premie verhoogd wordt of als er gedurende meer maanden betaald wordt, zal de opbrengst natuurlijk toenemen.
We gaan ervan uit dat altijd geldt: r >1.
De juistheid van de beweringen I en II kun je beredeneren door uitsluitend gebruik te maken van de formule

dus zonder te rekenen of te differentiëren.
       
4p. 20. Toon door redeneren met behulp van de formule de juistheid van de beweringen I en II aan.
     

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
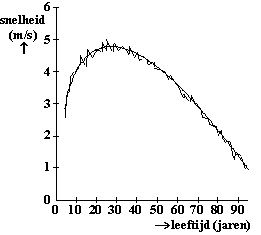
1. 2 uur en 43 minuten en 32 seconden is  2 • 3600  + 43 • 60 + 32 = 9812 seconden
De snelheid is dan  42195/9812 = 4,3 m/s
   
2. x = 52  geeft  v = 2,836 • 520,665 - 1,390 • 520,818  = 4,0376
dan is de tijd  42195/4,0376 = 10451 seconden en dat is minder dan 3 uur (3 uur is 10800 seconden)
Dus het kan volgens dit model WEL.
(opm.: volgens het model kan het eigenlijk altijd wel, want het model zegt iets over gemiddelden en niets over individuen)
   
3. de afgeleide:  v' =  0,665 • 2,836 • x-0,335 - 0,818 • 1,390 • x-0,182  =
Dat moet nul zijn voor het minimum.
Voer in de GR in  Y1 = 0,665 • 2,836 • x-0,335 - 0,818 • 1,390 • x-0,182
Gebruik dan calc - minimum  en dat levert  x ≈ 27 jaar 
   
4. in 2001 waren er  0,333 • 16,0 = 5,328 miljoen rokers die elk 4526 sigaretten rookten.
Dat zijn in totaal 24114,528 miljoen sigaretten

in 2005 waren er  0,295 • 16,3 = 4,8085 miljoen rokers in Nederland die elk 4271 sigaretten rookten
Dat zijn in totaal  20537,1035 miljoen sigaretten.

de afname is  24114,528 - 20537,1035 = 3577,4245 miljoen sigaretten
Dat is  3577,4245/24114,528 • 100% = 14,8%
   
5. Er zijn twee mogelijkheden: 
F, NF, F, NF, F, NF, F, NF, F, NF  en   NF, F, NF, F, NF, F, NF, F, NF, F
De kans op beiden is gelijk, en die is  5/10 • 4/9 • 4/8 • 4/7 • 3/6 • 3/5 • 2/4 • 2/3 • 1/2 • 1 = 1/252
De totale kans is daarom  2 • 1/252 = 1/126 ≈ 0,008

(of: er zijn  10 nCr 5 = 252 mogelijkheden, waarvan 2 gunstig, dus de kans is  2/252)
   
6. Voor één persoon is die kans  0,2.
Het aantal proefpersonen dat de eerste dag tablet 1 of 2 kiest is binomiaal verdeeld.
Het aantal experimenten is n = 18.
De kans op succes (1 of 2 kiezen) per keer is 0,2
Het gaat om 6 of meer successen, dus  P(X ≥ 6) = 1 - P(X ≤ 5) = 1 - binomcdf(18, 0.2, 5) = 0,133
   
7. Stel p de kans dat het aantal sigaretten bij gebruik van NF-tabletten groter is dan bij gebruik van F-tabletten.
H0:  er is geen verschil,  p = 0,5
H1:  bij F-tabletten minder,   p > 0,5
De tabel geeft in 14 van de 18 gevallen en lager aantal
De overschrijdingskans is P(X ³ 14)  met de binomiale verdeling  n = 18 en p = 0,5
P(X ≥ 14)  = 1 - P(X ≤ 13) = 1 - binomcdf(18, 0.5, 13) = 0,01544
Dat is minder dan 5% dus H0 moet worden verworpen.
Er is dus WEL voldoende aanleiding om het vermoeden van de onderzoekers te bevestigen.
   
8. 20 of meer betekent in de klokvorm de oppervlakte vanaf 19,5.  (continuïteitscorrectie)
normalcdf(19,5, 10000..., 11.4, X) = 0,245
voer in de GR in:  Y1 = normalcdf(19,5, 100000, 11.4, X)  en  Y2 = 0,245
intersect geeft  X = σ = 11,7
Als het gemiddelde 11,4 is, dan kan de standaardafwijking nooit 11,7 zijn, want dat zou betekenen dat een aantal rokers minder dan nul sigaretten per dag zou roken!
Daarom zal het aantal sigaretten niet normaal verdeeld zijn.
   
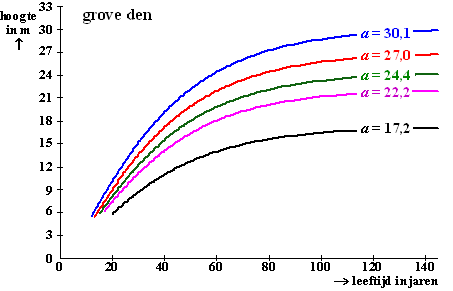
9. De groei in het vierde jaar is gelijk aan  h(4) - h(3)

Amerikaanse eik:  h = 29,026 • (1 - 0,9790t)0,80820
h(4) = 305,5  en  h(3) = 382,2  dus in het vierde jaar is de Amerikaanse eik  77 cm gegroeid

zomereik:  h = 39,143(1 - 0,9867t)0,96667
h(4) = 225,2  en  h(3) = 171,7 dus in het vierde jaar is de zomereik 54 cm gegroeid.

het verschil is 77 - 54 en dat is inderdaad ruim 20 cm
   
10. Als de zomereik steeds groeit, dan moet de afgeleide altijd positief zijn.
Dat kun je als volgt zien:
   0,9867t  is altijd kleiner dan 1, dus  1 - 0,9867t is altijd groter dan nul.
   dan is dat getal tot de macht 0,03333 ook altijd groter dan nul, dus de noemer van h' is groter dan nul.
   0,9867t is altijd groter dan nul, dus is de teller van h' ook altijd groter dan nul.
   Omdat zowel de teller als de noemer groter dan nul zijn is h' altijd groter dan nul.

Als de zomereik steeds langzamer groeit, dan moet h' steeds kleiner worden.
Dat kun je als volgt zien:
   Als t groter wordt, dan wordt  0,9867t steeds kleiner  (want 0,9867 < 1) dus wordt de teller kleiner
   Als t groter wordt, dan wordt 0,9867t steeds kleiner, dus wordt  1 - 0,9867t steeds groter
   maar dan wordt  dat getal tot de macht 0,03333 ook steeds groter.
   Dus de teller wordt kleiner en de noemer wordt groter, dat betekent dat de breuk zelf kleiner wordt.
   
11. zomereik:  h(t) = a • (1 - 0,9867t )0,96667  
vul in  h = 6,18 en t = 10:   6,18 = a • (1 - 0,986710 )0,96667
⇒  6,18 = a • (0,12532)0,96667   ⇒  6,18 = a • 0,1343  Þ  a = 46,02
   
12. h(t) = 30,1 • (1 - 0,9656t)1,59980
Als t heel erg groot wordt, dan wordt 0,9656t ongeveer gelijk aan nul.
Dan is  h(t)  ≈ 30,1 • (1 - 0)1,59980 = 30,1 • 11,59980 = 30,1.
Het klopt dus.
   
13. h = a(1 - bt)c
Neem t = 0 dan is  h(0) = a(1 - b0)c = a(1 - 1)c  want een getal tot de macht nul is altijd 1.
dus  h(0) = a • 0c = a • 0 = 0  dus de grafieken gaan inderdaad allemaal door de oorsprong.
   
14. Het totaal aantal huishoudens is 6977 (duizend); tel de tweede kolom op.

het zijn in ieder geval alle huishoudens uit de eerste twee klassen en dat zijn er al 490 + 2057 = 2547
de klasse 20000 - 30000 heeft klassebreedte 10000
20000 - 27000 heeft breedte 7000 dus dat is 7/10 deel daarvan
Dan zal het aantal huishoudens ook 7/10 deel zijn:  7/10 • 1777 = 1244  (afgerond)
In totaal zijn er dan 2547 + 1244 = 3791 duizend huishoudens onder de 27000 euro.
Dat is  3791/6977 • 100% = 54,3%
   
15.

   
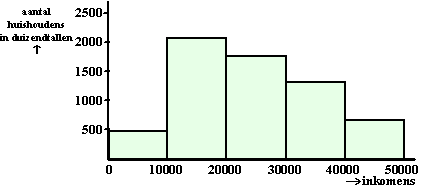  Een normale verdeling is symmetrisch dit histogram duidelijk niet. Daarom zal het geen normale verdeling zijn.
   
16. Dat geeft de volgende tabel:
 
inkomensklasse rechtergrens log(L) frequentie cumulatieve frequentie  cum. freq.
in procenten
0 - 10000 10000 4,00 490 490 7,0
10000 - 20000 20000 4,30 2057 2547 36,5
20000 - 30000 30000 4,48 1777 4324 62,0
30000 - 40000 40000 4,60 1309 5633 80,7
40000 - 50000 50000 4,70 687 6320 90,6
50000 - 70000 70000 4,85 460 6780 97,2
   
  Op normaalpapier ziet dat er zó uit:
 

   
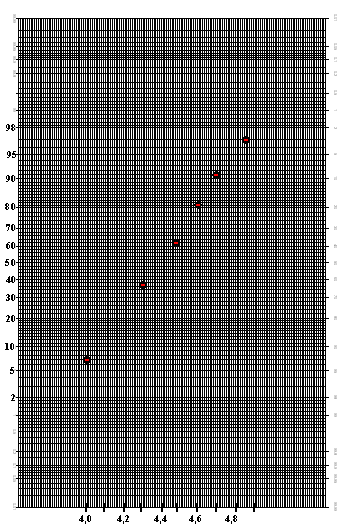  Omdat de waarden redelijk goed op een rechte lijn liggen is er sprake van een normale verdeling.
   
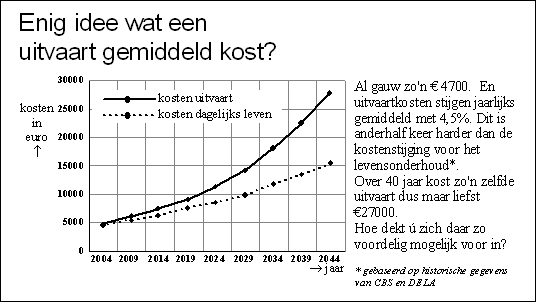
17. 4,5% groei betekent een groeifactor van 1,045
2044 is 40 jaar na 2004.
Dan zijn de kosten 4700 • 1,04540 = 27337 euro
   
18. aflezen: de kosten voor het levensonderhoud zullen stijgen tot ongeveer 15500 euro
Dat is een factor  15500/4700 = 3,298
dat is een toename van 229,8%  ofwel ongeveer 230%
   
19. 40 jaar is 40 • 12 = 480 maanden, dus n = 480.
 
  Voer in de GR in:   Y1 = 27000 en  Y2 = 4,79*(X^480 - 1)/(X-1)
Intersect levert  X = r = 1,008
De groeifactor per jaar is dan  1,00812 = 1,10
Dat is een rendement van 10%
   
20. Als r en n gelijk blijven, dan blijft de hele breuk uit de formule gelijk, dus als b dan toeneemt zal de opbrengst ook toenemen. (die breuk is positief, want r > 1)

Als n toeneemt, dan neemt rn - 1 ook toe  (want r > 1), dus zal de breuk ook toenemen, dus de opbrengst ook (want b blijft gelijk)