VWO WA, 2001 - II

 

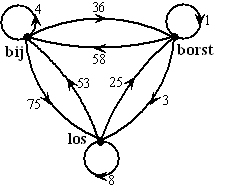
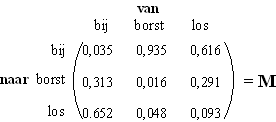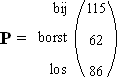OPGAVE 1.  Vakkenkeuze.
       
In het voorjaar van 1994 zijn bij een onderzoek naar vakkenkeuze 344 jongens en 493 meisjes ondervraagd die toen eindexamen deden.
Nederlands was voor iedereen verplicht. Havo-leerlingen moesten naast Nederlands nog tenminste 5 andere vakken kiezen. In de tabel hieronder is te zien door hoeveel procent van de ondervraagden de andere vakken zijn gekozen.
       
vak jongens (in %) meisjes (in %)
Duits 31,1 46,7
Engels 98,8 97,6
Frans 10,2 38,5
Aardrijkskunde 19,2 28,2
Geschiedenis 25,3 30,2
Economie 60,2 47,9
Handelswetenschappen 43,0 29,8
Wiskunde A 43,3 62,3
Wiskunde B 54,7 22,3
Biologie 23,5 45,2
Natuurkunde 57,6 17,0
Scheikunde 42,2 24,5
Tekenen 7,0 15,2
Maatschappijleer 2,9 4,5
Muziek 0,9 3,4
Handenarbeid 2,3 4,9
Textiele werkvormen 0,0 0,4
Spaans 0,0 0,6
       
2p. 1. Toon aan dat van de ondervraagde leerlingen meer meisjes dan jongens economie deden.
       
De meeste leerlingen hadden naast Nederlands 5 vakken gekozen. Sommige leerlingen hadden naast Nederlands 6 vakken gekozen. Geen van de leerlingen had naast Nederlands meer dan 6 vakken gekozen.
       
3p. 2. Bereken hoeveel procent van de ondervraagde meisjes een extra vak deed.
       
Bij het onderzoek werd ook gevraagd of je, als je opnieuw zou mogen kiezen, weer precies hetzelfde vakkenpakket zou hebben gekozen. De onderzoekers vermoedden dat tenminste de helft van de kandidaten ontevreden was over hun huidige pakket.
Een onderwijsdeskundige was het daar niet mee eens. Kort voor het onderzoek beweerde hij dat minder dan de helft van alle HAVO-eindexamenkandidaten achteraf liever een ander pakket gekozen zou hebben.

Neem aan dat de groep van 837 ondervraagde leerlingen een aselecte steekproef vormt uit alle HAVO- eindexamenkandidaten. Van deze groep zouden 359 leerlingen een ander pakket gekozen hebben, zo bleek uit het onderzoek.
       
7p. 3. Onderzoek of bij een significantieniveau van 1% het onderzoeksresultaat voldoende aanleiding geeft om de onderwijsdeskundige gelijk te geven.
       
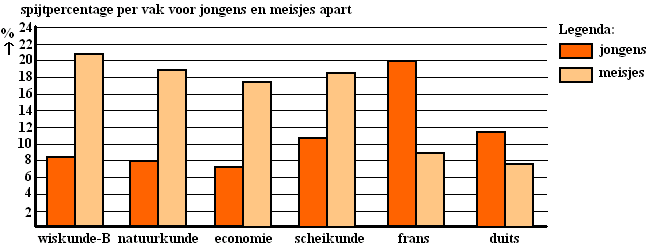
De leerlingen moesten ook aangeven wélke vakken ze zouden willen vervangen.
Voor enkele vakken staat het resultaat in de figuur hieronder. Bijvoorbeeld: van alle meisjes met wiskunde B zou ongeveer 21% dat vak achteraf liever niet hebben gekozen.
       

       
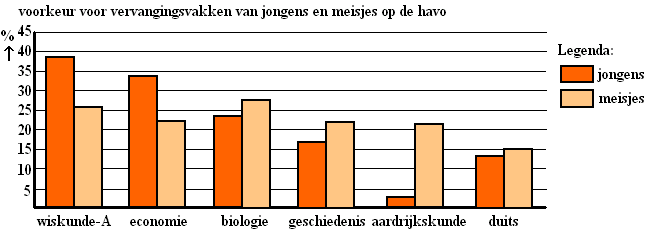
Aan de leerlingen die tenminste één ander vak gekozen zouden hebben werd ook gevraagd welk nieuw vak of welke nieuwe vakken ze zouden kiezen. In de figuur hieronder staat voor enkele vakken het resultaat. Bijvoorbeeld: van de meisjes die tenminste één ander vak gekozen zouden hebben zou ruim 25% wiskunde A kiezen. (Merk op dat veel leerlingen meer dan één nieuw vak zouden kiezen, waardoor het totaal zelfs over deze zes vakken al ver boven de 100% komt).
       

       
Er waren 127 jongens en 232 meisjes die tenminste één ander vak zouden kiezen.
Stel dat alle leerlingen het achteraf gewenste pakket hadden gekozen.
       
7p. 4. Onderzoek of dan nog steeds meer meisjes dan jongens economie zouden doen. Maak hierbij gebruik van de resultaten van vraag 1 en van de beide figuren hierboven.
       
OPGAVE 2. Kavelkosten.
         
Een gemeente wil uitbreiden door het bouwen van een nieuwe wijk. De plaats waar de nieuwe wijk gebouwd zal worden is vastgesteld. Voordat de gemeente het uitbreidingsplan laat uitvoeren doet de gemeente onderzoek naar de kosten van het plan. Er zijn twee soorten kosten voor de gemeente:
• de kosten van aankoop van de grond. In deze situatie bedragen de kosten 170000 gulden per hectare (1 hectare = 10000 m2)
• de kosten van het bouwrijp maken. Dit betreft kosten voor de aanleg van bijvoorbeeld wegen, rioleringen en groenvoorzieningen. Deze kosten zijn hoger naarmate het aantal woningen dat per hectare gebouwd zal worden groter is.
         
In de figuur hieronder zijn kosten van diverse vergelijkbare projecten door middel van plusjes weergegeven. Zowel langs de horizontale as als langs de verticale as is een logaritmische schaalverdeling gebruikt. Hierbij is x het aantal woningen per hectare. B stelt voor de kosten per hectare van het bouwrijp maken in duizenden guldens. Op grond van de plusjes in de figuur is een kromme getekend die het verband tussen x en B weergeeft.
         

         
De formule die bij dit verband tussen B en x hoort is van de vorm  B = p • xq
         
6p. 5. Kies tenminste 4 punten van de grafiek (de kromme) in deze figuur. Teken deze punten op dubbellogaritmisch papier en leg uit waarom het verband tussen B en x inderdaad van de vorm B = p • xq kan zijn.
         
6p. 6. Bereken p en q in twee decimalen nauwkeurig.
         
Ga er in de rest van de opgave van uit dat  B = 0,4 · x1,8

Neem aan dat de gemeente 30 woningen per hectare wil bouwen.
         
4p. 7. Bereken de totale kosten die de gemeente dan per woning zal maken.
         
De totale kosten per woning die de gemeente maakt noemen we K. Voor het verband tussen K en x kan de volgende formule worden afgeleid:    K = 0,4 · x0,8 +  170/x
Hierbij is K in duizenden guldens.
         
2p. 8. Toon dit aan.
         
De gemeente wil dat de kavelgrootte (dat wil zeggen de grondoppervlakte) voor alle woningen hetzelfde is. Bovendien wil men dat de totale kosten die de gemeente per woning maakt minimaal zijn. Dit is het geval bij ongeveer 32,7 woningen per ha.
         
5p. 9. Stel een formule op voor de afgeleide van K en toon met behulp daarvan aan dat de totale kosten inderdaad minimaal zijn bij ongeveer 32,7 woningen per ha.
         
OPGAVE 3.  Kantine.
         
In de kantine van een bedrijf worden twee warme lunches aangeboden: een 'exotische lunch' en een 'Hollandse lunch'. De kantinebeheerder mag hiervan zelf de prijs bepalen. De beheerder merkt dat de verkoopprijs van één maaltijd van invloed is op de verkochte aantallen van beide maaltijden. We nemen aan dat het volgende stelsel vergelijkingen is op te stellen voor het verband tussen de verkoopprijzen en de aantallen verkochte maaltijden:
         

         
Hierbij is a het aantal verkochte exotische lunches per maand en b het aantal verkochte Hollandse lunches per maand. Verder is x de verkoopprijs (in guldens) van de exotische lunch en y de verkoopprijs (in guldens ) van de Hollandse lunch.

De totale kosten die de beheerder maakt zijn ƒ3,- voor een exotische lunch en ƒ2,- voor een Hollandse lunch.

De beheerder wil weten hoe groot de winst is als een exotische lunch voor ƒ3,25 en een Hollandse lunch voor ƒ2,25 verkocht wordt.
         
4p. 10. Bereken in deze situatie de winst per maand op exotische lunches en de winst per maand op Hollandse lunches.
         
TK zijn de totale kosten per maand in guldens. W is de totale winst per maand in guldens. TK zowel als W kunnen worden uitgedrukt in x en y:
         
    TK = 500y - 4000x + 17500
W = -3000x2 + 6000xy + 6500x + 4500y - 17500
         
4p. 11. Toon de juistheid van de formule voor W aan. Gebruik daarbij eventueel de bovenstaande formule voor TK.
         
Het stelsel vergelijkingen voor het verband tussen x , y, a en b is slechts geldig voor  a ≥ 0 en  b ≥ 0. Bovendien worden de maaltijden niet verkocht onder de kostprijs dus x ≥ 3 en  y ≥ 2. Deze beperkingen leiden ertoe dat het hierboven omschreven model (het stelsel vergelijkingen voor het verband tussen x, y, a en b) slechts geldig is op een beperkt gebied voor x en y.
         
7p. 12. Teken dit toegestane gebied in een xy- assenstelsel.
         
Het doel van de beheerder is om de verkoopprijzen zodanig vast te stellen dat zijn maandelijkse winst zo hoog mogelijk is.

De beheerder rekent, uitgaande van de formule voor W, eerst een getallenvoorbeeld door.
Hij kiest y = 3
         
5p. 13. Bereken bij welke verkoopprijs van een exotische lunch de winst in dat geval zo hoog mogelijk is.
         
In de tabel hieronder is voor een aantal andere keuzes voor y af te lezen bij welke verkoopprijs van een exotische lunch de winst zo hoog mogelijk is. Ook is steeds die hoogste winst berekend.
         
keuze y beste x getallenpaar (x,y) W
2,10 3,18 (3.18 ; 2,10) 300,80
2,20 3,28 (3.28 ; 2.20) 540,80
2,25 3,33 (3.33 ; 2.25) 645,80
         
In de hierna volgende tabel is voor een aantal keuzes van x af te lezen bij welke verkoopprijs van een Hollandse lunch de winst zo hoog mogelijk is. Ook hier is steeds die hoogste winst berekend.
         
keuze x beste y getallenpaar (x, y) W
3,10 2,31 (3.10 ; 2.31) 500,50
3,20 2,37 (3.20 ; 2.37) 664,50
3,30 2,43 (3.30 ; 2.43) 804,50
         
De punten die horen bij de getallenparen (x,y) uit de eerste tabel liggen op een rechte lijn. Ook de punten die horen bij de getallenparen (x,y) uit de tweede tabel liggen op een rechte lijn.
Het snijpunt van deze twee lijnen levert de verkoopprijzen met maximale winst.
         
6p. 14. Bereken nu de maximale winst voor de beheerder.
         
OPGAVE 4. Apen.
         
Biologen hebben onderzoek gedaan naar het contact tussen moeder en kind bij resusapen. Daartoe observeerden ze één moeder en haar kind gedurende langere tijd. Men onderscheidde daarbij drie toestanden:
• bij de moeder (er is lichaamscontact maar het kind is niet aan de borst), afgekort "bij";
• aan de borst,  afgekort "borst";
• los van de moeder (er is geen lichaamscontact tussen moeder en kind), afgekort "los".
         
De biologen registreerden tijdens het onderzoek nauwkeurig welke overgangen er tussen deze toestanden voorkwamen. Zo ontstond een rij waarnemingen. Het begin en het eind van deze rij zie je hieronder in beeld gebracht:
         

bij  →  los  →  borst  →  borst  →  .....  →  los  →  bij
         
Zoals je ziet kwam het voor dat een toestand overging in dezelfde toestand. Dit gebeurde bijvoorbeeld als de moeder het kind van de borst wilde halen en het kind daartegen protesteerde en weer terug aan de borst ging.
In de volgende figuur zie je de aantallen overgangen tijdens het onderzoek in een graaf aangegeven.
         

         
Wanneer we bij de toestand "borst" de getallen bij de uitgaande pijlen optellen, dan vinden we dezelfde uitkomst als wanneer we de getallen bij de aankomende pijlen bij "borst" optellen. Dit geldt ook voor de andere twee toestanden.
         
4p. 15. Verklaar met de gegeven rij waarnemingen waarom in de graaf bij iedere toestand de som van de getallen bij de uitgaande pijlen gelijk is aan de som van de getallen bij de aankomende pijlen.
         
Bij deze graaf kunnen we onderstaande overgangsmatrix M maken. De getallen in M zijn afgerond op drie decimalen.
         
         
3p. 16. Laat met een berekening zien hoe uit de gegevens van de graaf het getal 0,652 in deze matrix tot stand is gekomen.
         
Met behulp van de graaf kunnen we ook berekenen hoe vaak tijdens het onderzoek een bepaalde toestand voorkwam. Je vindt die aantallen in onderstaande kolommatrix P. Hierbij zijn begin- en eindtoestand van het onderzoek als één toestand gezien.
         
3p. 17. Bereken M × P en geef de elementen van deze matrix in 3 decimalen nauwkeurig.
         
De biologen hielden ook bij hoe lang elke toestand duurde. Uit het onderzoek bleek dat de tijdsduur van de verschillende toestanden varieerde. De totale tijdsduur van de toestand "bij" was 685 sec. De totale tijd in de toestand "borst" was 876 sec. en de totale tij in de toestand "los" 2019 sec.
De biologen wilden dit onderzoek gebruiken om te komen tot een kansmodel voor het gedrag van resusapen. Ze bepaalden bijvoorbeeld met behulp van de resultaten van het onderzoek de kans op de toestand "borst". Eén van de biologen merkte op dat je dit op twee manieren kunt doen.
Manier I: In de rij waarnemingen boven aan deze opgave kun je willekeurig een toestand aanwijzen en dan kijken hoe groot de kans is dat dit de toestand "borst" is.
Manier II: Je kunt een willekeurig moment aanwijzen in de observatieperiode (die op video is vastgelegd) endan kijken hoe groot de kans is dat dit de toestand "borst" is.
         
6p. 18. Bereken beide kansen.
         
De biologen kozen ervoor om kansen te bepalen uitgaande van manier II. In het verslag van het onderzoek werd melding gemaakt van de kans dat een willekeurige toestand gevolgd werd door dezelfde toestand. Hierbij stond onderstaande figuur afgedrukt.
         

         
6p. 19. Bereken de kans dat een via manier II aangewezen willekeurige toestand wordt gevolgd door dezelfde toestand.
         

 

 

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.  
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.