VWO WA, 2001 - I

 

OPGAVE 1.  Kwaliteitscontrole.
       
In een fabriek worden plastic zakken gevuld met suiker. De vulmachine staat afgesteld op 510 gram. Neem aan dat het gewicht van de zakken suiker normaal verdeeld is met een gemiddelde m van 510 gram en een standaarddeviatie s van 4 gram.
       
3p. 1. Bereken hoeveel procent van alle zakken een gewicht minder dan 500 gram zal hebben.
       
Om de kwaliteit van het vulproces te bewaken, wordt elk uur een aselecte steekproef van 5 zakken suiker genomen. Van elke zak noteert men het gewicht. Ook wordt van de steekproef het totale gewicht T berekend.
       
5p. 2. Bereken de kans dat het totale gewicht van de steekproef minder is dan 2525 gram.
       
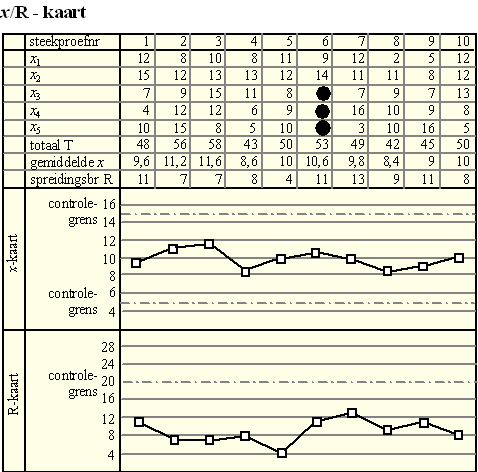
Verder bepaalt men van elke steekproef het gemiddelde gewicht  x en de spreidingsbreedte R (dat is het verschil tussen de grootste en de kleinste meting). Men noteert al deze gegevens op een controlekaart, de x/R-kaart. Op de x/R-kaart hieronder staan de meetresultaten van 10 steekproeven.
Iedere steekproef bestaat uit 5 zakken. Op de controlekaart worden de afwijkingen van 500 gram bij ieder van deze vijf zakken genoteerd als x1, x2, x3, x4 en x5.
Zo heeft de derde zak van de tweede steekproef  een gewicht van 509 gram. Dit is genoteerd als 9.
Het gemiddelde van de eerste steekproef is 509,6 gram. Dit wordt dan genoteerd als 9,6.
De spreidingsbreedte van de eerste steekproef is 515 - 504 = 11 gram.
       

       
Bij steekproef nummer 6 zijn enkele gegevens onleesbaar geworden.
       
3p. 3. Welke getallen kunnen hier bijvoorbeeld gestaan hebben? Licht je antwoord toe.
       
Bij de controle van het vulproces met behulp van de xR-kaart let men erop of x of R de zogeheten controlegrenzen overschrijden. Deze controlegrenzen zijn in de grafieken met stippellijnen aangegeven. Zodra bij een steekproef een van deze grenzen overschreden wordt, slaat men alarm.
Op een gegeven moment slaat men alarm bij een steekproef terwijl met de waarde van x niets mis is.
       
4p. 4. Wat zouden de vijf gewichten in deze steekproef bijvoorbeeld kunnen zijn? Licht je antwoord toe.
       
De bij de controles gebruikte zakken legt men in een bak om ze later met de hand in dozen te verpakken. Aan het eind van een dag liggen er 50 zakken in de bak. Daarvan hebben 30 een Nederlandse opdruk en 20 een Arabische opdruk (bestemd voor de export).
Een werknemer zet twee dozen voor zich, een voor de Nederlandse zakken en een voor de Arabische. In elke doos passen 10 zakken. Hij pakt telkens aselect een zak uit de bak en doet die in de goede doos. Zodra hij een doos vol heeft plakt hij die dicht, en neemt hij zo nodig een nieuwe.
       
5p. 5. Bereken de kans dat hij na 10 zakken al een doos vol heeft. Geef je antwoord in vier decimalen nauwkeurig.
       
De zakken zijn bedrukt met het bedrijfslogo. Soms is dit logo onscherp afgedrukt. Volgens de afdeling Verpakkingen heeft 54% van de zakken een onscherp logo. Een werknemer van die afdeling vermoedt echter dat dit percentage hoger is dan 5%. Er wordt een steekproef getrokken van 50 zakken. Op 6 van de 50 zakken is het bedrijfslogo onscherp.
       
5p. 6. Onderzoek of de zes zakken met het onscherpe bedrijfslogo voldoende aanleiding zijn om de werknemer in het gelijk te stellen. Neem als significantieniveau α = 0,025.
       
OPGAVE 2.  Verleiding.
         
De Corynopoma riisei is een Zuid-Amerikaanse vis. Begin jaren zestig heeft K. Nelson onderzoek gedaan naar het paringsgedrag van deze visjes. Hij ontdekte dat het mannetje verschillende bewegingen uitvoert, zonder vaste volgorde, terwijl het vrouwtje daar een tijd lang niet op reageert. De bewegingen die Nelson onderscheidde zijn:
• Achtervolgen: het mannetje achtervolgt het vrouwtje;
• Vinvertoon: het mannetje zet zijn rugvin op;
• Knikken:  het mannetje maakt een heen en weer gaande beweging;
• Trillen: het mannetje maakt een snel trillende beweging;
• Omstrengelen: het mannetje omstrengelt het vrouwtje.
         
In de onderstaande figuur zijn de overgangskansen tussen de bewegingen af te lezen. Zo gaat het mannetje nadat het gestopt is met achtervolgen in 70% van de gevallen even later weer achtervolgen. In 30% van de gevallen gaat het mannetje over op vinvertoon.
         

         
Een mannetje is bezig met achtervolgen. Hierna zou de volgende reeks bewegingen kunnen voorkomen:
vinvertoon - knikken - trillen - omstrengelen.
         
5p. 7. Bereken de kans dat het mannetje na het achtervolgen inderdaad deze reeks bewegingen uitvoert.
         
In de figuur hierboven is te zien dat niet alle overgangen voorkwamen. Zo kwam na omstrengelen nooit knikken.
De volgende directe-wegenmatrix is opgesteld:
         

         
Het kwadraat van M is de matrix:
         

         
Na achtervolgen kan een mannetje de bij vraag 7 vermelde reeks bewegingen uitvoeren, maar er zijn ook allerlei andere mogelijkheden.

Een mannetje is bezig met achtervolgen.
         
6p. 8. Bereken hoeveel verschillende reeksen van vier bewegingen het mannetje hierna kan uitvoeren, met als laatste beweging omstrengeling.
         
Naast de directe-wegenmatrix M is ook een 5´5 overgangsmatrix A te maken:
         

         
2p. 9. Geef de vierde kolom van deze matrix.
         
Hieronder is matrix A25 gegeven. De elementen zijn afgerond op drie decimalen.
         

         
Als we uitgaan van 1000 mannetjes die alle bezig zijn met achtervolgen, dan kan de toestand van deze 1000 mannetjes beschreven worden met de matrix:
         

         
Als we deze 1000 mannetjes gedurende 25 bewegingen volgen, dan mogen we op grond van de matrix A25 verwachten dat bij de laatste beweging 509 mannetjes bezig zijn met achtervolgen, 405 bezig zijn met vinvertoon, 56 met knikken, 22 met trillen en 8 met omstrengelen.
         
3p. 10. Toon dit met een berekening aan.
         
We gaan voor de volgende vraag uit van een willekeurige groep van 1000 mannetjes. Ook deze groep volgen we gedurende 25 bewegingen. Het is aan te tonen dat een dergelijke groep, ongeacht de beginsituatie, naar verwachting na 25 bewegingen altijd dezelfde verdeling zal vertonen, namelijk 509 mannetjes bezig met achtervolgen, 405 bezig met vinvertoon, 56 met knikken, 22 met trillen en 8 met omstrengelen.
         
4p. 11. Toon aan dat we voor iedere groep van 1000 mannetjes na 25 bewegingen nar verwachting inderdaad deze verdeling zullen vinden.
         
OPGAVE 3.  Koeling.
         
Wageningse onderzoekers hebben zich verdiept in de groei van het aantal bacteriën in voedsel. Bij constante bewaartemperatuur groeit het aantal bacteriën exponentieel. De bijbehorende groeifactor hangt af van die bewaartemperatuur. Bij een krantenartikel hierover stond de volgende grafiek.
         

         
In de grafiek wordt de bacteriegroei beschreven in kip die eerst vijf dagen lang bij de producent bij een temperatuur van 0ºC wordt bewaard, en vervolgens in de winkel bij 0ºC (winkel A) respectievelijk 4ºC (winkel B) wordt bewaard.
         
4p. 12. Toon aan dat bij 0ºC het aantal bacteriën zich per dag meer dan verdubbelt.
         
In de figuur hierboven is het aanvankelijke aantal bacteriën per gram gelijk aan 1000. De bederfgrens ligt bij 50 miljoen bacteriën per gram. In de figuur is af te lezen dat kip die voortdurend bij 0ºC wordt bewaard, na 14 dagen de bederfgrens bereikt.

Stel dat men in staat is het aanvankelijke aantal bacteriën terug te brengen van 1000 per gram naar 100 per gram. Dit verlengt de houdbaarheid natuurlijk. Voor winkel A duurt het drie dagen langer voordat de bederfgrens bereikt wordt. Voor winkel B, waarbij de kip eerst gedurende vijf dagen bij 0ºC bewaard wordt en daarna bij een temperatuur van 4ºC, geldt een andere verlengingsduur.  

         
5p. 13. Teken voor deze nieuwe situatie in bovenstaande figuur de grafiek voor de bacteriegroei in kip voor winkel B, en lees af hoeveel langer het nu duurt voordat de bederfgrens is bereikt.
         
Om de grafiek hierboven te tekenen gebruikten de onderzoekers een formule voor het verband tussen de bewaartemperatuur T en de groeifactor per dag g van het aantal bacteriën. Bij het opstellen van deze formule waren zij er van uitgegaan dat bacteriegroei alleen optreedt boven een bepaalde minimumtemperatuur. Deze minimumtemperatuur T0 hangt af van het soort voedsel. Voor elk soort voedsel heeft de formule de volgende vorm:
         

         
In deze formule is T in ºC met T ≥ T0 en is c een constante.

We kunnen controleren dat er volgens deze formule inderdaad geen bacteriegroei optreedt als T = T0.
         
3p. 14. Voer deze controle uit.
         
Uit praktische overwegingen schrijft men de formule voor de groeifactor vaak in de vorm  g = 10m. Deze variabele m is afhankelijk van T. Er geldt  √m = c(T - T0).

Voor elk soort voedsel moeten c en T0 experimenteel bepaald worden. Zo heeft men voor kip bij allerlei bewaartemperaturen de bacteriegroei gemeten. Bij de verwerking van de metingen hebben de onderzoekers het verband tussen T en √m in een grafiek gezet, omdat dit verband volgens de formule lineair is. Het resultaat staat in onderstaande figuur. 

         

         
6p. 15. Leid uit de grafiek van dit lineaire verband benaderingen af voor de constanten c en T0.
         
Ga er in de rest van deze opgave van uit dat geldt:   c = 0,096 en T0 = -6.

In de eerste figuur van deze opgave kunnen we aflezen dat kip met een aantal bacteriën van 1000 per gram bij het begin na 14 dagen de bederfgrens bereikt wanneer die wordt bewaard bij 0ºC.

Het kan echter ook voorkomen dat tijdens het transport een halve dag (12 uur) wordt bewaard bij een temperatuur van 18ºC en daarna steeds bij 0ºC.
         
5p. 16. Hoeveel eerder wordt dan de bederfgrens bereikt? Licht je antwoord toe en gebruik daarbij eventueel de bovenstaande grafieken.
         
OPGAVE 4. Tillen.
         
Veel rugklachten worden veroorzaakt door het (verkeerd) tillen van zware voorwerpen. Het Amerikaanse National Institute for Occupational Safety and Health (NIOSH) heeft een methode ontwikkeld om voor iedere tilsituatie het aanbevolen maximale tilgewicht RWL (Recommended Weight Limit) te bepalen. In de figuur hieronder is zo'n tilsituatie weergegeven.
         

         
In deze figuur is:

H de horizontale afstand in cm van de handen tot de enkels bij het begin van het tillen.
V de verticale afstand in cm van het voorwerp tot de vloer bij het begin van het tillen
D de verticale afstand in cm waarover het voorwerp moet worden getild.

Verder hangt de tilsituatie af van de tilfrequentie  F. Dit is het aantal keren per minuut dat een voorwerp wordt getild.
De RWL (in kg) wordt berekend door 23 kg te vermenigvuldigen met een aantal reductiefactoren die afhangen van de afstanden H, V en D en van de tilfrequentie F.
in een formule:

RWL = 23 · HF · VF · DF · FF
         
Hierin zijn HF, VF, DF en FF de reductiefactoren.

De reductiefactor VF hangt af van de afstand V volgens onderstaande formule:
         

         
3p. 17. Welke waarde van V geeft de grootste waarde van VF? Licht je antwoord toe.
         
De reductiefactoren HF en DF hangen af van de afstanden H en D volgens de formules:
         

         
De reductiefactoren HF, VF, DF en FF zijn allemaal kleiner dan of gelijk aan 1. Als H zo klein is dat HF volgens bovenstaande formule groter zou zijn dan 1, dan wordt de formule voor HF niet gebruikt. In dat geval neemt men HF = 1.
Hetzelfde geldt voor DF:  als D zo klein is dat DF volgens bovenstaande formule groter dan 1 zou zijn, wordt de formule voor DF niet gebruikt. In dat geval neemt men DF = 1.
         
3p. 18. Bereken de kleinste waarde van D waarbij de formule voor DF nog te gebruiken is.
         
De reductiefactor FF hangt af van de tilfrequentie F. Voor het verband tussen F en FF heeft men geen formule opgesteld. In plaats daarvan maakt men gebruik van de waarden in de tabel hieronder.
         
frequentie F
(aantal per minuut)		 <0,2 0,5 1 2 3 4 5 6 7 8 9 10 11 12
FF 1,00 0,97 0,94 0,91 0,88 0,84 0,80 0,75 0,70 0,60 0,52 0,45 0,41 0,37
         
Volgens de NIOSH-methode wordt een tilsituatie veilig genoemd als het gewicht (in kg) van het te tillen voorwerp niet groter is dan de RWL.
Een werknemer moet vijf keer per minuut een krat van een lopende band in een spoelmachine tillen. Er geldt  H = 40 cm, V = 60 cm en D = 30 cm. De kratten wegen 11 kg.
         
6p. 19. Bereken de maximale tilfrequentie waarbij dit volgens de NIOSH-methode nog een veilige tilsituatie is.
         
Een andere werknemer, die op de grond staat, moet dozen van een laadklep op een lopende band zetten met een frequentie van 1 doos per 5 minuten. Er geldt H = 25 cm. De hoogte van de laadklep kan ingesteld worden tussen 75 cm en 165 cm. De lopende band bevindt zich op een hoogte van 190 cm.
         
4p. 20. Toon aan dat in deze situatie met de laadklep geldt:  VF = 0,003D + 0,655
         
De formule voor de RWL is nu te herleiden tot:

         
Het ligt voor de hand te denken dat in deze situatie de RWL kleiner is naarmate de laadklep lager staat, dus naarmate D groter is. Toch blijkt dat volgens de formule niet zo te zijn.
         
5p. 21. Stel de afgeleide van RWL op en bereken daarmee voor welke waarde van D de RWL minimaal is.
         

 

 

UITWERKING
   
1.  
   
2.  
   
3.  
   
4.  
   
5.  
   
6.  
   
7.  
   
8.  
   
9.  
   
10.  
   
11.  
   
12.  
   
13.
   
14.  
   
15.  
   
16.  
   
17.  
   
18.  
   
19.  
   
20.  
   
21.  
   
22.  
   
23.