Nieuwe pagina 1

OPGAVE 1. Woningen.

In 1984 vond een onderzoek plaats naar energieverbruik in woningen in Nederland. In deze opgave komen verschillende zaken uit dat onderzoek aan de orde. Bij het onderzoek waren 6000 aselect gekozen woningen betrokken.

Gasverbruik en muurisolatie.

Uit de 6000 woningen heeft men een aselecte steekproef van 50 woningen getrokken. Men is deze 50 woningen langsgegaan om te vragen of de woning voorzien was van muurisolatie. Van deze 50 woningen bleken er 29 geen muurisolatie te hebben. De gegevens over het gasverbruik in deze 29 woningen zijn verwerkt in een cumulatieve frequentiepolygoon (in procenten). Zie de volgende figuur. De klassebreedte is 1000 m³.

4p.

Bereken in hoeveel van deze 29 woningen het gasverbruik lag tussen 3000 m³ en 4000 m³ per jaar.

In de volgende tabel is het gasverbruik per jaar vermeld van de 21 woningen uit de steekproef die wel muurisolatie hadden.

Gasverbruik per jaar in elk van de 21 woningen met muurisolatie.
nummer aantal m³	1 194	2 351	3 407	4 452	5 1308	6 1351	7 1369	8 1380	9 1432	10 1650	11 1803
nummer aantal m³	12 1954	13 2288	14 2761	15 2850	16 3409	17 3744	18 3912	19 4164	20 4782	21 7051

5p.

Teken in de figuur hierboven een cumulatieve frequentiepolygoon (in procenten) voor het gasverbruik per jaar in de 21 woningen met muurisolatie. Licht je werkwijze toe.

Voordat het onderzoek had plaatsgevonden, veronderstelde men dat ten minste de helft van de woningen in 1984 muurisolatie had.

5p.

Ga na of de uitslag van de steekproef van 50 woningen bij een significantieniveau van 5% voldoende reden vormt om deze veronderstelling te herzien.

Bouwjaar en bewoner.

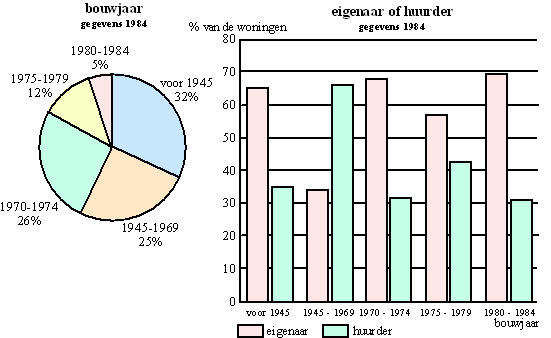
In verband met subsidies heeft men nagegaan hoeveel van de 6000 woningen in 1984 door de eigenaar werden bewoond. Daarbij lette men ook op het bouwjaar van de woningen. De volgende twee figuren geven de resultaten weer.

4p.

Bereken met behulp van de figuren hoeveel procent van de woningen ten tijde van het onderzoek bewoond werd door de eigenaar.

Elektriciteitsverbruik.

Uit de gegevens van de 6000 woningen bleek:

•

in 30% van de woningen werd voor warm water gebruik gemaakt van elektriciteit; het elektriciteitsverbruik binnen deze groep woningen was bij benadering normaal verdeeld met een gemiddelde van 4500 kWh en een standaarddeviatie van 1000 kWh.

•

in 70% van de woningen werd voor warm water gebruik gemaakt van gas; het elektriciteitsverbruik binnen deze groep was bij benadering normaal verdeeld met een gemiddelde van 2500 kWh en een standaarddeviatie van 750 kWh.

6p.

Bereken bij hoeveel procent van de woningen het elektriciteitsverbruik minder was dan 2500 kWh.

OPGAVE 2. Reizen in de spits.

In de spits zijn files en langzaam rijdend verkeer normale verschijnselen geworden. De aanleg van extra wegen en het wegnemen van knelpunten lijken voor de hand liggende oplossingen. In deze opgave blijkt dat zulke oplossingen soms verrassende gevolgen hebben. Als model nemen we een situatie waarin 10000 reizigers zich tijdens de spits moeten verplaatsen van stad D naar stad E. Zij kunnen dat doen met de sneltram of met hun eigen auto (één persoon per auto). Op de autoroute is een brug een belangrijk knelpunt. Zie de volgende figuur.



We letten alleen op reistijden. De reistijd (T₁) in minuten van D naar E per sneltram hangt af van het aantal passagiers (p). Bij een groter passagiersaanbod worden er meer trams ingezet. Dit heeft tot gevolg dat de reistijd afneemt doordat de daarin verwerkte wachttijd minder wordt. T₁ kan benaderd worden met de formule T₁ = 20 - 0,0005p. De reistijd (T₂) in minuten van D naar E per auto hangt af van de capaciteit van de brug en van het aantal reizigers (a) dat van de auto gebruik maakt. T₂kan benaderd worden met de formule T₂ = 5 + c • a . Hierbij is c een constante die kleiner is naarmate de capaciteit van de brug groter is. Aanvankelijk geldt c = 0,0052. Stel eens dat 6000 van de 10000 reizigers gebruik maken van de sneltram.

4p.	6.	Bereken de reistijd per sneltram en de reistijd per auto.

Iedere reiziger streeft naar een zo kort mogelijke reistijd voor zichzelf. Dit heeft tot gevolg dat er op den duur een evenwichtssituatie ontstaat waarbij de reizigersstroom zodanig over de twee keuzemogelijkheden verdeeld is dat de twee reistijden even groot zijn. In de evenwichtssituatie maken 7872 van de 10000 reizigers gebruik van de sneltram. Ook in deze evenwichtssituatie zullen er toch voortdurend reizigers zijn die de volgende dag een ander vervoermiddel nemen. Dit kan worden weergegeven in de volgende graaf:



Hierin zijn x en y overgangskansen. Neem aan dat in deze evenwichtssituatie dagelijks in totaal 200 reizigers een ander vervoermiddel kiezen dan de vorige dag.

4p.	7.	Bereken de overgangskansen x en y in vier decimalen nauwkeurig.

In de figuur hieronder zijn de reistijd per tram (T₁) en de reistijd per auto (T₂) uitgezet tegen de reizigersaantallen.



De brug wordt verbreed, waardoor c afneemt van 0,0052 naar 0,0016. Meer reizigers zullen daardoor kiezen voor de auto. Op den duur zal er een nieuwe evenwichtssituatie ontstaan met weer gelijke reistijden voor alle reizigers. Het verrassende hierbij is echter dat iedereen in de nieuwe evenwichtssituatie een langere reistijd heeft dan voorheen!

3p.	8.	Verklaar het bovenstaande met behulp van de figuur.

5p.	9.	Bereken de nieuwe reistijd.

Bovenstaand effect staat bekend als de paradox van Downs-Thomson. De paradox ontstaat doordat iedere reiziger alleen maar op zijn eigen reistijd let bij het kiezen van het vervoermiddel. Bij zijn keuze speelt geen rol dat hij andere reizigers extra reistijd kan aandoen. Het zou beter zijn als de reizigersstroom zich zo zou verdelen dat de totale reistijd van alle reizigers samen (T_totaal) minimaal is. In dat geval is immers de gemiddelde reistijd per reiziger zo klein mogelijk.

4p.	10.	Toon aan dat T_totaal als volgt kan worden uitgedrukt in c en a : T_totaal = (c - 0,0005)a² - 5a + 150000 (T_totaal in minuten)

Voor de verbreding van de brug was T_totaal minimaal als 532 reizigers met de auto gingen. De minimale waarde van T_totaal was in dat geval 148670 minuten. De minimale waarde van T_totaal na verbreding van de brug is kleiner dan de minimale waarde van T_totaal voor de verbreding.

4p.	11.	Toon dit met behulp van een berekening aan.

OPGAVE 3. Zagen.

Meubelfabriek ZFP heeft een volautomatische zaagmachine. Hiermee worden stoelzittingen uit platen van geperst en verlijmd hout gezaagd. De machine kan in drie standen zagen: langzaam, matig en snel. Als er sneller gezaagd wordt, kunnen er minder zittingen uit een plaat worden gemaakt. Zie de volgende tabel.

Verzagen van 1 plaat.
stand	langzaam	matig	snel
zaagtijd per plaat in minuten	24	12	6
aantal zittingen per plaat	12	8	5

De zaagmachine kan per week ten hoogste 34 uur gebruikt worden. De platen zijn afkomstig van een toeleveringsbedrijf. Dit bedrijf kan per week ten hoogste 180 platen leveren.
De platen kosten f 8,- per stuk.
Het zagen kost in elke stand f220,- per uur.
De totale fabricagekosten zijn de kosten van de gebruikte platen plus de kosten van het zagen.
Na het uitzagen van de zittingen zijn de restanten van de platen waardeloos.

In de huidige situatie worden er elke week 1320 zittingen gemaakt. Daarbij verzaagt men 20 platen per week in de stand 'langzaam' en 100 platen in de stand 'matig'. De dan nog ontbrekende zittingen worden gemaakt uit platen die in de stand 'snel' verzaagd worden.

5p.

12.

Bereken hoe hoog de wekelijkse totale fabricagekosten zijn.

De bedrijfsleider van ZFP wil nagaan of de kosten met een ander zaagprogramma kunnen worden verminderd. De bedrijfsleider steltwel als eis dat er ook in de nieuwe situatie elke week precies 1320 zittingen worden gemaakt.
De bedrijfsleider gaat uit van een zaagprogramma waarin per week x platen in de stand 'langzaam', y platen in de stand 'matig' en z platen in de stand 'snel' worden verzaagd.

3p.

13.

Verklaar waarom geldt: z = 264 - 2,4x - 1,6y.

Door de formule van vraag 13 kan de bedrijfsleider het probleem behandelen als een lineair programmeringsprobleem met de variabelen x en y.

4p.

14.

Laat zien hoe uit het gegeven over de toelevering volgt: 7x + 3y ≥ 420

Behalve 7x + 3y ≥ 420 en x ≥ 0 en y ≥ 0 zijn er nog twee beperkende voorwaarden voor x en y uit de andere gegevens in de bovenstaande tekst af te leiden.

6p.

15.

Leid uit de andere gegevens in de bovenstaande tekst deze twee overige beperkende voorwaarden voor x en y af en herleid ze tot de vorm ax + by ≤ c

OPGAVE 4. Sinaasappels.

Twee studenten van de Stetson University hebben het verband onderzocht tussen de jaarlijkse aanvoer van sinaasappels in Florida en de gemiddelde veilingprijzen voor die sinaasappels. Dit leidde tot een model waarmee voorspellingen gedaan kunnen worden over de jaaropbrengst.
Uitgangspunt voor hun model waren de gegevens van de volgende tabel.

Jaarlijkse aanvoer en gemiddelde prijs per kist
aantal kisten in miljoenen	Gemiddelde prijs per kist in dollarcents.
45,6 72,5 82,7 98,9 129,7 139,2 169,7	485 287 266 187 157 121 78

De studenten constateerden op grond van de gegevens van deze tabel dat de gemiddelde prijs (P) per kist in dollarcents bij benadering exponentieel afhankelijk is van het aantal miljoenen kisten (A).

5p.

17.

Laat met behulp van logaritmisch papier zien dat deze constatering juist is.

Wanneer er van uit wordt gegaan dat er een exponentieel verband bestaat tussen A en P en dat de grafiek door de punten (75, 300) en (160,90) gaat, kan de gemiddelde prijs per kist bij een aanvoer van 50 miljoen kisten berekend worden.

6p.

18.

Bereken deze prijs in dollarcents nauwkeurig.

In hun model namen de studenten de volgende formule voor het verband tussen A en P aan: P = 841 • e^-0,0136A
Gebruikmakend van dit verband tussen aanvoer en prijs konden zij de maximale jaaropbrengst van de sinaasappels berekenen.

6p.

19.

Bereken hoe groot de maximale jaaropbrengst volgens hun model is. Geef het antwoord in miljoenen dollars nauwkeurig.

UITWERKING

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

VWO WA, 1996 - II