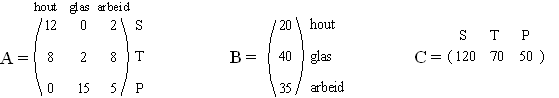OPGAVE 1.
Een fabrikant van tuinbenodigdheden brengt bouwpakketten op de markt voor schuurtjes (S), tuinhuisjes (T) en plantenkassen (P). De benodigde hoeveelheden houten planken in m2, glas in m2 en arbeid in uren voor elk van de drie artikelen is af te lezen uit de matrix A. De kosten van grondstoffen en arbeid in guldens per eenheid zijn af te lezen uit de kolommatrix B. De bestelde aantallen bouwpakketten S, T en P zijn af te lezen uit matrix C.
	a.	Bereken het matrixproduct CAB.  Wat is de betekenis hiervan?
De fabrikant heeft 2200 m2 hout, 510 m2 glas en 850 manuren tot zijn beschikking. Hij is niet in staat deze hoeveelheden aan te vullen.
	b.	Onderzoek of deze hoeveelheden voldoende zijn om aan de vraag volgens de matrix C te kunnen voldoen.
Vanwege de hoge voorraadkosten wil de fabrikant niet meer bouwpakketten produceren dan er besteld zijn. De aantallen bouwpakketten S, T en P stelt hij achtereenvolgens x, y en z.
	c.	De variabelen x, y en z moeten behalve aan de drie voorwaarden x ≥ 0, y ≥ 0 en z ≥ 0 nog aan zes voorwaarden voldoen. Stel deze zes voorwaarden op.
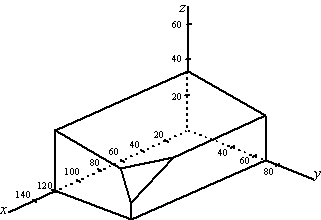
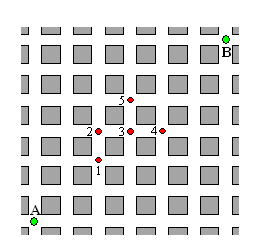
In onderstaande figuur is het toegestane gebied bij de voorwaarden van vraag c) getekend. Dit gebied wordt begrensd door zeven vlakken.
	d.	Bij welke twee van de negen voorwaarden in c) bedoeld, vind je geen grensvlak in de tekening? Verklaar waarom deze twee voorwaarden geen rol spelen.
De winst op een bouwpakket S, T en P is achtereenvolgens f 65,-,  f 130,- en  f 140,-.
	e.	Welke aantallen bouwpakketten S, T en P moet de fabrikant produceren om een zo groot mogelijke winst te maken? Bereken de maximale winst.

OPGAVE 2.
Bij oudheidkundige opgravingen in het Caraïbisch gebied, waar rond 1200 n.C. de Lucayan indianen leefden, werd een groot aantal botresten van vissen opgegraven. Na nauwkeurige bestudering van de botten nam men aan de resten van 150 vissen gevonden te hebben. Met behulp van een bepaald type bot (zie figuur hiernaast) werd de diameter D van zo'n vis geschat. Zo werd de volgende verdeling van diameters gevonden:
	a.	Verwerk deze gegevens in een grafiek op normaal waarschijnlijkheidspapier. Maak daarbij een nieuwe klasse-indeling met een klassebreedte van 1 mm, te beginnen met de klasse waarvan de grenzen zijn 3 en 4. Schat uit deze grafiek het gemiddelde en de standaarddeviatie van de verdeling van D.
Aan de hand van de diameter werd een schatting gemaakt van het gewicht van een vis. Daarbij ging men uit van het verband G = 15D2 , waarbij G = gewicht in g en D = diameter in mm.
	b.	Bereken het aantal vissen met een gewicht van ten hoogste 960 g.
	c.	In een archeologisch artikel werd het verband tussen G en D gegeven door de formule: logG = 2 • logD + 1,18 Toon aan dat deze formule bij benadering gelijkwaardig is met de formule G = 15D2 .
	d.	Iemand beweert dat het gemiddelde gewicht van de vissen kan worden berekend door in de formule G = 15D2 voor D de gemiddelde diameter in te vullen; de zo verkregen waarde van G is dan het gemiddelde gewicht. Onderzoek of deze bewering juist is.
Als het bot dat kenmerkend is voor de diameter van de vis niet gevonden wordt, gebruikt men het totale gewicht van de botresten van een vis om het skeletgewicht te schatten. Het lichaamsgewicht van de vis wordt dan gevonden via de formule  G = 101,5 • S0,8 , waarbij  S = skeletgewicht in g en G = lichaamsgewicht in g.
	e.	Van een vis wordt het skeletgewicht geschat op 80 g. Bereken in één decimaal nauwkeurig de diameter van die vis.
	f.	Een van de onderzoekers heeft een nauwkeurige grafiek gemaakt van G als functie van S. Bereken in één decimaal nauwkeurig de helling van die grafiek in het punt met S = 50.
	g.	Het skeletgewicht S kan worden uitgedrukt in de diameter D met behulp van de formule logS = alogD + b. Bereken a en b in één decimaal nauwkeurig.

OPGAVE 3.
De figuur hiernaast toont de plattegrond van een stadswijk.
	a.	Een inspecteur van politie belast met verkeerscontrole, gaat van post A naar post B en zorgt ervoor dat hij de vijf drukke kruispunten 1, 2, 3, 4 en 5 elk precies één keer en in deze volgorde aandoet. Hij volgt daarbij een zo kort mogelijke weg. Uit hoeveel verschillende routes kan hij kiezen?
Een verkeersagent krijgt de opdracht om op de kruispunten 1, 2, 3, 4 en 5 dienst te doen. Op elk kruispunt oefent hij zijn dienst tenminste één uur uit. Aan het einde van zo'n uur stelt hij vast op welk kruispunt hij het eerstvolgende dienstuur zal zijn. Dat kan óf een naburig kruispunt óf hetzelfde kruispunt zijn.
Om te voorkomen dat hij volgens een vast patroon zijn aandacht over de vijf kruispunten verdeelt, laat hij zijn keus door het toeval bepalen; daarbij heeft elk van de mogelijkheden evenveel kans. Als hij bijvoorbeeld een uur op punt 2 is geweest, dan heeft hij kans 1/3 om het volgende uur op punt 3, 1/3 om op punt 1, en 1/3 om weer op punt 2 te zijn.
	b.	Om 10.00 uur gaat de agent naar kruispunt 5. Hoe groot is de kans dat hij van 12.00 tot 13.00 uur op punt 3 zijn dienst uitoefent?
De elementen van matrix M hiernaast zijn de overgangskansen bij de vijf kruispunten.
	c.	Bereken het element in de tweede rij en de tweede kolom van de matrix M2. Wat is de betekenis van dit getal voor de verkeersagent?
	d.	De matrix M heeft de eigenschap dat de som van de getallen in elke kolom gelijk is aan 1. Beredeneer, zonder de matrix M2 te berekenen, dat M2 dezelfde eigenschap heeft.
De computer van het bureau van de verkeerspolitie heeft een berekening uitgevoerd zoals beschreven in onderstaand structuurdiagram. Daarbij is voor K de kolommatrix met op de eerste plaats een 1 en op de andere vier plaatsen 0 ingevoerd;  M is de gegeven 5 x 5 matrix en  M * K is het matrixproduct van M en K.
Hieronder is een gedeelte van de output afgedrukt. De eindkolommen van deze output zijn onafhankelijk van het kruispunt waar een agent op de eerste dag zijn dienst begint.
	e.	Een verkeersagent met een 40-urige werkweek vervult gedurende 13 weken de dienst op de kruispunten 1, 2, 3, 4 en 5. Hoeveel uur van deze periode zal hij naar verwachting op elk van die kruispunten aanwezig zijn?
	f.	De agent heeft in de genoemde periode 100 verkeersovertredingen waargenomen. In 74 van die gevallen was de betrokken chauffeur een man, in 26 gevallen een vrouw. Uit verkeerspeilingen in die wijk is bekend dat 64% van de auto's door een man wordt bestuurd. Neem aan dat de steekproef van 100 overtredingen aselect is. Ga na of men op grond van deze gegevens de conclusie kan trekken dat in deze stadswijk mannelijke chauffeurs naar verhouding vaker een verkeersovertreding maken dan vrouwelijke chauffeurs. Neem een significantieniveau van 2,5%.

UITWERKING
1a.	f  112350,-
1b.	2000 m2 hout, 890 m2glas, 1050 uur arbeid.
1c.
1d.
1e.	f 19240
2a.	gemiddelde 6,5,  standaarddeviatie 1,3
2b.	134
2c.
2d.	Niet waar
2e.	8,4 mm
2f.	11,6
2g.	a = 2,5  en   b = -0,4
3a.	60
3b.	3/8
3c.	13/36
3d.
3e.	80 - 120 - 160 - 80 - 80
3f.	0,0239, dus H0 verwerpen.