VWO WA, 1984 - I

 

OPGAVE 1.
       
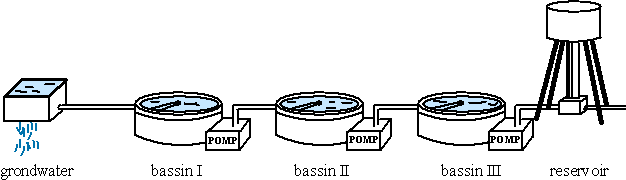
Een waterleidingbedrijf maakt grondwater geschikt voor consumptie door het in drie fases biologisch te zuiveren. Het bedrijf beschikt daartoe over drie bassins I, II en III, waarin achtereenvolgens de eerste, tweede en derde zuivering plaatsvindt.
       

       
Alle drie de bassins zijn gelijktijdig in bedrijf. Na afloop van elke zuiveringsperiode wordt achtereenvolgens water overgepompt van bassin III naar het reservoir, van II naar III, en van I naar II. Daarna wordt een hoeveelheid grondwater in bassin I gebracht. Bij het overpompen van bassin III naar het reservoir, van II naar III en van I naar II blijft steeds 8% van het water in het bassin achter en verdwijnt bij elke pomp 2% van het water in de grond door lekkages van de pomp.
       
  a. Geef de overgangsmatrix voor de drie bassins.
   
       
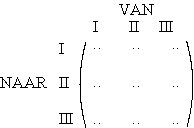  b. Noem de matrix die in vraag a) bedoeld is M.
Beredeneer dat de matrix M2 één nul minder heeft dan M.
       
  c. De matrix M geeft een onvolledig beeld van het proces dat hierboven beschreven is. Maak een gerichte graaf met vijf punten die dit proces wél volledig weergeeft. Vermeld passende percentages bij de pijlen die vanuit de punten I, II en II vertrekken.
       
  d. Veronderstel dat na een zuiveringsperiode en voor het overpompen aanwezig is:
x m3 in I.
y m3 in II.
z m3 in III.
Na het overpompen wordt 5290 m3 grondwater in I gebracht.
Bereken, uitgedrukt in x, y en z, hoeveel m3 water dan in elk van de bassins is.
       
Het zuiveringsproces heet stationair als elke keer dezelfde hoeveelheid grondwater in I gebracht wordt en ook elke keer evenveel schoon water uit III in het reservoir overgepompt wordt.
       
  e. Bij het stationair zuiveringsproces wordt elke keer 5290 m3 grondwater in I gebracht.
Hoeveel m3 water is er dan elke keer na het overpompen en het inbrengen van grondwater in elk van de bassins I, II en III aanwezig?
       
  f. Het waterleidingbedrijf wil in het stationair zuiveringsproces elke keer 5000 m3 schoon water uit III in het reservoir pompen.
Hoeveel m3 grondwater moet dan elke keer in I gebracht worden?
       
OPGAVE 2.
         
Een grootwinkelbedrijf heeft in zijn assortiment een eigen merk zeeppoeder. Het bedrijf beschikt over een vulmachine met een vulcapaciteit van 7536 kg per dag. Van de door de machine gevulde pakken is het gewicht normaal verdeeld , met een standaardafwijking van 40 gram ongeacht de inhoud. De keuringsdienst van waren eist dat, op één decimaal nauwkeurig, slechts 4,0% van de in de handel gebrachte pakken minder mag bevatten dan op de pakken vermeld staat.
Het bedrijf brengt zeeppoeder op de markt in kleine pakken, waarop vermeld staat dat zij 1 kg zeeppoeder bevatten. De vulmachine is ingesteld op 1070 gram per pak.
         
  a. Onderzoek of aan de eis van de keuringsdienst van waren wordt voldaan.
         
De bedrijfsleiding overweegt om naast kleine pakken met opschrift 1 kg ook gezinspakken met opschrift 2,5 kg op de markt te brengen.
         
  b. Op hoeveel gram per pak moet de vulmachine ingesteld worden voor deze gezinspakken?
         
  c. Neem aan dat het aantal geproduceerde kleine pakken twee maal zo groot is als het aantal gezinspakken.
Hoeveel gezinspakken kunnen er dan maximaal per dag worden geproduceerd?
         
De winst op een klein pak wordt gesteld op f 0,40 en die op een gezinspak  f 1,00. Het bedrijf kan per dag beschikken over verpakkingsmateriaal dat toereikend is voor 5000 kleine pakken en 1500 gezinspakken. Het aantal gezinspakken mag ten hoogste de helft van het aantal kleine pakken zijn.
Noem het per dag geproduceerde aantal kleine pakken x en het aantal gezinspakken y.
         
  d. Stel de voorwaarden op waaraan x en y moeten voldoen en teken het bijbehorende gebied in een coördinatenvlak.
         
  e. Bereken bij welke aantallen kleine pakken en welke aantallen gezinspakken het bedrijf op maximale winst kan rekenen.
         
OPGAVE 3.
         
Door een technische storing in de air-conditioning van een groot gebouw neemt het zuurstofgehalte tijdelijk af.
De technische staf heeft het verloop van het zuurstofgehalte beschreven met het volgende model:
         

         
Hierin is t de tijd in minuten, gerekend vanaf het moment dat de storing begon, en is Z het aantal cm3 zuurstof per liter lucht op tijdstip t. Op het moment t = 0 is het zuurstofniveau normaal.
         
  a. Na verloop van tijd nadert het zuurstofgehalte weer tot het normale niveau. Toon aan dat het gekozen model hiermee in overeenstemming is.
         
  b. Toon aan dat, volgens het model, het zuurstofgehalte op het moment t = 0 begint te dalen.
         
  c. Bereken in het model het tijdstip waarop het zuurstofgehalte minimaal is.
         
  d. Iemand beweert dat het zuurstofgehalte 1 uur na het begin van de storing op 90% van het normale niveau is. Onderzoek of die uitspraak klopt met het model.
         
  e. Teken de grafiek van Z als functie van t voor een periode van 1 uur gerekend vanaf t = 0.
         
  f. De medische staf vindt een zuurstofgehalte van 80% van het normale niveau nog net toelaatbaar. Schat met behulp van de grafiek van Z gedurende hoeveel minuten het zuurstofgehalte ontoelaatbaar laag is.
Bereken in één decimaal nauwkeurig het aantal minuten dat, volgens het model, het zuurstofgehalte ontoelaatbaar lag is.
         
OPGAVE 4.
         
Onderstaande tabel geeft de gemiddelde hoogte aan van een bepaald veld zonnebloemen op verschillende tijdstippen na het ontkiemen. De gemiddelde maximale hoogte die deze zonnebloemen bereiken is 256 cm.
         
 
aantal weken hoogte in cm
2
4
6
8
10
12		 36
98
170
228
251
255

         
t is de tijd in weken na het ontkiemen.
H(t) is de gemiddelde hoogte van deze zonnebloemen in cm op het tijdstip t.
         
  a. Onderzoek of er sprake is van lineaire groei, exponentiële groei of geen van beide.
         
  b.
     
  c. Toon aan dat er een eerstegraads functie is die de functie F redelijk benadert en geef het bijpassende functievoorschrift.
         
  d. Leid uit de resultaten van b. en c. een functievoorschrift van H als functie van de tijd af.
         
  e. Een landbouwkundige wil het effect van een bemestingsmiddel op de groei van zonnebloemen onderzoeken met behulp van een tekentoets. Hij zaait 12 paren zonnebloemen, waarbij hij voor één zonnebloem van elk paar het bemestingsmiddel gebruikt, voor de andere niet.
Vier weken na het ontkiemen meet hij de lengte van alle zonnebloemen.
Resultaat:
         
   
Paar 1 2 3 4 5 6 7 8 9 10 11 12
Zonder bemesting 97 99 98 96 95 98 98 100 97 96 97 93
Met bemesting 102 97 100 99 99 103 101 97 102 98 98 101
         
    Geeft dit resultaat aanleiding om te veronderstellen dat het bemestingsmiddel een positief effect heeft op de groei in de eerste vier weken? Men neemt een significantieniveau van 2,5% aan.
         

 

 

 

 

UITWERKING
   
1a.  
   
1b.  
   
1c.  
   
1d. 0,08x + 5290
0,08y + 0,9x
0,08z + 0,9y
   
1e. 5750 m3 - 5625 m3 - 5503,72 m3
   
1f. 5805,21 m3 - 5679,01 m3 - 5555,56 m3
   
2a. 0.0401, dus JA
   
2b. 2570
   
2c. max. 1600
   
2d.  
   
2e. W = 2876
   
3a.  
   
3b.  
   
3c. Z(10) = 150
   
3d. 1,25 uur
   
3e.  
   
3f. 22,4 minuten
   
4a. geen van beide
   
4b.  
   
4c. F(t) = -0,32t + 1,43
   
4d.  
   
4e. 0,0193 dus wel een positief effect.