VWO WA12,  2002 - II
Speelgoedfabriek
Een speelgoedfabrikant maakt houten poppenhuizen en houten treinen. Voor het vervaardigen van het speelgoed onderscheiden we drie soorten arbeid: zagen, timmeren en verven. Het aantal minuten dat hiervoor nodig is vind je in onderstaande tabel.

soort arbeid tijd (in minuten) nodig
per poppenhuis		 tijd (in minuten) nodig
per trein
zagen 24 15
timmeren 60 40
verven 40 10

Er is ιιn personeelslid belast met zagen, twee met timmeren en ιιn met het verven.
Elk van deze vier personeelsleden kan maximaal 40 uren per week werken.

Het aantal poppenhuizen dat per week gemaakt wordt geven we aan met x. Het aantal treinen dat per week gemaakt wordt geven we aan met y.
Op grond van bovenstaande gegevens kunnen we voor deze variabelen de volgende beperkende voorwaarden opstellen:

I 8x + 5y ≤ 800
II 3x + 2y ≤ 240
III 4x + y ≤ 240
IV x ≥ 0
V y ≥ 0
4p 1. Toon aan dat voorwaarde II volgt uit de gegevens.

 
We gaan er in deze opgave van uit dat de kosten voor het maken van het speelgoed bestaan uit materiaalkosten en arbeidskosten. Aan materiaal kost een poppenhuis 17 euro en een trein ook 17 euro. Ieder personeelslid kost 30 euro per gewerkt uur. Alleen voor de gewerkte uren wordt het personeel betaald.

Alle exemplaren die in een week worden gemaakt worden nog in diezelfde week verkocht. De poppenhuizen worden verkocht voor 97 euro per stuk, de treinen voor 58,50 euro per stuk.

De winst in euro's die wekelijks op het speelgoed wordt gemaakt geven we aan met W.
5p 2. Toon aan dat voor W de volgende formule geldt:  W = 18x + 9y

 
De grenslijnen die horen bij de beperkende voorwaarden zijn getekend in de figuur hieronder. Het toegestane gebied is grijs gemaakt.
6p 3. Bereken de maximale winst die wekelijks kan worden behaald. Gebruik daarbij zonodig de figuur hierboven.

 
Degene die met zagen belast is noemen we hierna de zager.
In de figuur hierboven ligt de grenslijn die op het zagen betrekking heeft geheel buiten het toegestane gebied. Dus in de gegeven omstandigheden kunnen er nooit zoveel poppenhuizen en treinen gemaakt worden dat er voor de zager 40 uren werk per week is.
De zager kan ook heel aardig verven. Hij doet dat net zo vlot als degene die dat normaal doet. Men besluit dat de zager een aantal uren per week beschikbaar moet zijn om te verven. Dit aantal uren noemen we d. Gedurende die tijd is hij niet beschikbaar voor het zagen.
Als gevolg hiervan veranderen de beperkende voorwaarden I en III in:
I:     8x + 5y ≤ 800 - 20d
III:  4x + y ≤ 240 + 6d
De andere drie voorwaarden blijven hetzelfde.

Het hangt nu van de keuze van d af hoe het toegestane gebied eruit ziet.
5p 4. Onderzoek of het mogelijk is d zodanig te kiezen dat het toegestane gebied uitsluitend begrensd wordt door de lijnen x = 0, y = 0 en de grenslijn die betrekking heeft op het timmeren. Gebruik zo nodig de figuur hierboven.

 
Keno
In de Verenigde Staten kun je op veelplaatsen het kansspel Keno spelen. De spelregels en de te winnen prijzen zijn niet overal hetzelfde. We kijken in deze opgave naar ιιn bepaalde vorm waarin het spel gespeeld kan worden. Een lot kost 1 dollar. Op het lot staan de getallen 1 tot en met 80. Om mee te spelen moet je 10 van deze getallen aankruisen. Dat kan op verschillende manieren. In de figuur hieronder zie je daar een voorbeeld van.
4p 5. Bereken hoeveel mogelijkheden er zijn om 10 verschillende getallen op het lot te kiezen.

 
Bij de trekking worden door een trekmachine willekeurig 22 getallen gekozen uit de getallen 1 tot en met 80. Nu gaat her erom hoeveel van de 10 aangekruiste getallen goed zijn. Dat wil zeggen hoeveel er bij de 22 getallen uit de trekkingsmachine zitten. Dit aantal bepaalt de prijs die je wint. Het prijzenschema ziet er als volgt uit:

aantal getallen
goed		 prijs
10 $250.000,-
9 $2.500,-
8 $250,-
7 $25,-
6 $7,-
5 gratis lot
4 gratis lot
3 geen prijs
2 geen prijs
1 gratis lot
0 $5,-


Opvallend is dat je bij 0 goed een prijs wint en bij 2 of 3 goed niet. Hiervoor is gekozen omdat bijvoorbeeld de kans dat 2 getallen goed zijn veel groter is dan de kans dat 0 getallen goed zijn.
6p 6. Bereken de kans dat 0 getallen goed zijn en bereken ook de kans dat 2 getallen goed zijn.

 
Stel dat je ιιn lot koopt. De kans dat je direct een geldprijs wint is ongeveer 5,4% en de kans op een gratis lot ongeveer 39,5%. De kans dat je met dat gratis lot bij de volgende trekking een geldprijs wint is weer 5,4% en de kans dat je opnieuw een gratis lot wint is weer 39,5%. Enzovoort.
6p 7. Bereken de kans dat je zo bij een van de eerste tien trekkingen een geldprijs wint.

 
De maker van een website over dit spel verzamelt al sinds de introductie van dit spel de resultaten van alle trekkingen. Hij houdt ook voortdurend bij hoe vaak elk van de 80 getallen getrokken is in alle trekkingen tot dan toe. Op basis daarvan publiceerde hij op een bepaald moment de tabel hieronder. Uit deze tabel blijkt bijvoorbeeld dat tot dat moment 11 van de 80 getallen ten minste 290 en ten hoogste 299 keer waren getrokken.

aantal keren
getrokken		 aantal getallen
260-269 2
270-279 1
280-289 4
290-299 11
300-309 21
310-319 21
320-329 15
330-339 3
340-349 0
350-359 2


Deze tabel heeft betrekking op een groot aantal trekkingen van telkens 22 getallen. Met behulp van de gegeven in de tabel kunnen we een schatting maken van dit aantal trekkingen. De maker van de website beweerde dat de tabel betrekking had op 1126 trekkingen.
5p 8. Onderzoek of deze bewering in overeenstemming kan zijn met de gegevens uit deze tabel.

 
Ransuilen in Vaes
In 1977 troffen onderzoekers in Vaes een kleine groep ransuilen aan. Vanaf dat moment heeft men ze nauwgezet bestudeerd. Daaruit bleek onder andere dat de ransuilen vroeg in het voorjaar broeden en dat de jongen half juni al,kunnen vliegen. Uit tellingen die steeds eind juni plaatsvonden bleek dat de populatie in omvang toenam. In de volgende tabel staan enige resultaten.
Aantal ransuilen per eind juni
jaar 1977 1989
aantal 20 178


Neem aan dat tussen eind juni 1977 en eind juni 1989 het aantal ransuilen jaarlijks met een vast percentage toenam.
4p 9. Bereken met hoeveel procent per jaar het aantal ransuilen in deze periode toenam.

 
Eind juni 1991 telde men 205 ransuilen. Dat is minder dan volgens de bovenstaande groei verwacht mocht worden. Dit zou verklaard kunnen worden door het feit dat door ransuilen gebruikte broedplaatsen (bestaande holtes in bomen en gebouwen) altijd slechts in beperkte mate aanwezig zijn. Daardoor konden sommige vrouwtjes dat jaar geen broedplaats vinden.

Aanvankelijk dacht een onderzoeker het aantal ransuilen vanaf 1989 goed te kunnen voorspellen met een model van de vorm:

R(t) = a - b • 0,6t

Hierbij is R(t) het aantal ransuilen in jaar t en t het aantal jaren na eind juni 1989.

Hij koos a en b zo dat de formule 178 ransuilen opleverde voor 1989 (t = 0) en 205 ransuilen voor 1991 (t = 2). Zo vond hij voor a de waarde 220,2 en voor b de waarde 42,2.
6p 10. Bereken de waarden van a en b afgerond op twee decimalen.

 
We gebruiken verder in deze opgave de formule:

R(t) = 220,2 - 42,2 • 0,6t

Met deze formule kwam de onderzoeker voor eind juni 1993 uit op (afgerond) 215 ransuilen. Deze voorspelling kwam echter niet uit. Eind juni 1993 bleken er 223 ransuilen te zijn in plaats van de voorspelde 215. Daarom stelde de onderzoeker een nieuw model op dat overeenstemde met de aantallen ransuilen van 1989, 1991 en 1993:


Hierbij is Q(t) het aantal ransuilen in jaar t en t het aantal jaren na eind juni 1989.

Hoewel dit laatste model aanvankelijk beter overeenstemt met de waarnemingen dan het eerste model is het mogelijk dat op den duur het eerste model realistischer is. We vergelijken daarom deze twee modellen.

Zowel R(t) als Q(t) geven voor 1989 (t = 0) het aantal van 178 ransuilen.
In de jaren daarna is soms R(t) groter dan Q(t) en soms Q(t) groter dan R(t).
4p 11. Toon dit aan door de grafieken van R en Q te schetsen voor  0 ≤ t ≤ 5
Bij het eerste model is na 1989 steeds sprake van afnemende stijging. We willen weten of dat bij het tweede model ook zo is.
Hoewel Q(t) alleen voor gehele waarden van t zinvolle voorspellingen van het aantal ransuilen geeft kunnen we Q(t) toch voor niet-gehele waarden van t berekenen. Met behulp van differentiλren is het dan mogelijk de stijging van Q(t) te onderzoeken.
4p 12. Differentieer Q(t).

 
3p 13. Onderzoek of bij Q(t) in de periode tussen 1989 en 2000 steeds sprake is van afnemende stijging. Maak voor dit onderzoek een grafiek van de afgeleide functie van Q.

 
Omdat de tellingen slechts een keer per jaar plaatsvinden is een discreet model geschikter. In plaats van bovenstaande formule voor Q(t) had de onderzoeker voor het tweede model ook een recursieve formule kunnen maken van de volgende vorm:

Hierbij is t het aantal jaren na eind juni 1989.
In deze formule kunnen de constante getallen c en d zo gekozen worden dat de waarden van Nt volgens deze formule bij benadering hetzelfde zijn als de waarden van Q(t).

Zowel bij de formule voor Q(t) als bij de recursieve formule nadert het aantal ransuilen op den duur tot eenzelfde evenwichtswaarde.
5p 14. Bereken d met behulp van deze evenwichtswaarde.

 
Alcohol
Alcohol beοnvloedt de rijvaardigheid. De politie houdt regelmatig alcoholcontroles om automobilisten met een te hoog alcoholpromillage in hun bloed te kunnen bestraffen.

Enkele jaren geleden meende Veilig Verkeer Nederland (tegenwoordig heet deze organisatie 3VO) dat er aan de alcoholcontroles nog wel wat verbeterd zou kunnen worden. Zie het volgende artikel.

VVN: dronken automobilisten ontspringen te vaak de dans
HUIZEN  Veilig Verkeer Nederland (VVN) stoort zich aan de manier waarop de politie omspringt met automobilisten die teveel gedronken hebben. Volgens de organisatie wordt 35 procent van de bestuurders die teveel hebben gedronken niet bestraft omdat de controleapparatuur van de politie te ruim staat afgesteld.
.....
Met meer dan 0,5 promille alcohol in het bloed is een automobilist wettelijk strafbaar. Volgens VVN staat de apparatuur van de politie al jaren		 afgesteld op 0,7 promille waardoor veel bestuurders-in-overtreding niet tegen de lamp lopen.

Een woordvoerder van de politie erkent dat deze marge is ingebouwd om onnauwkeurigheden in de apparatuur te ondervangen. Daarmee wordt voorkomen dat mensen worden vervolgd terwijl later het wettelijk bewijs niet kan worden geleverd."Dat is gebeurd op last van Justitie", zegt hij.


Bij een alcoholcontrole werd 1,45% van de gecontroleerde automobilisten bestraft. Neem aan dat het percentage van 35 in de eerste alinea van het artikel juist is. Als alle automobilisten die teveel hadden gedronken waren bestraft dan zou het percentage niet 1,45 zijn geweest, maar hoger.
4p 15. Bereken dat hogere percentage.

 
In het artikel speelt de onnauwkeurigheid van de apparatuur een belangrijke rol: de metingen geven bijna nooit de werkelijke waarde van het promillage alcohol dat in het bloed aanwezig is. Het verschil tussen het gemeten promillage en het werkelijke promillage noemen we de meetfout.

We gaan er in deze opgave van uit dat de meetfouten normaal verdeeld zijn met een gemiddelde van 0 promille. Afwijkingen naar boven en afwijkingen naar beneden zijn dus even waarschijnlijk. Neem aan dat de standaardafwijking van de meetfouten 0,1 promille is.

Een automo0bilist met 0,48 promille alcohol in het bloed is wettelijk niet strafbaar. Stel dat deze automobilist wordt gecontroleerd. Als de meting meer dan 0,7 promille aangeeft dan wordt deze automobilist (ten onrechte) bestraft.
5p 16. Bereken de kans dat de meetfout zo groot is dat deze automobilist (ten onrechte) wordt bestraft.

 
Toen de grens in de apparatuur op 0,7 promille werd gesteld was de apparatuur nog zo onnauwkeurig dat een ruime marge noodzakelijk was: er zouden anders te veel mensen ten onrechte bestraft worden. Volgens een woordvoerder van 3VO is nauwkeurigheid tegenwoordig geen probleem meer. Kennelijk is de standaardafwijking van de meetfouten bij de huidige apparatuur kleiner geworden.

Neem aan dat de standaardafwijking van de meetfouten tegenwoordig 0,02 promille is. Justitie wil de grens waarop de apparatuur wordt afgesteld zo kiezen dat van de gecontroleerde automobilisten met 0,5 promille alcohol in het bloed slechts 1% (ten onrechte) bestraft wordt.
5p 17. Bereken in twee decimalen nauwkeurig boven welk gemeten promillage automobilisten dan bestraft worden.

 
Opbrengstmodellen
In de economie wordt vaak gebruik gemaakt van wiskundige modellen. Daarin komen formules voor die een theoretisch verband beschrijven tussen economische grootheden.

Een producent verkoopt q eenheden van een product. De totale opbrengst is TO. In de figuur hieronder staat voor vier economische modellen een schets van de grafiek van TO.
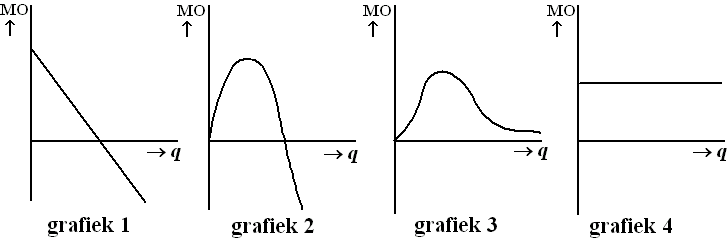
Als we willen weten hoe de totale opbrengst verandert bij een kleine toename van q, dan kijken we naar de marginale opbrengst MO. In de figuur hieronder zie je bij elk van de modellen uit de figuur hierboven de grafiek van de marginale opbrengst, maar ze staan niet in de juiste volgorde.
4p 18. Geef voor elk van de grafieken 1, 2, 3 en 4 uit de tweede figuur aan bij welk model uit de eerste figuur deze hoort. Licht je antwoord toe.

 
We gaan model D uit de bovenste figuur verder bekijken. Stel dat voor het verband tussen q en TO een formule van de volgende vorm geldt:

TO = -0,01 • q3 + b • q2  met b een positief getal.

Bij elke waarde van b kan het maximum van TO worden berekend. De waarde van q waarbij dit maximum optreedt hangt af van b. Deze waarde van q noemen we qmax.
5p 19. Teken een grafiek van het verband tussen qmax en b. Licht je werkwijze toe.

 
OPLOSSINGEN
Het officiλle (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
1. Voor timmeren zijn twee personeelsleden beschikbaar, dus er kan maximaal 80 uur per week getimmerd worden.
Dat is 80 • 60 = 4800 minuten.
x poppenhuizen kost 60x minuten, en y treinen kost 40y minuten. Samen is dat  60x + 40y
De voorwaarde wordt dus  60x + 40y ≤ 4800.  Delen door 20 geeft  3x + 2y ≤ 240
2. Aan x poppenhuizen wordt 24x minuten gezaagd en 60x minuten getimmerd en 40x minuten geverfd.
Samen is dat 124x minuten werk.
Aan y treinen wordt 15y minuten gezaagd en 40y minuten getimmerd en 10y minuten geverfd.
Samen is dat 65y minuten werk
De personeelsleden kosten 30 euro per uur, dat is 0,5 euro per minuut.
De totale kosten aan personeelsleden zijn dan  0,5 • 124x + 0,5 • 65y = 62x + 32,5y  euro.
De materiaalkosten voor x poppenhuizen en y treinen zijn 17x + 17y
De totale kosten worden dan  TK = 62x + 32,5y + 17x + 17y = 79x + 49,5y  euro.

De opbrengst van x poppenhuizen en y treinen is 97x + 58,50y

Winst = Opbrengst - Kosten = (97x + 58,50y) - (79x + 49,5y) = 97x + 58,5y - 79x - 49,5y = 18x + 9y
3. 1e opl. Het toegestane gebied heeft vier hoekpunten. Drie van de vier zijn zo af te lezen:  (0,0) en (60,0) en (0,120)
Het vierde hoekpunt is het snijpunt van de timmer-grenslijn en de verf-grenslijn.
De vergelijkingen daarvan zijn   3x + 2y = 240  en  4x + y = 240
Vermenigvuldig de tweede vergelijking met 2:  8x + 2y = 480
Trek de eerste vergelijking van deze nieuwe vergelijking af:  5x = 240  ofwel  x = 48
Invullen in bijv. de verf-vergelijking geeft  4 • 48 + y = 240  dus  y = 48
Het vierde hoekpunt is dus (48,48)

Bereken de winst in alle vier de hoekpunten:
(0,0) geeft W = 0
(60,0) geeft W = 18 • 60 + 9 • 0 = 1080
(0,120) geeft  W = 18 • 0 + 9 • 120 = 1080
(48,48) geeft  W = 18 • 48 + 9 • 48 = 1296

 De grootste winst is te behalen in het punt (48,48) en bedraagt € 1296,-
2e opl. Teken een paar iso-winstlijnen. Bijv.:
W = 360 is de lijn 18x + 9y = 360  en die gaat door (0,40) en (20,0)
W = 720 is de lijn  18x + 9y = 720 en die gaat door  (0,80) en (40,0)
enz.

Daaraan is te zien dat de winst groter wordt naarmate de isolijnen naar rechts en omhoog schuiven.
De maximale winst zal gehaald worden door de isolijn te kiezen die zo ver mogelijk naar rechts en omhoog is geschoven (evenwijdig aan de al getekende isolijnen) Dat is de isolijn die door het snijpunt van de verf- en de timmerlijnen gaat.
De berekening van dat snijpunt staat hierboven bij de 1e oplossing. (48,38) invullen in W geeft weer € 1296,-
4. Vergelijkingen II, IV en V geven als toegestaan gebied een driehoek met hoekpunten (0,0) en (0,120) en (80,0)
De lijnen bij beide nieuwe vergelijkingen moeten daarbuiten vallen.
Je kunt daar het handigst voor zorgen door naar de snijpunten met de assen te kijken:

8x + 5y = 800 - 20d
Snijpunt met de x-as:  y = 0  dus  8x = 800 - 20d ofwel  x = 100 - 2,5d
Dat moet buiten de driehoek vallen, dus moet x > 80, dus  100 - 2,5d > 80  dus  2,5d < 20  dus  d < 8
Snijpunt met de y-as:  x = 0 dus  5y = 800 - 20d ofwel  y = 160 - 4d
Dat moet buiten de driehoek vallen, dus moet  160 - 4d > 120  dus  4d < 40  dus  d < 10

4x + y  = 240 + 6d
Snijpunt met de x-as:  y = 0  dus  4x = 240 + 6d  ofwel  x = 60 + 1,5d
Dat moet buiten de driehoek vallen, dus moet x > 80 dus  60 + 1,5d > 80 dus 1,5d > 20 dus  d > 13,333...
Snijpunt met de y-as:  x = 0 dus y = 240 + 6d
Dat moet buiten de driehoek vallen, dus moet  240 + 6d > 120  dus  6d > -120  dus  d > -20

 d moet aan alle vier de voorwaarden voldoen, en dat kan niet: d kan niet groter dan 13,3333.. zijn en kleiner dan 8.
Het is dus niet mogelijk.

5. 10 uit de 80 kiezen kan op  80 nCr 10 = 1,64 • 1012 manieren.
6. 1e opl. Je hebt er 10 aangekruist, dus nu zijn er 10 Goed en 70 Fout.

0 goed
De kans op allemaal fout is dan  (70/80)•(69/79)•(68/78)• ... • (49/59)  (hier staan 22 breuken)
Daar komt uit  ongeveer  0,031

2 goed
Een mogelijke volgorde is  GGFFFFFFFFFFFFF....
De kans daarop is  (10/80) • (9/79) • (70/78) • (69/77) •...(51/59) dat is ongeveer 0,001164....
Er zijn  22 nCr 2 zulke volgorden. Dat zijn er dus  231.
De totale kans wordt daarmee  231 • 0,001164... = 0,26892...

 
2e opl. Willekeurig 22 getallen uit de 80 kiezen kan op  80 nCr 22 = 2,70 • 1019 manieren.

0 goed.
22 foute getallen uit de 70 kiezen kan op  70 nCr 22 = 8,58 • 1017 manieren.
De kans dat je 22 foute getallen kiest is dus   (8,58 • 1017)  /  (2,70 • 1019) = 0,031...

2 goed
20 foute getallen uit 70 kan op  70 nCr 20 =  1,62 • 1017 manieren
2 goede uit 10 kiezen kan op  10 nCr 2 = 45 manieren.
Samen geeft dat 45 • 1,62•1017 = 7,28 • 1018 manieren
De kans dat je 20 foute getallen kiest is dus   (8,58 • 1017)  /  (7,28 • 1018) = 0,26892....
7. P(Geldprijs) = 0,054 + 0,395 • 0,054 + 0,395 • 0,395 • 0,054 + .....
Dat zijn de eerste 10 termen van een meetkundige reeks met reden 0,395 en beginwaarde 0,054.
De som daarvan is  Sn = b • (1 - rn) / (1 - r) in dit geval  0,054 • (1 - 0,39510) / (1 - 0,395) = 0,08924....
8. Het minimum aantal getallen vinden we door van elke klasse de ondergrens te nemen.
Dat geeft 260 • 2 + 270 • 1 + 280 • 4 + ... + 350 • 2 = 24400 getallen. En omdat er per trekking 22 getallen worden getrokken zou dat overeenkomen met  24400 / 22  is ongeveer 1110 trekkingen.

Het maximum aantal getallen vinden we door van elke klasse de bovengrens te nemen.
Dat geeft  269 • 2 + 279 • 1 + 289 • 4 + ... + 359 • 2 = 25120 getallen.
Dat komt overeen met  25120 / 22 is ongeveer 1141 trekkingen

1126 trekkingen zou dus goed kunnen wat betreft de gegevens uit deze tabel.
9. Het aantal uilen is met een factor 178/20 = 8,9 toegenomen in een periode van 12 jaar.
De groeifactor per jaar is dan  8,91/12 = 1,19981...  en dat is ongeveer 20% per jaar.
10. t = 0 en 178 uilen geeft  178 = a - b • 0,60 dus  178 = a - b
t = 2 en 205 uilen geeft  205 = a - b • 0,62 dus  205 = a - 0,36b
Uit beide vergelijkingen samen moeten a en b opgelost worden.
De eerste geeft  a = b + 178 en dat kun je invullen in de tweede:  205 = b + 178 - 0,36b
Dus  205 - 178 = b - 0,36b  ⇒  27 = 0,64b ⇒   b = 27/0,64 = 42,1875
Invullen in de eerste vergelijking geeft a = b + 178 = 42,1875 + 178 = 220,1875
Conclusie:  a = 220,19  en  b = 42,19 
11.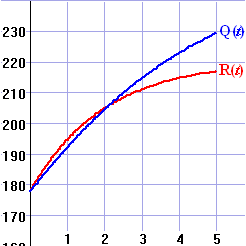
12. Q(t) = 250 • (1 + 0,4045•0,74t)-1 en dat is met de kettingregel te differentiλren:
13. De plot van de afgeleide ziet er zo uit: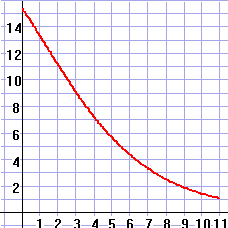



De afgeleide is steeds positief dus de functie is stijgend.
De afgeleide is steeds dalend, dus de functie is afnemend stijgend.
14. Als je in de formule voor Q(t) voor t een groot getal invult, dan nadert de factor 0,74t naar nul, dus gaat de noemer van Q(t) naar 1 en dus gaat Q(t) naar 250.
De gezochte evenwichtswaarde is dus 250.
Bij evenwicht geldt  Nt+1 = Nt = 250
De recursievergelijking wordt dan  250 = c • 250 • (1 - 250/d) + 250
Dat geeft  c • 250 • (1 - 250/d) = 0
Omdat c niet nul kan zijn (dat geeft recursievergelijking Nt+1 = Nt) moet gelden dat  1 - 250/d = 0
Dat is zo als 250/d = 1 ofwel  d = 250.
15. Van de automobilisten die teveel gedronken hebben wordt 100 - 35 = 65% wel bestraft.
Deze 65% is kennelijk 1,45% van alle automobilisten.
65 % van "teveel gedronken"  =  1,45% van "totaal"
1% van "teveel gedronken" = 1,45/65  % van "totaal"
100% van "Teveel gedronken" = 100 • (1,45/65) = 2,23 %  van "totaal".
Dus dat hogere percentage zou 2,23% zijn.
16. Dan moet de meetfout meer dan 0,22 zijn.
NORMALCDF(0.22 , 1E99 , 0 , 0.1) = 0,01390...
17. Noem de grens X.
Een percentage van 1% betekent dat  NORMALCDF(X , 1E99 , 0 , 0.02) gelijk is aan 0,01
Voer in Y1 = NORMALCDF(X, 1E99 , 0 , 0.02)  en Y2 = 0,01
INTERSECT levert  X = 0,0465...
De meetfout mag dus 0,0465 zijn, dat betekent dat de grens bij  0,5 + 0,0465 = 0,55 (afgerond) promille komt te liggen.
18. MO is de helling van TO.
model A heeft constante positieve helling en moet dus wel bij grafiek 4 horen.
model C heeft overal positieve helling, maar niet constant. Daar moet dus grafiek 3 bij horen.
modellen B en D hebben beiden helling eerst positief en daarna negatief.
Een verschil is dat B in het begin positieve helling heeft, en C helling ongeveer nul.
Daarom hoort bij B grafiek 1 en bij C grafiek 2.
Conclusie:  A - 4 ,  B - 1 , C - 3 , D - 2
19. Voor het maximum geldt  TO' = 0  dus  -0,03 • q2 + 2b • q = 0  dus  q • (-0,03q + 2b) = 0
Dat heeft als oplossing behalve q = 0  (minimale opbrengst) ook  -0,03q + 2b= 0
Dat geeft  2b = 0,03q  dus  q = 2b/0,03
Dat is een rechte lijn door  (0,0) en (3,200) en (6,400) en ...... (q op de y-as, b op de x-as)