Nieuwe pagina 1

VWO WISKUNDE A1, 2003 - I

Levensduur van koffiezetapparaten

Enkele jaren geleden is onderzocht hoe lang nieuw aangeschafte koffiezetapparaten meegaan. Op basis daarvan is een kansmodel gemaakt zoals weergegeven in de figuur hieronder. Hierin is bijvoorbeeld te zien dat alle apparaten een half jaar na aanschaf nog in gebruik zijn. Ook is te zien dat voor een apparaat van 1,5 jaar oud de kans 0,97 is dat het een jaar later nog steeds in gebruik is, en dus de kans 0,03 dat het in dat jaar wordt afgedankt.

fig. 1

We passen dit model toe op een groep van 1500 nieuwe koffiezetapparaten. De levensduur van een apparaat is de tijdsduur tussen het aanschaffen en het afdanken van het apparaat. Uit de gegevens in de bovenstaande figuur volgt dat 187 van deze 1500 koffiezetapparaten een levensduur hebben tussen 2,5 en 3,5 jaar.

Laat met een berekening zien dat dit klopt.

Het bovengenoemde getal 187 vind je terug in de volgende tabel. De andere aantallen in deze tabel zijn op overeenkomstige wijze berekend.

levensduur in jaren	aantal koffiezetapparaten
0,5 - 1,5 1,5 - 2,5 2,5 - 3,5 3,5 - 4,5 4,5 - 5,5 5,5 - 6,5 6,5 - 7,5 7,5 - 8,5 > 8,5	15 45 187 313 376 305 163 81 15

Verwerk de gegevens van deze tabel op normaal waarschijnlijkheidspapier en toon daarmee aan dat de levensduur bij benadering normaal verdeeld is met een gemiddelde van 5,0 jaar en een standaardafwijking van 1,6 jaar.

We nemen voor de rest van deze opgave aan dat de levensduur van koffiezetapparaten normaal verdeeld is met een gemiddelde van 5,0 jaar en een standaardafwijking van 1,6 jaar.

Iemand heeft 9 jaar geleden zijn eerste koffiezetapparaat gekocht en nu, 9 jaar later, is net zijn derde koffiezetapparaat kapot gegaan. Hij gaat naar de winkel en moppert tegen de verkoper dat dit toch wel heel uitzonderlijk is.
De klant redeneert als volgt: "Drie koffiezetapparaten in 9 jaar, dat is drie jaar per apparaat. Je zou verwachten dat zo'n apparaat wel langer dan 3 jaar meegaat. De kans dat dit drie keer achter elkaar niet het geval is, is wel heel erg klein"

Bereken de kans dat drie willekeurig gekozen koffiezetapparaten elk een levensduur van ten hoogste drie jaar hebben.

We gaan nog even terug naar het onderzoek uit het begin van de opgave.Voor dit onderzoek heeft men niet een aantal koffiezetapparaten gedurende hun hele levensduur gevolgd. In plaats daarvan heeft men begin januari 1997 een enquête uitgevoerd onder 4000 huishoudens. Deze enquête heeft men precies een half jaar later opnieuw uitgevoerd bij dezelfde 4000 huishoudens. Beide keren werd gevraagd of men een koffiezetapparaat gebruikte en zo ja, in welk kalenderjaar het was aangeschaft.
Op basis van de zo verkregen gegevens hebben de onderzoekers het model van figuur 1 opgesteld. daarbij gingen ze ervan uit dat koffiezetapparaten uit verschillende jaren gelijkwaardig zijn wat de levensduur betreft. Bovendien gingen ze ervan uit dat de koffiezetapparaten uit elk kalenderjaar gelijkmatig gespreid over dat jaar zijn aangeschaft, en dus aan het eind van het jaar van aanschaf gemiddelde een half jaar oud zijn.

Begin januari 1997 gebruikten 506 van de onderzochte huishoudens een koffiezetapparaat dat in 1993 was aangeschaft. Begin januari 1998, een jaar later dus, bleek dat 125 van deze apparaten inmiddels waren afgedankt.

Welke van de kansen uit figuur 1 kan uit deze gegevens worden afgeleid? Licht je antwoord toe met een berekening van de betreffende kans.

De Nederlandse bevolking

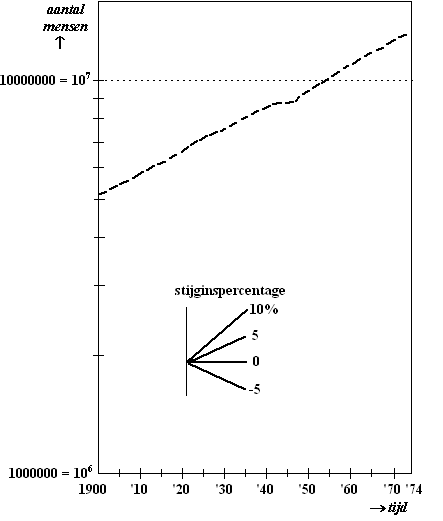
In de figuur hieronder is de groei van de Nederlandse bevolking tussen 1900 en 1974 weergegeven. Zo kun je aflezen dat Nederland in 1900 ruim 5 miljoen inwoners telde. Ook zie je in de figuur een "inzetje" waarin informatie staat over het stijgingspercentage van grafieken bij een logaritmische schaalverdeling.

De bevolking groeide in de beschreven periode bij benadering exponentieel.

Tussen 1 januari 1900 en 1 januari 1974 is de Nederlandse bevolking van 5 miljoen naar 13,4 miljoen mensen gegroeid. Hieruit kunnen we de volgende formule afleiden:

N = 5 • 1,142^t

In deze formule is N het aantal inwoners van Nederland in miljoenen en t de tijd in tientallen jaren met t = 0 op 1 januari 1900.

Toon dat deze formule klopt door de formule af te leiden uit de aantallen van 1900 en 1974.

De grafiek van N vertoont een knikje bij het jaar 1945. Volgens een demograaf die deze grafiek in een artikel gebruikt, betekent deze knik dat er in 1945 ruim 80000 inwoners minder waren dan er volgens bovenstaande formule voor N zouden zijn.

Leg uit hoe de demograaf dit getal gevonden kan hebben. Maak daarbij gebruik van de grafiek hierboven en de formule voor N.

Neem voor de volgende vraag eens aan dat het aantal inwoners van Nederland zich ook na 1974 zou hebben ontwikkeld volgens de formule voor N.

Bereken in welk jaar het aantal van 18 miljoen mensen dan zou worden bereikt.

Met behulp van het inzetje in de figuur kun je groeipercentages aflezen.
Voor de Nederlandse bevolking kun je aflezen dat het groeipercentage tussen 5% en 10% lag. Aan het inzetje is echter niet te zien wat men precies bedoelt. Het zou hier kunnen gaan om:
A) een groeipercentage per jaar
B) een groeipercentage per 5 jaar
C) een groeipercentage per 10 jaar of
D) een groeipercentage per 15 jaar.

Geef met behulp van een berekening aan welke mogelijkheid van de hierboven genoemde mogelijkheden A, B, C of D bedoeld wordt.

Reislust

Reislust is een reisorganisatie die klassieke reizen organiseert. Bij een grote deelname geeft Reislust doorgaans aantrekkelijke kortingen.

In 2002 organiseerde Reislust een reis naar Griekenland. Reislust deed geïnteresseerden een aanbod waarbij men uitging van een basisprijs van 2000 euro per persoon. Deze basisprijs werd verlaagd met 10 euro per deelnemer. Als er bijvoorbeeld 12 personen mee zouden gaan, dan zou men per persoon 2000 - 12 • 10 = 1880 euro betalen.

Na enige tijd bleek dat zich 25 personen hadden opgegeven. Op het laatste moment meldde zich echter nog één persoon meer aan.

Bereken hoeveel Reislust door deze extra aanmelding in totaal meer ontving dan bij een deelname van 25 personen.

Het aantal personen dat meedoet aan een reis noemen we n.

10.

Stel een formule op waarbij je de totale opbrengst van Reislust uitdrukt in n.

Omdat de belangstelling in 2002 toch wat tegenviel overweegt Reislust voor 2003 een ander aanbod. Dit aanbod betreft een reis voor maximaal 53 personen, eveneens naar Griekenland. Ook nu neemt men het basisbedrag van 2000 euro per persoon als uitgangspunt. Vervolgens zorgt elke deelnemer voor een vermindering van het basisbedrag: de eerste deelnemer levert een vermindering van 1 euro op, de tweede deelnemer een vermindering van 2 euro, de derde deelnemer een vermindering van 3 euro, enzovoort. Elke vermindering geldt telkens voor alle deelnemers. Bij een deelname van bijvoorbeeld 5 personen moet elke deelnemer 2000 - (1 + 2 + 3 + 4 + 5) = 1985 euro betalen. Dit aanbod is voor deelnemers pas aantrekkelijk bij grote deelname. Het is zelfs zo dat de prijs per persoon kan zakken tot minder dan 1000 euro.

11.

Onderzoek hoeveel deelnemers zich tenminste moeten opgeven om ervoor te zorgen dat de te betalen prijs op minder dan 1000 euro, per persoon uit zal komen.

Wanneer de reis van 2003 is volgeboekt en er dus 53 deelnemers zijn, wordt de prijs per persoon 569 euro. Dat zou Reislust dan in totaal 53 • 569 = 30157 euro opleveren. Je kunt eenvoudig nagaan dat dit bedrag niet het maximale totale bedrag voor Reislust is, door uit te rekenen dat Reislust bij een deelname van 52 personen een grotere opbrengst heeft.

12.

Bereken hoeveel Reislust in totaal meer ontvangt bij 52 deelnemers.

Reislust berekent dat de totale opbrengst bij het aanbod voor 2003 maximaal is bij 36 deelnemers. De leiding van de reisorganisatie vindt dit aantal te weinig en besluit daarom het aanbod te wijzigen. Uiteindelijk ziet dit er als volgt uit.
Het basisbedrag wordt verlaagd tot 1950 euro. Ook nu zorgt elke deelnemer voor een vermindering van dit basisbedrag: de n de deelnemer levert niet een vermindering van n euro, maar van 0,5n euro op. Elke vermindering geldt weer voor alle deelnemers. Met deze gegevens kunnen we een formule opstellen voor het bedrag T(n) dat Reislust in totaal ontvangt bij een deelname van n personen:

T(n) = n • (1950 - 0,25 • n • (n + 1))

13.

Onderzoek bij welk aantal deelnemers T(n) maximaal is.

Strike it rich

Bij het Engelse televisiespelletje Strike it rich speelt een deelnemer in de finale tien rondes. Bij elke ronde krijgt de deelnemer drie beeldschermen voor zich, waar nog niets op te zien is. De deelnemer moet willekeurig één van deze beeldschermen kiezen. Nadat hij een scherm heeft aangewezen worden alle schermen zichtbaar. Op één van de drie beeldschermen komt "Ga door" te staan, op een ander beeldscherm "Hot Spot" en op het derde beeldscherm "Vraag". Voor alle duidelijkheid: deze woorden worden op aselecte wijze op de beeldschermen geplaatst voordat de deelnemer kiest maar worden pas na zijn keuze zichtbaar voor hem.

Het is mogelijk dat een deelnemer in de tien rondes precies één keer een beeldscherm met Vraag erop aanwijst.

14.

Bereken de kans dat dit het geval is. Geef je antwoord in vier decimalen nauwkeurig.

De deelnemer kan bij elke ronde een strafpunt krijgen. Daarvoor gelden de volgende regels.
Wanneer er op het aangewezen scherm Ga door verschijnt gaat de deelnemer zonder strafpunt door naar de volgende ronde.
Wanneer op het aangewezen scherm Hot Spot verschijnt krijgt de deelnemer een strafpunt en gaat door naar de volgende ronde.
Wanneer er op het aangewezen scherm Vraag verschijnt krijgt de deelnemer een vraag gesteld die hij met Ja of Nee moet beantwoorden. Wanneer het antwoord fout is krijgt hij een strafpunt en gaat door naar de volgende ronde. Wanneer het antwoord goed is gaat hij zonder strafpunt door naar de volgende ronde.

Uit het bovenstaande volgt dat voor een deelnemer die alle vragen foutloos beantwoordt bij iedere ronde de kans op een strafpunt gelijk is aan ¹/₃.
Maar voor een deelnemer die de vragen puur op de gok beantwoordt is bij iedere ronde de kans op en strafpunt gelijk aan ¹/₂.

15.

Toon de juistheid van deze laatste kans met een berekening aan.

16.

Bereken voor deze gokkende deelnemer ook de kans dat hij in tien rondes hoogstens twee strafpunten krijgt. Geef het antwoord in vier decimalen nauwkeurig.

Vóór het begin van het spel moet de deelnemer kiezen of hij voor maximaal 2, maximaal 3 of maximaal 4 strafpunten speelt. Alle strafpunten die de deelnemer gedurende de tien rondes oploopt worden opgeteld. Als hij na tien rondes niet meer dan het gekozen aantal strafpunten heeft, krijgt hij een prijs, zoals vermeld inde volgende tabel (£ betekent Britse pond):

maximum aantal strafpunten waarvoor de deelnemer speelt	prijs als het totaal aantal strafpunten niet boven het gekozen maximum aantal strafpunten uitkomt
2	£ 10000
3	£ 7000
4	£ 5000

Als een deelnemer bijvoorbeeld voor maximaal 3 strafpunten heeft gekozen en hij heeft na tien rondes 3 of minder strafpunten dan krijgt hij de geldprijs van £ 7000. Heeft hij 4 of meer strafpunten dan krijgt hij in dat geval niets.

Voor een deelnemer die alle vragen op de gok beantwoordt is de verwachtingswaarde van de geldprijs zo hoog mogelijk wanneer hij voor maximaal 4 strafpunten speelt. We vragen ons nu af hoe dat zit met een deelnemer die alle vragen foutloos beantwoordt.

17.

Onderzoek voor welk maximum aantal strafpunten deze deelnemer moet spelen om te zorgen dat de verwachtingswaarde van de geldprijs zo hoog mogelijk is.

Sportprestaties.

In de atletiek kent men verschillende onderdelen. De ene atleet is goed in hardlopen, de andere atleet in hoogspringen of speerwerpen. Iemand die de 100 meter binnen de 11 seconden loopt is een goede sprinter, terwijl iemand die met een polsstok hoger springt dan 5 meter een goede polsstokhoogspringer is. Men kan zich afvragen wie van de twee de betere atleet is. Om prestaties bij verschillende atletiekonderdelen te kunnen vergelijken hanteert de Koninklijke Nederlandse Atletiek Unie (KNAU) een puntensysteem. Met dit systeem worden sportprestaties omgerekend tot een aantal punten met behulp van verschillende formules. Vanzelfsprekend hoort bij een betere prestatie een groter aantal punten. Zie de volgende tabel.

In de tabel lezen we af dat voor hardlopen het behaalde aantal punten P wordt berekend met de formule P = ^a/_t - b. Hierbij is t de tijd in seconden die de atleet nodig heeft om de afstand te lopen. De getallen a en b worden afgelezen in de betreffende kolommen voor mannen of vrouwen.
Bijvoorbeeld bij 100 meter hardlopen voor mannen lezen we af dat a = 29550 en voor vrouwen dat a = 30672

Een man en een vrouw lopen allebei de 3000 meter in 8 minuten en 25 seconden.

18.

Bereken hoeveel punten de vrouw meer heeft behaald dan de man.

Als een man de 100 meter in 10,70 seconden loopt, dan heeft hij daarmee 880,2 punten behaald.

19.

Bereken hoeveel seconden, in twee decimalen, een man over de 400 meter moet doen om ook 880,2 punten te behalen.

Voor de spring- en werpnummers wordt de formule P = a√r - b gebruikt. Hierin is r de gesprongen hoogte of afstand in meters of de geworpen afstand in meters. De getallen a en b staan weer in de tabel in de kolommen ernaast. Deze formule is alleen maar zinvol als er een niet te kleine afstand wordt gehaald. Bij zeer kleine afstanden kan het behaalde aantal punten zelfs negatief zijn.

20.

Bereken hoeveel meter een vrouw de discus moet werpen om geen negatief aantal punten te halen. Geef je antwoord in twee decimalen nauwkeurig.

De International Association of Athletics Federations (IAAF) kent ook een puntensysteem. Voor het berekenen van de punten gebruikt de IAAF andere formules dan de KNAU. Bij het speerwerpen voor mannen ziet de IAAF-formule er als volgt uit: P = 10,14 • (r - 7)^1,08.
Wanneer we de formule van speerwerpen voor mannen van de KNAU met die van de IAAF vergelijken, dan blijkt dat voor sommige geworpen afstanden r de formule van de KNAU meer punten oplevert dan de formule van de IAAF.

21.

Onderzoek voor welke waarden van r dat het geval is.

Bij het verspringen voor mannen gebruikt de IAAF de formule:
P = 0,14354 • (100 • (r - 2,2))^1,4. Deze formule kan ook in de IAAF-werpnummer-vorm geschreven worden. In dat geval ziet de IAAF-verspringformule voor mannen eruit als P = a • (r - 2,2)^1,4 voor een bepaalde waarde van a.

22.

Bereken in twee decimalen nauwkeurig hoe groot de waarde van a in dat geval moet zijn.


OPLOSSINGEN

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

Van 2,5 jaar zijn er nog 1500 • 0,99 • 0,97 = 1440 apparaten
Van 3,5 jaar zijn er nog 1500 • 0,99 • 0,97 • 0,87 = 1253 apparaten
Tussen 2,5 en 3,5 jaar zijn dan 1440 - 1253 =187 apparaten.

levensduur in jaren	rechter klassengrens	aantal koffiezetapparaten	aantal cumulatief	percentage cumulatief
0,5 - 1,5 1,5 - 2,5 2,5 - 3,5 3,5 - 4,5 4,5 - 5,5 5,5 - 6,5 6,5 - 7,5 7,5 - 8,5 > 8,5	1,5 2,5 3,5 4,5 5,5 6,5 7,5 8,5 -	15 45 187 313 376 305 163 81 15	15 60 247 560 936 1241 1404 1485 1500	1 4 16,5 37,3 62,4 82,7 93,6 99 100

De tweede kolom op de x-as en de laatste op de y-as uitzetten op het normaal-waarschijnlijkheidspapier levert een (ongeveer) rechte lijn, en daaruit volgt dat de gegevens normaal verdeeld zijn.
Bij 50% vinden we x = 5,0 en dat is het gemiddelde.
Bij 84% vinden we x = 6,6 en dat is het gemiddelde plus de standaardafwijking, dus de standaardafwijking is 6,6 - 5,0 = 1,6

De kans dat één apparaat een levensduur van hoogstens 3 jaar heeft is:
normalcdf(0 , 3 , 5.0 , 1.6) = 0,1048
De kans dat alle drie de apparaten dat hebben is dan 0,1048³ = 0,00115


4.	Een apparaat dat in 1993 is aangeschaft is begin januari 1997 gemiddeld 3,5 jaar oud begin januari 1998 zouden deze apparaten dus 4,5 jaar oud worden. Van de 506 apparaten waren 381 nog in gebruik, en dat is ³⁸¹/₅₀₆ = 0,75296... De pijl van 3,5 naar 4,5 is daarmee uitgerekend.

5.	De 5 is de beginwaarde in 1900. Stel de groeifactor g en de eindwaarde 13,4 in 1974 (t = 7,4) Dan geldt: 13,4 = 5 • g^7,4 ⇒ g^7,4 = 2,68 ⇒ g = 2,68^(1/7,4) = 1,14249959...

6.	1945 is t = 4,5 en dat geeft N = 5 • 1,142^4,5 = 9,087982... ofwel 9087982 inwoners Aflezen in de grafiek geeft N = 10^6,88 = 7585776 Dat scheelt dus ongeveer 1,5 miljoen mensen.

7.	18 = 5 • 1,142^t ⇒ 1,142^t = 3,6 ⇒ t = ^log(3,6)/_log(1,142) = 9,65 Dat is dus 96,5 jaar later en dat is in 1996

8.	Per 10 jaar is de groeifactor 1,142, en de groei dus ongeveer 14%. 5% per jaar is 1,05¹⁰ = 1,6288 dus 63% per 10 jaar. 10% per jaar is nog meer. 5% per 5 jaar is 1,05² = 1,1025 dus 10% per 10 jaar. 10% per 5 jaar geeft 1,1² = 1,21 dus 21% per 10 jaar. De 14% ligt daar tussen, dus het gaat om een percentage per 5 jaar.

9.	Eerst 25 • (2000 - 25 • 10) = 43750 Nu 26 • (200 - 26 • 10) = 45240 Dat is 1490 euro meer.
10.	n deelnemers geeft een prijs per persoon van 2000 - 10•n Dan is de opbrengst n • (2000 - 10•n)

11.	1 + 2 + ..... + n = 1000 (want er moet 1000 euro van de prijs af) 1,2,3... is een rekenkundige rij en voor de som daarvan geldt: Sn = 0,5•n•(eerste + laatste) Dus 0,5 • n(n + 1) = 1000 ⇒ n(n + 1) = 2000 ⇒ n² + n - 2000 = 0 De ABC-formule geeft (naast een negatieve oplossing) n = 44,224.... Dus vanaf 45 personen wordt de prijs minder dan 1000 euro.

12.	Bij 52 personen is de prijs dan 53 euro meer, dus 622 euro. Dat levert 622 • 52 = 32344 euro op en dat is 2187 euro meer.

13.	invoeren Y1 = X • (1950 - 0,25 • X(X + 1)) bijv. met window [0,100]x[0,80000] Dat levert via calc - maximum op dat X = 50,657.... n = 50 geeft (TABLE) 65625 en n = 51 geeft 65637 Dus bij 51 deelnemers is T_n maximaal.


14.	binompdf(10, ¹/₃ , 1) = 0,0867 of: (¹/₃)¹ • (²/₃)⁹ • 10

15.	P(strafpunt) = P(hot spot) + P(vraag én fout) = P(hot spot) + P(vraag) • P(fout) = ¹/₃ + ¹/₃ • ¹/₂ = ¹/₂

16.	binomcdf(10, 0.5 , 2) = 0,0547

17.	Bij 2 strafpunten is de kans op een prijs binomcdf(10, ²/₃ , 2) = 0,00305 de kans op geen prijs is dus 1 - 0,003048 = 0,996952 De verwachtingswaarde is dan 0 • 0,00695 + 10000 • 0,00305 = 30,48 pond Bij 3 strafpunten is de kans op een prijs binomcdf(10, ²/₃ , 3) = 0,01966 de kans op geen prijs is dus 1 - 0,01966 = 0,98034 De verwachtingswaarde is dan 0 • 0,98034 + 0,01966 • 7000 = 137,63 pond Bij 4 strafpunten is de kans op een prijs binomcdf(10, ²/₃ , 4) = 0,07656 de kans op geen prijs is dus 1 - 0,07656 = 0,92344 De verwachtingswaarde is dan 0 • 0,92344 + 0,07656 • 5000 = 382,82 pond De deelnemer moet dus voor 4 strafpunten spelen.


18.	8 minuten en 25 seconden is 505 seconden P_MAN = ^1077300/₅₀₅ - 1234,9 = 898,37 P_VROUW = ^1197450/₅₀₅ - 1176 = 1195,19 Dat is dus 296,82 punten meer


19.	880,2 = ¹¹¹⁹⁶⁰/_t - 1433,5 ⇒ ¹¹¹⁹⁶⁰/_t = 2313,7 Þ t = ¹¹¹⁹⁶⁰/_2313,7 = 48,39 seconden.


20.	224,8 • √r - 686,5 ≥ 0 ⇒ 224,8 • √r ≥ 686,5 ⇒ √r ≥ 3,0538 ⇒ r ≥ 9,33 De vrouw moet de discus minstens 9,33 meter gooien


21.	PLOT Y1 = 190,2 • ÖX - 711,3 en Y2 = 10,14 • (X - 7)^1,08 Dat geeft de plot hiernaast.(window [0,80] × [0,1000]) INTERSECT levert de snijpunten X = 23,27 en X = 67,38 Tussen 23,27 en 67,38 meter levert de KNAU meer punten dan de IAAF.


22.	P = 0,14354 • (100 • (r - 2,2))^1,4 = 0,14354 • 100^1,4 • (r - 2,2)^1,4 = 0,14354 • 630,957 • (r - 2,2)^1,4 = 90,57 • (r - 2,2)^1,4. Dus a = 90,57