Nieuwe pagina 1

VWO WA1, 2002 - II

Vliegen

In de figuur hieronder zie je voor een aantal achtereenvolgende jaren hoeveel passagiers er op luchthaven Schiphol zijn vertrokken of aangekomen.

Rond 1995 besloot de overheid dat Schiphol mocht uitbreiden. Een voorwaarde hiervoor was dat tot en met 2003 het aantal passagiers per jaar ruim onder de 40 miljoen zou blijven. Met behulp van de gegevens uit de figuur hierboven probeerde men te voorspellen of het haalbaar was om aan deze voorwaarde te voldoen. Men nam aan dat na 1992 het aantal passagiers elk jaar met een vast percentage zou groeien.

Een schatting voor dit percentage baseerde men op de groei in de voorafgaande jaren. Men kan bijvoorbeeld de periode 1983 - 1992 nemen en dan als volgt te werk gaan:

neem het aantal passagiers in het eerste en het laatste jaar van deze periode (dus in 1983 en in 1992);
bereken met deze twee aantallen hoe groot het jaarlijks groeipercentage zou zijn als in de tussenliggende periode het aantal passagiers elk jaar met hetzelfde percentage zou zijn gegroeid.
naam aan dat voor elk jaar na 1992 dit groeipercentage geldt.

Bereken op deze wijze of het aantal passagiers per jaar tot en met 2003 onder de grens van 40 miljoen zal blijven.

Door niet naar de periode 1983 - 1992 te kijken, maar naar een andere periode kan men op een lager jaarlijks groeipercentage uitkomen. Men gebruikte hiervoor niet een periode van 9 jaar, zoals de periode 1983 - 1992, maar een periode van 12 jaar.

Welke periode van 12 jaar moet men in de figuur hierboven nemen om op een zo laag mogelijk jaarlijks groeipercentage uit te komen? Licht je keuze toe.

Bij de hierboven beschreven methode zijn alleen de aantallen in het eerste en laatste jaar van de beschouwde periode van belang. De werkelijke groeipercentages voor elk jaar apart spelen daarbij geen rol.
Een journalist meent dat het beter is om deze afzonderlijke groeipercentages wel te berekenen, en daar het gemiddelde van te nemen. Hij neemt als voorbeeld de periode 1981 - 1989. Hij berekent de jaarlijkse groeipercentages in deze periode (dus van 1982 ten opzichte van 1981 enzovoort). Deze zijn achtereenvolgens: 1,0 ; 0,0 ; 8,2 ; 8,5 ; 2,6 ; 13,6 ; 9,7 ; 4,8.
Het gemiddelde hiervan is ^{(1,0 + 0,0 + 8,2 + 8,5 + 2,6 + 13,6 + 9,7
+ 4,8)}/₈ = 6,05.

De journalist meent nu dat je de ontwikkeling tussen 1981 en 1989 goed kunt beschrijven met de aanname dat vanaf 1982 het aantal passagiers 8 jaar lang met 6,05% is toegenomen. Maar als hij met deze aanname, uitgaande van 9,7 miljoen passagiers in 1981, het aantal passagiers in 1989 berekent komt hij niet precies uit op het werkelijke aantal zoals vermeldt in de figuur.

Bereken hoe groot het verschil is tussen het door de journalist berekende aantal passagiers in 1989 en het werkelijke aantal.

Bij het debat over Schiphol speelt geluidshinder een belangrijke rol. Daarbij is niet alleen het aantal vliegbewegingen (starts en landingen) per dag van belang, maar ook hoe die over het etmaal verdeeld zijn. Iemand heeft uit een rapport daarover de onderstaande figuur gekopieerd:

De getallen bij de verticale as zijn bij het kopiëren onleesbaar geworden. Ze zijn nu met vraagtekens aangegeven.

Beredeneer welke getallen in deze figuur bij de verticale as gestaan kunnen hebben. Kies uit:
0 ; 0.1 ; 0.2 ; 0.3 ; 0.4 of
0; 1 ; 2 ; 3 ; 4 of
0 ; 10 ; 20 ; 30 ; 40.
Licht je antwoord toe.

Keno

In de Verenigde Staten kun je op veelplaatsen het kansspel Keno spelen. De spelregels en de te winnen prijzen zijn niet overal hetzelfde. We kijken in deze opgave naar één bepaalde vorm waarin het spel gespeeld kan worden. Een lot kost 1 dollar. Op het lot staan de getallen 1 tot en met 80. Om mee te spelen moet je 10 van deze getallen aankruisen. Dat kan op verschillende manieren. In de figuur hieronder zie je daar een voorbeeld van.

Bereken hoeveel mogelijkheden er zijn om 10 verschillende getallen op het lot te kiezen.

Bij de trekking worden door een trekmachine willekeurig 22 getallen gekozen uit de getallen 1 tot en met 80. Nu gaat het erom hoeveel van de 10 aangekruiste getallen goed zijn. Dat wil zeggen hoeveel er bij de 22 getallen uit de trekkingsmachine zitten. Dit aantal bepaalt de prijs die je wint. Het prijzenschema ziet er als volgt uit:

aantal getallen goed	prijs
10	$250.000,-
9	$2.500,-
8	$250,-
7	$25,-
6	$7,-
5	gratis lot
4	gratis lot
3	geen prijs
2	geen prijs
1	gratis lot
0	$5,-

Opvallend is dat je bij 0 goed een prijs wint en bij 2 of 3 goed niet. Hiervoor is gekozen omdat bijvoorbeeld de kans dat 2 getallen goed zijn veel groter is dan de kans dat 0 getallen goed zijn.

Bereken de kans dat 0 getallen goed zijn en bereken ook de kans dat 2 getallen goed zijn.

Stel dat je één lot koopt. De kans dat je direct een geldprijs wint is ongeveer 5,4% en de kans op een gratis lot ongeveer 39,5%. De kans dat je met dat gratis lot bij de volgende trekking een geldprijs wint is weer 5,4% en de kans dat je opnieuw een gratis lot wint is weer 39,5%. Enzovoort. Zie het diagram hieronder.

Bereken de kans dat je zo bij een van de eerste tien trekkingen een geldprijs wint.

De maker van een website over dit spel verzamelt al sinds de introductie van dit spel de resultaten van alle trekkingen. Hij houdt ook voortdurend bij hoe vaak elk van de 80 getallen getrokken is in alle trekkingen tot dan toe. Op basis daarvan publiceerde hij op een bepaald moment de tabel hieronder. Uit deze tabel blijkt bijvoorbeeld dat tot dat moment 11 van de 80 getallen ten minste 290 en ten hoogste 299 keer waren getrokken.

aantal keren getrokken	aantal getallen
260-269	2
270-279	1
280-289	4
290-299	11
300-309	21
310-319	21
320-329	15
330-339	3
340-349	0
350-359	2

Deze tabel heeft betrekking op een groot aantal trekkingen van telkens 22 getallen. Met behulp van de gegeven in de tabel kunnen we een schatting maken van dit aantal trekkingen. De maker van de website beweerde dat de tabel betrekking had op 1126 trekkingen.

Onderzoek of deze bewering in overeenstemming kan zijn met de gegevens uit deze tabel.

Nieuwbouw

Als een nieuwbouwwoning wordt opgeleverd vindt doorgaans een inspectie plaats. Daarbij komen vaak nog gebreken aan het licht. Uit de nieuwbouwwoningen die bij de oplevering één of meer gebreken vertoonden werd in het jaar 2000 door de Vereniging Eigen Huis een steekproef van 325 woningen genomen. De resultaten zijn samengevat in de volgende tabel.

aantal bij oplevering geconstateerde gebreken	aantal woningen
1 t/m 5 gebreken	5
6 t/m 10 gebreken	21
11 t/m 20 gebreken	85
21 t/m 30 gebreken	88
31 t/m 40 gebreken	59
41 t/m 50 gebreken	47
51 t/m 60 gebreken	7
61 of meer gebreken	13

Van deze 325 woningen bleek het gemiddeld aantal gebreken per woning 28,6 te zijn.

In plaats van het gemiddelde had men ook als centrummaat de mediaan van het aantal gebreken per woning kunnen nemen.
Neem aan dat het aantal woningen steeds bij benadering gelijkmatig over een klasse verdeeld is, behalve bij de laatste klasse.

Onderzoek of de mediaan groter of kleiner is dan het gemiddelde 28,6

Als een nieuwbouwwoning een of meer gebreken vertoont krijgt de bouwer twee weken de tijd om deze te herstellen. Dat blijkt vaak niet te lukken. Bij het onderzoek waren slechts 94 van de 325 woningen na twee weken geheel in orde. De andere 231 woningen vertoonden nog steeds gebreken. Bij één woning vond men zelfs nog 83 gebreken.
Van de 231 woningen die na twee weken nog steeds gebreken vertoonden staan de gegevens over het aantal gebreken per woning in de cumulatieve frequentiepolygoon van de figuur hieronder. Er is gebruik gemaakt van dezelfde klassenindeling als in de tabel hierboven.

Hieronder staan vier schetsen van boxplots van het aantal gebreken per woning.

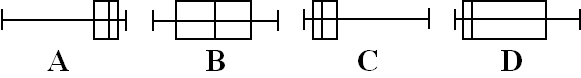10.

Welk van deze boxplots past het beste bij de gegevens van de grafiek hierboven? Licht je antwoord toe, eventueel met behulp van de grafiek.

Omdat na twee weken slechts een klein deel van de 325 woningen in orde is lijkt het net of de bouwers slecht presteren. Maar de 231 woningen die nog niet in orde waren hadden nu gemiddeld ongeveer 8,9 gebreken.
Daaruit volgt dat de bouwers ruim driekwart van alle gebreken hebben verholpen in de herstelperiode van twee weken.

11.

Toon dit met een berekening aan.

Afvallen

Veel mensen doen hun best om hun lichaamsgewicht onder controle te houden. Of je op gewicht blijft, aankomt of afvalt is natuurlijk afhankelijk van wat je per dag eet en drinkt, maar ook van je lichamelijke activiteiten en van je huidige gewicht.
Voor vrouwen met een lengte van 170 cm die normale activiteiten verrichten is in de tabel hieronder het verband weergegeven tussen het lichaamsgewicht en het aantal kilocalorieën (kcal) dat per dag nodig is om op hetzelfde gewicht te blijven.
Wie wil afvallen moet ervoor zorgen minder kilocalorieën binnen te krijgen. Ook daarover geeft de tabel informatie.
In alle organen en spieren wordt energie verbruikt, maar in vetweefsel niet. Dat verklaart waarom de waarden in het onderste gedeelte van de tabel anders verlopen dan in het bovenste gedeelte.

lichaamsgewicht in kg	benodigde aantal kcal per dag voor vrouwen van 170 cm bij normale activiteiten.
lichaamsgewicht in kg	voor behoud huidige gewicht	om 0,5 pond per week af te vallen	om 1 pond per week af te vallen	om 2 pond per week af te vallen
50	1650	1400	1150	650
55	1725	1475	1225	725
60	1800	1550	1300	800
65	1875	1625	1375	875

70	1910	1710	1510	1110
75	1925	1725	1525	1125
80	1940	1740	1540	1140
85	1955	1755	1555	1155
90	1970	1770	1570	1170

Zo lees je af dat een vrouw met een gewicht van 75 kg volgens deze tabel 1925 kcal per dag nodig heeft om op gewicht te blijven. Als ze maar 1525 kcal per dag zou gebruiken dan zou ze 1 pond per week afvallen.

In de tabel zou ook een kolom kunnen staan om 1,5 pond per week af te vallen. Op grond van de regelmaat in de tabel kun je berekenen welke getallen in deze kolom zouden moeten staan.

12.

Bereken de getallen die in deze kolom zouden moeten staan bij een lichaamsgewicht van 70, 75, 80, 85 en 90 kg.

In plaats van deze uitgebreide tabellen is het ook mogelijk formules te geven. Voor vrouwen met een gewicht vanaf 50 kg tot en met 65 kg zijn deze formules dan:

E_behoud = 15 • gewicht + 900
E_{1 pond afvallen} = 15 • gewicht + 400
E_{x pond afvallen} = 15 • gewicht + 900 - 500x

Hierbij geldt:
E_behoud              is het aantal kcal per dag om het huidige gewicht te houden.
E_{1 pond afvallen}    is het aantal kcal per dag om 1 pond per week af te vallen.
E _{x pond afvallen}   is het aantal kcal per dag om x pond per week af te vallen.

Ook voor vrouwen uit de tabel die 70 kg of meer wegen kun je zo drie formules maken.

13.

Maak voor deze groep vrouwen formules voor E_behoud, E_{1 pond afvallen} en E_{x pond
afvallen.}

Wat voor iemand een gezond gewicht is, is onder andere afhankelijk van de lichaamslengte. In de literatuur vind je verschillende methoden om het ideale gewicht te bepalen aan de hand van de lichaamslengte. Volgens een van deze methoden, de Hamwi-methode, is het ideale gewicht voor vrouwen te berekenen met de formule:

ideaal gewicht in kg = 45,4 + 0,89 • (lengte in cm - 152,4)

Een andere veel gebruikte vuistregel zegt dat het maximum voor een gezond lichaamsgewicht kan worden berekend met de formule:

maximumgewicht in kg = 0,0025 • (lengte in cm)²

Het verschil tussen het maximumgewicht volgens de hierboven genoemde vuistregel en het ideale gewicht volgens de Hamwi-methode is niet bij elke lengte hetzelfde.

14.

Bereken de minimale waarde en ook de maximale waarde van dit verschil. Beperk je daarbij tot vrouwen die minstens 155 cm en hoogstens 195 cm lang zijn.

Alcohol

Alle alcoholhoudende dranken bestaan vrijwel uitsluitend uit water en alcohol. De hoeveelheid alcohol in dranken wordt uitgedrukt door een volumepercentage. Dat wil zeggen dat het percentage aangeeft welk deel van het volume uit pure alcohol bestaat. Een liter (= 100 centiliter) bier met een alcoholpercentage van 5% bevat 5 centiliter alcohol en 95 centiliter water. Die 95 centiliter water weegt 950 gram, en die 5 centiliter alcohol weegt 40 gram. Een liter bier weegt dus 990 gram.

De glazen voor verschillende alcoholische dranken zijn zodanig gemaakt dat er 10 gram alcohol in een glas geschonken kan worden. Bier bevat gemiddeld 5% alcohol, jenever bevat 35% alcohol. Een bierglas is dan ook veel groter dan een jeneverglas.

15.

Bereken hoeveel centiliter jenever er in een jeneverglas geschonken kan worden.

Alcohol beïnvloedt de rijvaardigheid. De politie houdt regelmatig alcoholcontroles om automobilisten met een te hoog alcoholpromillage in hun bloed te kunnen bestraffen.

Enkele jaren geleden meende Veilig Verkeer Nederland (tegenwoordig heet deze organisatie 3VO) dat er aan de alcoholcontroles nog wel wat verbeterd zou kunnen worden. Zie het artikel hieronder.

VVN: dronken automobilisten ontspringen te vaak de dans

HUIZEN Veilig Verkeer Nederland (VVN) stoort zich aan de manier waarop de politie omspringt met automobilisten die teveel gedronken hebben. Volgens de organisatie wordt 35 procent van de bestuurders die teveel hebben gedronken niet bestraft omdat de controleapparatuur van de politie te ruim staat afgesteld. ..... Met meer dan 0,5 promille alcohol in het bloed is een automobilist wettelijk strafbaar. Volgens VVN staat de apparatuur van de politie al jaren	afgesteld op 0,7 promille waardoor veel bestuurders-in-overtreding niet tegen de lamp lopen. Een woordvoerder van de politie erkent dat deze marge is ingebouwd om onnauwkeurigheden in de apparatuur te ondervangen. Daarmee wordt voorkomen dat mensen worden vervolgd terwijl later het wettelijk bewijs niet kan worden geleverd."Dat is gebeurd op last van Justitie", zegt hij.

Bij een alcoholcontrole werd 1,45% van de gecontroleerde automobilisten bestraft. Neem aan dat het percentage van 35 in de eerste alinea van het artikel juist is. Als alle automobilisten die teveel hadden gedronken waren bestraft dan zou het percentage niet 1,45 zijn geweest, maar hoger.

16.

Bereken dat hogere percentage.

In het artikel speelt de onnauwkeurigheid van de apparatuur een belangrijke rol: de metingen geven bijna nooit de werkelijke waarde van het promillage alcohol dat in het bloed aanwezig is. Het verschil tussen het gemeten promillage en het werkelijke promillage noemen we de meetfout.

We gaan er in deze opgave van uit dat de meetfouten normaal verdeeld zijn met een gemiddelde van 0 promille. Afwijkingen naar boven en afwijkingen naar beneden zijn dus even waarschijnlijk. Neem aan dat de standaardafwijking van de meetfouten 0,1 promille is.

Een automobilist met 0,48 promille alcohol in het bloed is wettelijk niet strafbaar. Stel dat deze automobilist wordt gecontroleerd. Als de meting meer dan 0,7 promille aangeeft dan wordt deze automobilist (ten onrechte) bestraft.

17.

Bereken de kans dat de meetfout zo groot is dat deze automobilist (ten onrechte) wordt bestraft.

Toen de grens in de apparatuur op 0,7 promille werd gesteld was de apparatuur nog zo onnauwkeurig dat een ruime marge noodzakelijk was: er zouden anders te veel mensen ten onrechte bestraft worden. Volgens een woordvoerder van 3VO is nauwkeurigheid tegenwoordig geen probleem meer. Kennelijk is de standaardafwijking van de meetfouten bij de huidige apparatuur kleiner geworden.

Neem aan dat de standaardafwijking van de meetfouten tegenwoordig 0,02 promille is. Justitie wil de grens waarop de apparatuur wordt afgesteld zo kiezen dat van de gecontroleerde automobilisten met 0,5 promille alcohol in het bloed slechts 1% (ten onrechte) bestraft wordt.

18.

Bereken in twee decimalen nauwkeurig boven welk gemeten promillage automobilisten dan bestraft worden.


OPLOSSINGEN

Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.

1.	In 1983 waren er 9,8 miljoen passagiers en in 1992 18,7 miljoen. Daartussen zit een factor ^18,7/_9,8 = 1,90816.... Dat was in 9 jaar. Per jaar is dat 1,90816...^1/9 = 1,07443.... Van 1992 naar 2003 is 11 jaar. In 2003 zullen er dan 18,7 • 1,07443...¹¹ = 41,1923... miljoen passagiers zijn. Het aantal zal dus niet onder de grens van 40 miljoen blijven.

2.	van 1978 - 1990 geeft een factor ^16,3/_9,2 = 1,77... van 1979 - 1991 geeft een factor ^16,2/_9,8 = 1,65... van 1980 - 1992 geeft een factor ^18,7/_9,5 = 1,96... Dus de periode 1979 - 1991 geeft de kleinste groeifactor.

3.	De journalist vindt voor 1989: 9,7 • 1,065⁸ = 16,1 miljoen passagiers. Het werkelijke aantal was 15,4 miljoen, dus dat scheelt 0,7 miljoen passagiers.

4.	Tussen twee tijdstippen van 2 uur staan steeds 8 staafjes, dus de hele figuur bevat 12•8 = 96 staafjes. Samen zijn die 100%, dus de staafjes hebben een gemiddelde hoogte van ¹⁰⁰/₉₆ is ongeveer 1%. Daarom zal op de verticale as 0 ; 1 ; 2 ; 3 ; 4 hebben gestaan.

5.	10 uit de 80 kiezen kan op 80 nCr 10 = 1,64 • 10¹² manieren.

6.	1^e opl.	Je hebt er 10 aangekruist, dus nu zijn er 10 Goed en 70 Fout. 0 goed De kans op allemaal fout is dan (70/80)•(69/79)•(68/78)• ... • (49/59) (hier staan 22 breuken) Daar komt uit ongeveer 0,031 2 goed Een mogelijke volgorde is GGFFFFFFFFFFFFF.... De kans daarop is (¹⁰/₈₀) • (⁹/₇₉) • (⁷⁰/₇₈) • (⁶⁹/₇₇) •...(⁵¹/₅₉) dat is ongeveer 0,001164.... Er zijn 22 nCr 2 zulke volgorden. Dat zijn er dus 231. De totale kans wordt daarmee 231 • 0,001164... = 0,26892...
	2^e opl.	Willekeurig 22 getallen uit de 80 kiezen kan op 80 nCr 22 = 2,70•10¹⁹ manieren. 0 goed. 22 foute getallen uit de 70 kiezen kan op 70 nCr 22 = 8,58 • 10¹⁷ manieren. De kans dat je 22 foute getallen kiest is dus (8,58 • 10¹⁷) / (2,70 • 10¹⁹) = 0,031... 2 goed 20 foute getallen uit 70 kan op 70 nCr 20 = 1,62•10¹⁷ manieren 2 goede uit 10 kiezen kan op 10 nCr 2 = 45 manieren. Samen geeft dat 45 • 1,62•10¹⁷ = 7,28 • 10¹⁸ manieren De kans dat je 20 foute getallen kiest is dus (8,58 • 10¹⁷) / (7,28 • 10¹⁸) = 0,26892....

7.	P(Geldprijs) = 0,054 + 0,395 • 0,054 + 0,395 • 0,395 • 0,054 + ..... Dat zijn de eerste 10 termen van een meetkundige reeks met reden 0,395 en beginwaarde 0,054. De som daarvan is S_n = b • (1 - rⁿ) / (1 - r) in dit geval 0,054•(1 - 0,395¹⁰) / (1 - 0,395) = 0,08924....

8.	Het minimum aantal getallen vinden we door van elke klasse de ondergrens te nemen. Dat geeft 260 • 2 + 270 • 1 + 280 • 4 + ... + 350 • 2 = 24400 getallen. En omdat er per trekking 22 getallen worden getrokken zou dat overeenkomen met ²⁴⁴⁰⁰/ ₂₂ is ongeveer 1110 trekkingen. Het maximum aantal getallen vinden we door van elke klasse de bovengrens te nemen. Dat geeft 269 • 2 + 279 • 1 + 289 • 4 + ... + 359 • 2 = 25120 getallen. Dat komt overeen met ²⁵¹²⁰ / ₂₂ is ongeveer 1141 trekkingen 1126 trekkingen zou dus goed kunnen wat betreft de gegevens uit deze tabel.

9.	De middelste van 325 is nr. 163. Na de eerste drie klassen hebben we 111 gevallen gehad. Om de 163^ste te krijgen moeten er nog 52 gevallen bij van de vierde klasse van totaal 88. Dat is (⁵²/₈₈)^ste deel van die vierde klasse. De klasse loopt van 21 tm 30. Dat zijn 10 waarden, en ⁵²/₈₈^ste deel daarvan is 5,90. De mediaan zal zijn 25,90 gebreken. Ofwel 25 à 26 gebreken.

10.	In het begin (bij weinig gebreken) neemt het cumulatieve frequentiepolygoon sterk toe, later steeds minder. Dat betekent dat er bij weinig gebreken veel woningen waren, en als het aantal gebreken toeneemt, neemt het aantal woningen af. (Het histogram zal in het begin hoog zijn, en steeds lager worden) Maar als de frequentie hoog is, is de boxplot smal (er is maar een kleine klassebreedte nodig om een kwart van de metingen te hebben) en als de frequentie lager is, is de boxplot breder. De boxplot is dus in het begin smal en wordt steeds breder. Dat is boxplot C.

11.	Eerst waren er 28,6 • 325 = 9295 gebreken. Na twee weken waren er nog 8,9 • 231 = 2056 (afgerond) gebreken. Dat betekent dat 7239 gebreken zijn hersteld, en dat is (7239 / 9295) • 100% = 77,9 % en dat is ruim driekwart.

12.	Per half pond afvallen scheelt 200 kcal. Om de waarden bij 1,5 pond afvallen te krijgen kun je dus bij de waarden van 1,0 pond 200 kcal aftrekken of bij de waarden van 2,0 pond 200 kcal optellen. Dat geeft voor 70, 75, 80, 85 en 90 kg waarden van respectievelijk 1310, 1325, 1340, 1355 en 1370 kcal.

13.	Per 5 kg lichaamsgewicht is de toename in een kolom 15 kcal. Per kg is dat 3 kcal, dus de formules zullen de vorm E = 3 • gewicht + b hebben. Om b te vinden vul je gewoon een waarde in. Neem bijvoorbeeld die bij 70 kg. E_behoud: 1910 = 3 • 70 + b dus b = 1700 en de formule wordt E_behoud = 3 • gewicht + 1700 E_{1pond afvallen}: 1510 = 3 • 70 + b dus b = 1300 en de formule wordt E_{1 pond afvallen} = 3 • gewicht + 1300 De laatste formule zal de vorm E_{x pond afvallen} = 3 • gewicht + b + a • x hebben. In een rij van de tabel zie je dat per pond afvallen 400 kcal scheelt. Daarom zal a uit de formule gelijk zijn aan -400 Invullen van bijv. x = 0, gewicht = 70, kcal = 1910 geeft nu 1910 = 3 • 70 + b - 400 • 0 ofwel b = 1700 Daarmee wordt de formule E_{x pond afvallen}= 3 • gewicht + 1700 - 400x.

14.	Noem de lengte X en het gewicht Y. Voer in de GR de formules Y1 = 45,4 + 0,79•(X - 152,4) en Y2 = 0,0025•X² in. Het gaat om het verschil tussen beiden, Dat kun je in beeld krijgen door Y3 = Y2 - Y1 in te voeren (Y krijg je via VARS - YVARS -Function) Neem WINDOW bijvoorbeeld Xmin = 155 , Xmax = 195 , Ymin = 10 en Ymax = 15. Dat geeft een maximum bij X = 155 van 12,3485 kg (te vinden via TABLE) En dat geeft een minimum bij X = 178 van 11,026 kg (te vinden via CALC - Minimum)

15.	5 cl alcohol weegt 40 gram, dus 1 cl weegt 8 gram. Voor 10 gram alcohol is ¹⁰/₈ = 1,25 cl alcohol nodig. 1,25 cl is 35% van het hele glas. Het hele glas is 100%, en dat is dan (100/35) • 1,25 = 3,5714... cl.

16.	Van de automobilisten die teveel gedronken hebben wordt 100 - 35 = 65% wel bestraft. Deze 65% is kennelijk 1,45% van alle automobilisten. 65 % van "teveel gedronken" = 1,45% van "totaal" 1% van "teveel gedronken" = ^1,45 /₆₅ % van "totaal" 100% van "Teveel gedronken" = 100 • (^1,45/ ₆₅) = 2,23 % van "totaal". Dus dat hogere percentage zou 2,23% zijn.

17.	Dan moet de meetfout meer dan 0,22 zijn. NORMALCDF(0.22 , 1E99 , 0 , 0.1) = 0,01390...

18.	Noem de grens X. Een percentage van 1% betekent dat NORMALCDF(X , 1E99 , 0 , 0.02) gelijk is aan 0,01 Voer in Y1 = NORMALCDF(X, 1E99 , 0 , 0.02) en Y2 = 0,01 INTERSECT levert X = 0,0465... De meetfout mag dus 0,0465 zijn, dat betekent dat de grens bij 0,5 + 0,0465 = 0,55 (afgerond) promille komt te liggen.