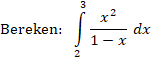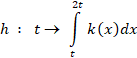| Vraagstuk 5 was alleen bedoeld voor in 1975 afgewezen kandidaten. Zij behoefden vraagstuk 4 niet te maken. | |||
| 1. | Voor elke p ∈ ℝ is de functie fp van ℝ naar ℝ gegeven door: | ||
| x → x3 - px2 + 9x | |||
| a. | Onderzoek de functie f6 en teken de grafiek van f6. | ||
| b. | Bereken de oppervlakte van het vlakdeel dat ingesloten wordt door de grafiek van f6 en de x-as. | ||
| c. | Voor welke p ∈ ℝ heeft elke lijn die evenwijdig is aan de x-as met de grafiek van fp precies één punt gemeen? | ||
| 2. | Voor elke p ∈ ℝ is Gp de grafiek van relatie van ℝ naar ℝ: | ||
| Rp = { (x, y) | x2 + pxy = 2px + 2y}. | |||
| a. | Door welke punten gaan alle grafieken Gp ? | ||
| b. | Voor welke p ∈ ℝ geldt: { (x, y) | y = x} Ì Rp ? | ||
| c. | Bewijs dat de punten van alle grafieken Gp waarin de raaklijn evenwijdig is aan de x-as, op een parabool liggen. | ||
| 3. | De kromme K is ten opzichte van een rechthoekig assenstelsel gegeven door: | ||
| x = 2sint en y = t + 2sint waarin t ∈ [0, 2π] | |||
| a. | Bereken de
coördinaten van de gemeenschappelijke punten van K en de y-as. Bewijs dat K slechts één punt gemeen heeft met de x-as. |
||
| b. | Bereken de
coördinaten van de punten van K waarin de lijn die K raakt
evenwijdig is aan de x-as of aan de y-as. Teken de kromme K |
||
| c. | De
richtingscoëfficiënt van de lijn die K in punt (2sint,
t + 2sint) raakt, noemt men mt. Bereken het bereik van de functie t → mt. |
||
| 4. | Men werpt met twee
zuivere dobbelstenen. De stochast X is de som van de aantallen ogen die met de twee stenen gegooid worden. De stochast Y is het product van deze aantallen. |
||
| a. | Bewijs dat X en Y afhankelijke stochasten zijn. | ||
| b. | Bereken de kans dat de stochast X in 20 worpen precies 5 keer gelijk is aan 7. | ||
| c. | Twee personen A en
B maken de volgende afspraak: A betaalt 3 gulden aan B als de stochast Y gelijk is aan een even getal; A ontvangt 9 gulden van B als de stochast Y gelijk is aan een oneven getal. Bereken de kans dat A na 10 worpen meer geld van B ontvangen geeft dan hij aan B betaald heeft. |
||
| 5. | a. |
|
|
| b. | Gegeven zijn van ℝ naar ℝ de functies: | ||
|
|
|||
| Bewijs dat de grafiek van g verkregen kan worden uit de grafiek van f door een vermenigvuldiging ten opzichte van de oorsprong. | |||
| c. | De functie h van ℝ naar ℝ is gegeven door: | ||
|
|
|||
| waarin k een
functie is die een primitieve heeft met domein
ℝ. Bewijs dat h '(t) = 2k(2t) - k(t) |
|||