HAVO WB, 2019 - I

 

Formule van Wilson.
       

De geluidssnelheid in zeewater kan worden benaderd met de formule van Wilson:

 v = 1449,2  + 4,623T  - 0,0546T2  + 1,391(Z - 35)  + D/60

Hierin is:
- v de geluidssnelheid in m/s;
- T de watertemperatuur in ºC;
- Z het zoutgehalte van het zeewater in promille (‰);
- D de waterdiepte in m.

In enkele gesloten zeeën (zoals de Kaspische Zee en de Dode Zee) wijkt het zoutgehalte sterk af van het zoutgehalte van open zeeën. Zo is het zoutgehalte van de Dode Zee met 337‰ ongeveer 10 keer zo hoog als het zoutgehalte van gewoon zeewater.
De Kaspische Zee is met een gemiddeld zoutgehalte van 12‰ veel minder zout dan gewoon zeewater.
       

3p.

1.

Bereken bij gelijke watertemperatuur (T) en gelijke waterdiepte (D) het verschil tussen de geluidssnelheid in de Dode Zee en in de Kaspische Zee. Geef je eindantwoord in een geheel aantal m/s.
     

 

Bij een bepaalde watertemperatuur zal de geluidssnelheid in zeewater maximaal zijn. Deze watertemperatuur is onafhankelijk van de waterdiepte en het zoutgehalte. Daarom mogen Z en D als constanten worden beschouwd bij het berekenen van deze watertemperatuur.
       

3p.

2.

Bereken algebraïsch de temperatuur in graden Celsius waarbij de geluidssnelheid in zeewater maximaal is. Geef je eindantwoord in één decimaal.
     

 

Vanuit een onderzeeboot kan men door middel van een sonarapparaat afstanden bepalen. Hiervoor zendt de onderzeeboot een geluidssignaal uit. Door een ander object in het water wordt dit signaal teruggekaatst.
Men meet het tijdsverschil tussen het moment van uitzenden van het signaal en het moment waarop het teruggekaatste signaal weer ontvangen wordt.

Een onderzeeboot en een object bevinden zich op 20 meter diepte in zeewater van 10 ºC met een zoutgehalte van 35‰. De onderzeeboot zendt een geluidssignaal uit, dat door het object wordt teruggekaatst; 12,45 seconden nadat het is uitgezonden wordt het teruggekaatste signaal weer opgevangen.
       

3p.

3.

Bereken hoe ver het object van de onderzeeboot verwijderd is. Geef je eindantwoord in honderden meters.
     

 
Ingeklemd.
       

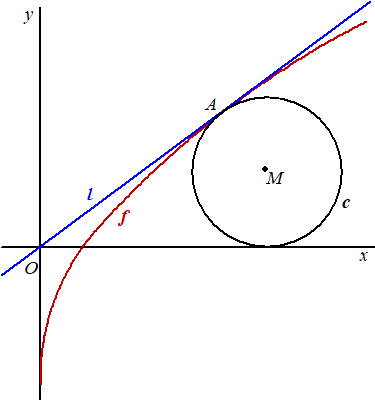
De functie f  is gegeven door   f(x) = -3 + 3√x .

Het punt A(4, 3) ligt op de grafiek van f.

Verder is de lijn l met vergelijking  y = 3/4 • x gegeven.

Lijn l raakt de grafiek van f in A.
       

4p.

4.

 Bewijs dit.
     

 

De cirkel c heeft middelpunt M met  xM  = 5 .

Bovendien raakt lijn l cirkel c in punt A. Zie de figuur.
       

       

5p.

5.

 Bewijs dat c de x-as raakt.
     

 
Twee exponentiële functies.
       

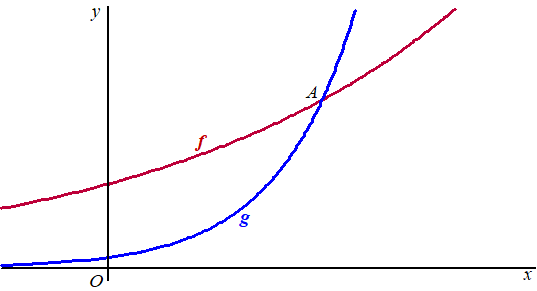
De functies f en g zijn gegeven door:

       
Het punt A is het snijpunt van de grafieken van f en g. Zie de figuur.
       

       

4p.

6.

 Bereken exact de coördinaten van A.
     

 

Bij de grafiek van  f  hoort de formule y = 2½x + 3.

Deze formule kan worden herschreven zodat x wordt uitgedrukt in y.
       

3p.

7.

 Druk x uit in y.
     

 
In of Uit.
       

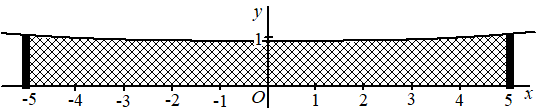
Bij tennis is het net aan de zijkanten hoger dan in het midden. Zie de foto.

De bovenrand van het net hangt aan de zijkanten op een hoogte van 1,07 meter en in het midden op een hoogte van 0,91 meter.
Het net is 10,06 meter breed.

We plaatsen dit net in een assenstelsel met het midden van het net op de
y-as en de onderkant van het net op de x-as. Zie de onderstaande figuur.

 

       

De hoogte y van een willekeurig punt op de bovenrand van het net is te benaderen door een parabool met een formule van de vorm y = px2 + q   met -5,03 ≤ x ≤ 5,03. Hierbij zijn x en y in meters.
       

4p.

8.

Bereken de waarden van p en q die uit de gegevens volgen. Geef p in drie decimalen en q in twee decimalen.
     

 

Bij tennis is het soms moeilijk om te beoordelen of een bal binnen of buiten de lijnen de grond raakt. Vaak wordt met behulp van camera’s vastgesteld waar een bal de grond raakt.

Om een idee te krijgen hoe zo’n systeem werkt, bekijken we een sterk vereenvoudigd tweedimensionaal model met twee camera’s. In onderstaande figuur is een bovenaanzicht van één helft van het rechthoekige speelveld weergegeven. Bovendien zijn in deze figuur enkele maten gegeven. Alle maten zijn in meters.
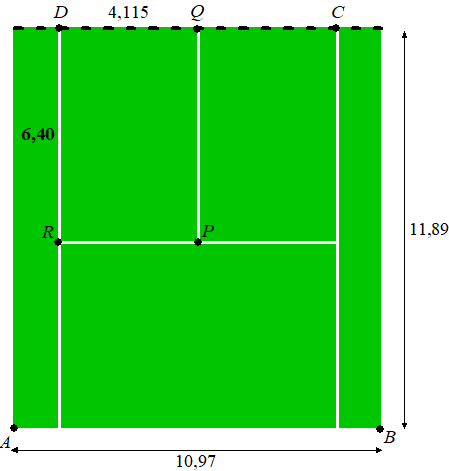
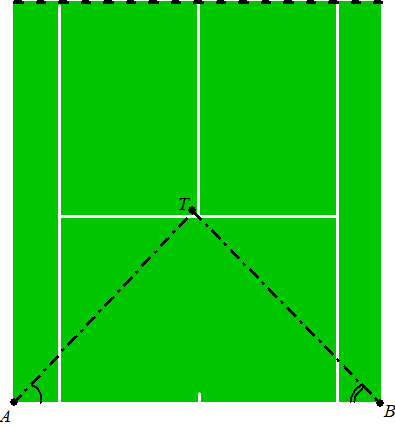
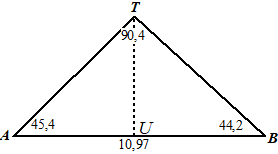
Ook zijn de witte lijnen op het speelveld aangegeven. In het vervolg van deze opgave verwaarlozen we de breedte van deze lijnen. De bal beschouwen we als een punt.
       

       

In deze figuur geldt:
- de stippellijn door CD geeft de plaats van het net aan;
- de lengte van de achterlijn AB is 10,97 m;
- de afstand van de achterlijn tot aan het net is 11,89 m;
-  DQ = 4,115 m en DR = 6,40 m;
-  rechthoek PQDR is het servicevak, waarin de bal volgens de regels van het spel na de eerste slag op de grond moet komen.
       

In de volgende figuur is hetzelfde speelveld als nogmaals weergegeven.
De camera’s zijn boven de punten A en B gemonteerd.
       

       

In deze figuur geldt:
- A is de positie van camera 1 en B is de positie van camera 2;
-

het punt T is de plaats waar de bal na de eerste slag op de grond komt;
-

∠A is de hoek ten opzichte van de achterlijn waaronder camera 1 de bal waarneemt;
-

∠B is de hoek ten opzichte van de achterlijn waaronder camera 2 de bal waarneemt;
-

In de situatie zoals weergeven in de figuur is de bal nog net in het servicevak PQDR op de grond gekomen.
       
We bekijken nu een andere situatie, waarbij ∠A = 45,4° en ∠B = 44,2° .
       

6p.

9.

Onderzoek met behulp van een berekening of in deze situatie de bal in rechthoek PQDR op de grond is gekomen.
     

  
       
Grafiek van een derdegraadsfunctie en een lijn.
       

De functie f is gegeven door f (x) = (1/2x - 2)3 . Zie de figuur.
       

       

De functie g is gegeven door g(x) = x3. De grafiek van f ontstaat uit de grafiek van g door twee transformaties na elkaar toe te passen.
       

3p.

10.

Geef aan welke twee transformaties dit kunnen zijn en in welke volgorde ze moeten worden toegepast.
     

 

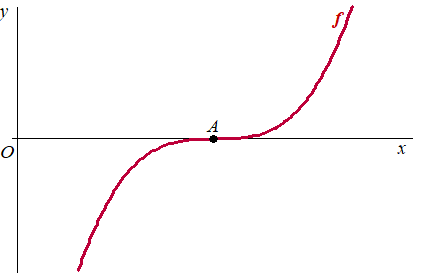
De grafiek van f snijdt de x-as in het punt A. Zie de figuur.

De grafiek van f heeft een horizontale raaklijn in A.
       

5p.

11.

 Bewijs dit.

 
       

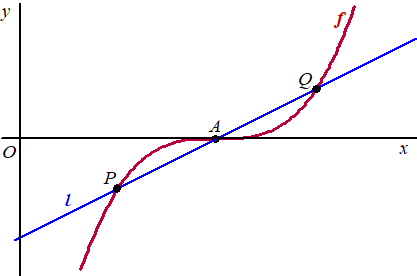
De lijn l met vergelijking   y = 1/2x - 2 snijdt de grafiek van f behalve in punt A ook in de punten P en Q.
Zie onderstaande figuur.
       

       

3p.

12.

 Bereken de lengte van PQ. Geef je eindantwoord in twee decimalen.
     

  
Sinusoïden.
       
Op het domein [0, 2π] is de functie f gegeven door:
       

       

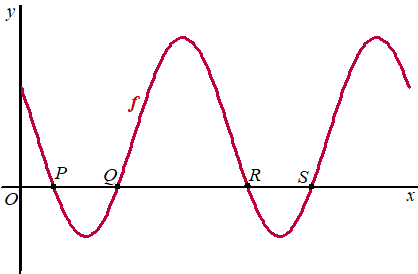
De grafiek van f snijdt de x-as achtereenvolgens in de punten P, Q, R en S. Zie de figuur.
       

       
De afstand PS is a keer zo groot als de afstand QR.
       

5p.

13.

 Bereken de waarde van a
     

 
Op hetzelfde domein  [0, 2π] is functie g gegeven door:

       

De grafiek van g is ook een sinusoïde. Met andere woorden: g heeft een functievoorschrift van de vorm
g(x) = p + q • cos(r (x - s)).
       

5p.

14.

Bereken mogelijke waarden van p, q, r en s. Geef deze waarden zo nodig in drie decimalen.
     

 
Schaal van Richter.
       
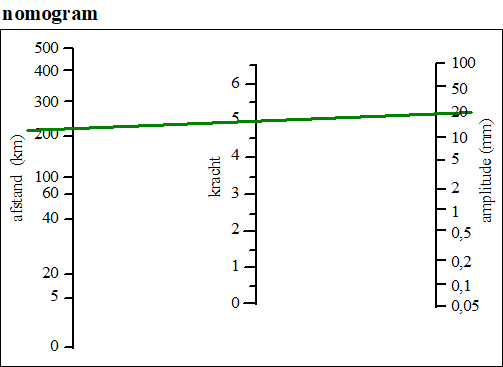
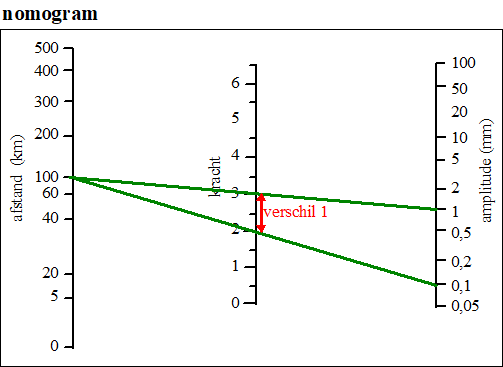
Charles Richter heeft in 1935 een schaal opgesteld die de kracht van een aardbeving in een getal uitdrukt. Dit wordt de schaal van Richter genoemd.

De plaats waar een aardbeving ontstaat heet het epicentrum. Het is mogelijk om op een bepaalde afstand tot het epicentrum de kracht van een aardbeving te bepalen. Hiervoor wordt de grootte van de beweging van de aardkorst in verticale richting gemeten. Deze verticale uitwijking is de zogeheten amplitude.

De kracht van een aardbeving kan bepaald worden met behulp van een nomogram. Hierbij wordt de afstand van de plaats van meting tot het epicentrum als punt op de as ‘afstand’ in het nomogram aangegeven. De gemeten amplitude wordt als punt op de as ‘amplitude’ in het nomogram aangegeven. Het snijpunt van de lijn door deze twee punten met de middelste as (kracht) geeft de kracht van de aardbeving. Zie hieronder.
       

       
In het nomogram zie je bijvoorbeeld dat als op een afstand van ongeveer 220 km vanaf het epicentrum de amplitude 20 mm is, er een aardbeving heeft plaatsgevonden met een kracht van 5 op de schaal van Richter.

Er geldt: als de amplitude van de ene aardbeving tien keer zo groot is als de amplitude van een andere aardbeving, dan is de kracht van de zwaarste beving 1,0 groter dan de kracht van de lichtste beving.
       

4p.

15.

Laat dit zien voor twee aardbevingen waarvan op 100 km van het epicentrum de ene een amplitude van 0,1 mm heeft en de andere een amplitude van 1 mm. Maak hierbij gebruik van het nomogram.
       

Ook met behulp van een formule kan uit de afstand D tot het epicentrum en de amplitude A de kracht op de schaal van Richter berekend worden.
Deze kracht wordt in één decimaal nauwkeurig gegeven.

Voor de kracht op de schaal van Richter geldt:
 


K = log(A) + 1,6 • log(D) - 0,15    voor D ≤ 200      .....(1)

K = log(A) +  3 • log(D) - 3,38      voor D > 200      .....(2)

       

Hierin is K de kracht op de schaal van Richter,  A de amplitude in mm en D de afstand tot het epicentrum in km.

De hoeveelheid schade die een aardbeving aanricht, hangt af van de amplitude. Bij een amplitude van meer dan 1000 mm is er grote kans op schade aan gebouwen. Hoe verder men van het epicentrum verwijderd is, hoe kleiner de amplitude.

Op 12 mei 2008 was er in de regio Sichuan in China een aardbeving met een kracht van 7,9 op de schaal van Richter. Het cirkelvormige gebied rond het epicentrum waar de amplitude minstens 1000 mm bedroeg, werd tot rampgebied uitgeroepen.
       

5p.

16.

Bereken met behulp van formule (2) de oppervlakte van het rampgebied in vierkante kilometers. Geef je eindantwoord in duizendtallen.
     

 

Formule (1) is te schrijven in de vorm:    K = log( p • A • Dq)
       

5p.

17.

 Bereken p en q. Geef je eindantwoorden in één decimaal.
     

 
Loodrecht en Raken.
       

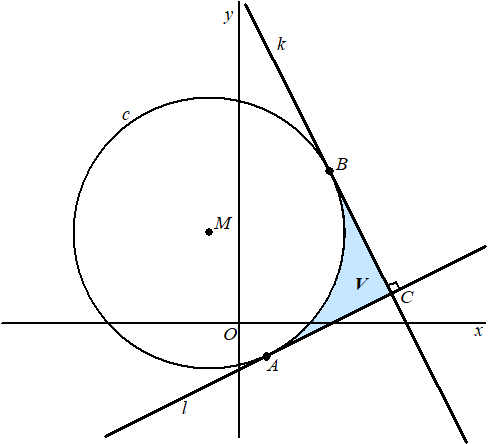
Cirkel c met middelpunt M(-1, 3) raakt lijn l met vergelijking   y = 1/2x - 11/2  in punt A.

Lijn k staat loodrecht op l en raakt c in punt B. Punt C is het snijpunt van k en l.

Lijnstukken AC en BC en cirkelboog AB sluiten het vlak V in. Zie de figuur, waarin vlak V blauw is weergegeven.
       

       

8p.

18.

Bereken algebraïsch de omtrek van V. Geef je eindantwoord in twee decimalen.
     

 

 

 

UITWERKING
   
Het officiële (maar soms beknoptere) correctievoorschrift kun je HIER vinden. Vooral handig voor de onderverdeling van de punten.
   
1. Kies zomaar wat voor T en D want die doen er niet toe, bijvoorbeeld T = 15 en D = 3
Dat geeft   
Dode zee:  v = 1449,2  + 4,623 • 15  - 0,0546 • 152  + 1,391(337 - 35)  + 3/60  =  1926,392
Kaspische Zee:  v = 1449,2  + 4,623 • 15  - 0,0546 • 152  + 1,391(12 - 35)  + 3/60  = 1474,317
Dat scheelt  1926,392 - 1474,317 = 452  m/s
   
2. De geluidssnelheid is maximaal als de afgeleide ervan nul is.
De stukken met D en Z zijn constant, dus daarvan is de afgeleide nul.
Dat geeft:  v ' = 4,623 - 2 • 0,0546T  = 0
0,1092T = 4,623  geeft  T = 42,3ºC
   
3. T = 10, D = 20, Z = 35 
geeft  v = 1449,2  + 4,623 • 10  - 0,0546 • 102  + 1,391(35 - 35)  + 20/60 = 1490,3033...  m/s
in 12,45 seconden wordt dan 12,45 • 1490,3033... = 18554,2765 meter afgelegd.
Maar dat is heen-en-terug, dus de afstand is de helft:  9277,138... ≈ 9300 meter.
   
4. l raakt de grafiek van f op de plaats waar hun hellingen gelijk zijn.
Dus moet gelden f ' = 0,75
f  ' = 3/(2√x)  = 0,75
0,75 • 2√x = 3
√x = 2
x = 4
Dan is  f(x) = -3 + 3√4 = 3
op l is dan   y = 0,75 • 4 = 3
Beiden leveren inderdaad punt A op.
   
5. MA staat loodrecht op l dus AM heeft helling  -4/3
A = (4, 3)  dus voor AM geldt   3 = -4/3 • 4 + b   en dat geeft b =  81/3
MA is de lijn  y = -4/3x + 81/3.
M ligt bij x = 5, dus  y = -4/3 • 5 + 81/3 = 5/3
M = (5, 5/3)  en  A = (4, 3)  dus  AM = √((5 - 4)2 + (5/3 - 3)2) = 5/3
De straal van de cirkel is gelijk aan de y-coördinaat van M dus c raakt de x-as
   
6. 20,5x + 3 = 4x 
20,5x + 3 = (22)x
20,5x + 3 = 22x
0,5x + 3 = 2x
1,5x = 3
x = 2  en y = 42 = 16  dus  A = (2, 16)
   
7.  y = 2½x + 3
2logy = 0,5x + 3
2loy - 3 = 0,5x
x = 2 • 2logy - 6
   
8. y = px2 + q  moet door  (0, 0.91) gaan
Dat geeft  0,91 = 0 • p + q  dus  q = 0,91
Dus  y = px2 + 0,91
Moet ook door  (5.03, 1.07) gaan:   1,07 = p • 5,032 + 0,91
p • 25,3009 = 0,16
p = 0,00632388...≈  0,006
   
9. Het gaat om de volgende driehoek:
 

  ∠T = 180 - 44,2 - 45,4 = 90,4
Sinusregel:  10,97/sin(90,4) = AT/sin(44,2)  geeft  10,97.. = AT/0,697...  dus  AT = 7,648...
U is de projectie van T op AB.

in driehoek AUT:   sin(45,4) = TU/AT   geeft  0,712... = TU/7,648...  dus  TU = 5,445...
De afstand van P tot AB is 11,89 - 6,40 = 5,49
TU is kleiner dan 5,49 dus de bal is buiten de rechthoek PQDR op de grond gekomen.
   
10. Begin met y = x3
Vervang x door  (x - 2),  dat geeft  y = (x - 2)3  en dat is een translatie 2 naar rechts
Vervang vervolgens x door 0,5x;   dat geeft de gevraagde functie, en dat is een vermenigvuldiging t.o.v. de y-as met factor 2.

OF:

Begin met y = x3
Vervang x door 0,5x,  dat geeft  y = (0,5x)3  en dat is een vermenigvuldiging t.o.v. de y-as met factor 2.
Vervang vervolgens x door  (x - 4), dat geeft  y = (0,5(x - 4))3 = (0,5x - 2)3  en dat is een translatie 4 naar rechts.

   
11. snijpunt x-as is y = 0
(0,5x - 2)3 = 0
0,5x - 2 = 0
x = 4.

Hoe groot is de helling bij x = 4?  Dat is de afgeleide.
y ' = 3 • (0,5x - 2)2 • 0,5     (die 0,5 komt van de kettingregel)
x = 4  geeft  y '= 3 • 02 • 0,5  = 0
Helling nul betekent dat de raaklijn in A horizontaal is.
   
12. 0,5x - 2 = (0,5x - 2)3
Daar staat eigenlijk  p = p3   (noem  0,5x - 2) = p)
p - p3 = 0
p(1 - p2) = 0
p = 0  ∨  p2 = 1
p = 0  ∨  p = 1  ∨  p = -1
0,5x - 2 = 0  ∨  0,5x - 2 = 1  ∨  0,5x - 2 = -1
x = 4  ∨  x = 6  ∨  x = 2
x = 2  geeft  P = (2,  -1) 
x = 6  geeft  Q = (6, 1)
PQ = √((6 - 2)2 + (1 --1)2) = √20 = 2√5 ≈  4,47
   
13. Y1 = 1 + 2cos(2x + π/3)   (denk erom dat de GR op radialen staat)
Calc - zero  geeft  P(0.52..., 0) en Q(1.57..., 0) en R(3.66..., 0) en S(4.71..., 0)
PS = 4,71... - 0,52... = 4,19...
QR = 3,66... - 1,57... = 2,08...
De verhouding is a = 2

OF

Het kan ook algebraïsch:
1 + 2cos(2x + π/3) = 0
2cos(2x + π/3) = -1
cos(2x + π/3) = -0,5
2x + 1/3π = 2/3π  + k2π  ∨    2x + 1/3π = -2/3π + k2π
2x = 1/3π + k2π  ∨  2x = -π + k2π
x = 1/6π + kπ  ∨   x = -1/2π + kπ
Dat geeft de oplossingen    1/6π,  1/2π, 7/6π, 3/2π
De rest gaat als hierboven.
   
14. Plot de grafiek van g en lees via calc - minimum/maximum twee toppen (een maximum en een minimum) af.
Dat geeft  bijvoorbeeld  maximum(0.6369, 2.4175)  en  minimum (2.2077, -4.4175)

evenwichtslijn  (2,4175 - 4.4175)/2 = -1 = p
amplitude: 2,4175 - - 1 = 3,418 = q
halve periode is  2,2077 - 0,6369 = 1,5708  dus de periode is 3,1415...  dus  r = 2π/3,1415... = 2 = r
beginpunt is in het maximum,  dus  s = 0,637
   
15.

   
16. A = 1000 en K = 7,85  (dat is het kleinste getal dat wordt afgerond naar 7,9)
Als D > 200 geldt de tweede formule:
7,85 = log(1000) +  3 • log(D) - 3,38
7,85 = 3 + 3 • logD - 3,38
3 • logD = 8,23
logD = 2,74333...
D = 102,74333.. = 553,77498....
De oppervlakte is  π • (553,77498...)2 = 963421,9557 km2  ≈ 963000 km2
   
17. K = log(A) + 1,6 • log(D) - 0,15  
K = log(A) + log(D1,6) + log(10-0,15)
K = log(A) + log(D1,6 + log(0,708)
K = log(A • D1,6 • 0,708)
 p = 0,71  en  q = 1,6
   
18. MA staat loodrecht op l
l heeft rc = 0,5  dus MA heeft rc -2
y = -2x + b moet door  M(-1,3)  gaan en dat geeft  b = 1
MA is de lijn  y = -2x + 1
A is het snijpunt van MA met l:  -2x + 1 = 0,5x - 1,5
2,5x = 2,5  dus  xA = 1
A is dan het punt  (1, -1)
De straal van de cirkel is MA = √((-1-1)2 + (3 - - 1)2) = √20
Omdat MABC een vierkant is  (MB = straal cirkel, en alle hoeken 90º)  is ook AC = BC = √20
Het gekromde deel is een kwartcirkel, dus heeft lengte  0,25 • 2π√20
Totale omtrek is  2√20 + 0,25 • 2π√20  ≈ 15,97